基于PSO与模糊PI控制结合的最大风能捕获研究

任志玲 杨永伟 孙雪飞

(辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125105)

0 引 言

风能是一种安全、清洁，无污染的能源。目前全世界约有75个国家拥有商用风力发电装置，其中22个国家使用的风力发电机装机容量已超过1千兆瓦级。为了实现风能的最大捕获，学者们提出了许多的控制方法，如文献[1]中将PI与SMC的结合，模型预测控制(MPC)简化计算，并将模糊控制器嵌入模型参考自适应控制框架，但由于风速的突变并不能达到功率实时跟踪。文献[2]中将模糊模型和神经网络相结合，对变速风力发电机的MPPT进行了研究，虽实现了风能的捕获，但风能利用系数较低。文献[3]中介绍了前馈气动力矩控制器(ATF)跟踪最优发电机转速，但是跟踪效果并不佳。文献[4]中考虑了范德霍文风模型分别针对高、低频设计了LQG控制器和PI控制器，但是转矩出现波动较大。文献[5]提出了一种基于永磁同步发电机爬山搜索(HCS)的Wilcoxon径向基函数网络MPPT策略，但是步长的选取需要经过多次尝试，功率和转矩变化响应时间较长。本文提出了一种基于粒子群优化(PSO)算法和最优模糊PI控制器，以最大限度地实现风能捕获。根据不同风速下粒子群算法对低负荷区域的模糊隶属函数进行调整，利用增益同步控制器得到各风速优化的PI增益，该PI控制器保证了最佳叶尖比。将该策略应用于5 MW风力机中，并与ATF和CMPPT两种控制策略进行参数比较，实验结果表明本策略具有实时跟踪风速变化引起的转速、转矩和功率的变化，在低负荷区域具有明显跟踪、响应快等特点。

1 风力机模型

图1表示风力发电系统的简易模型图，风速吹动风力机旋转获得的直接功率数学模型为：

Pv=0.5ρAv3

(1)

式中：A表示风扫过风轮的有效面积，v表示风速，ρ表示空气密度,一般取1.225 kg/m2。

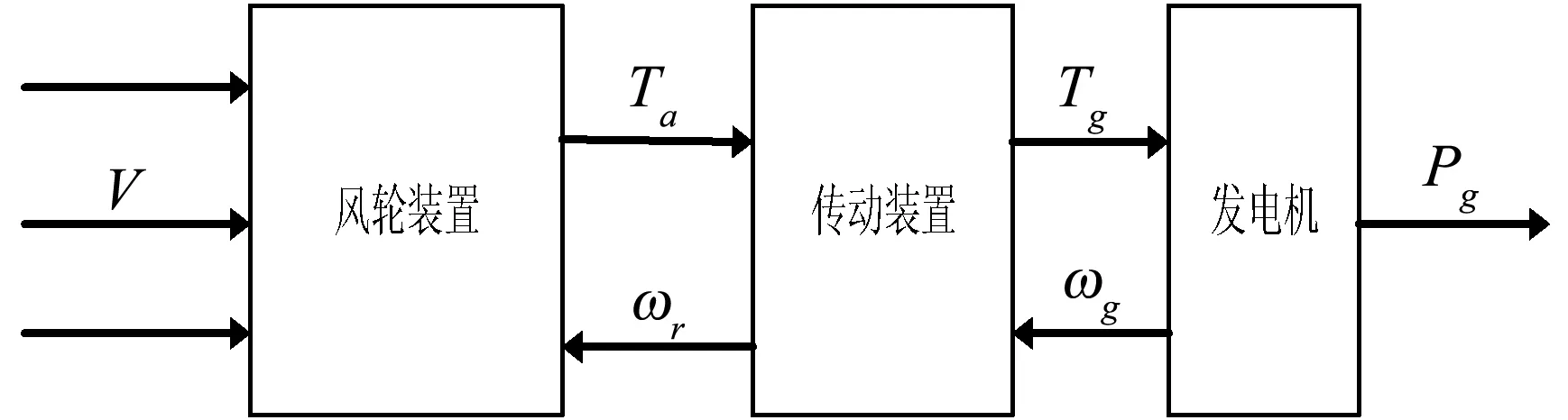
图1 风力发电系统框图

叶尖比的表达式为：

(2)

式中：ωr表示风轮角速度,R表示风力机的半径。

为了表示实际风能捕获的效率，引入风能利用CP，最大风能利用系数Cp采用如下表达式：

(3)

根据式(3)得到图2所示的风能利用系数曲线图。

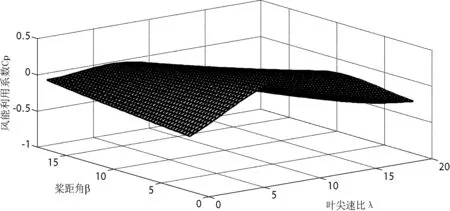
图2 最大风能利用系数曲线

风力机捕获的功率、转矩方程为：

(4)

式中：Pa表示风力机的输出功率，Ta表示风力机产生的转矩，ωr表示风力机角速度。

根据图3得到传动数学模型[6]：

(5)

式中：θr、θls、ωls、θg分别为转子侧偏差角、变速箱侧偏差角、低速轴偏差角、发电机侧偏差角；Ta、Tls、Ths、Tg分别表示风轮转矩、低速轴转矩、高速轴转矩、发电机的力矩；风力机传动比n：

(6)

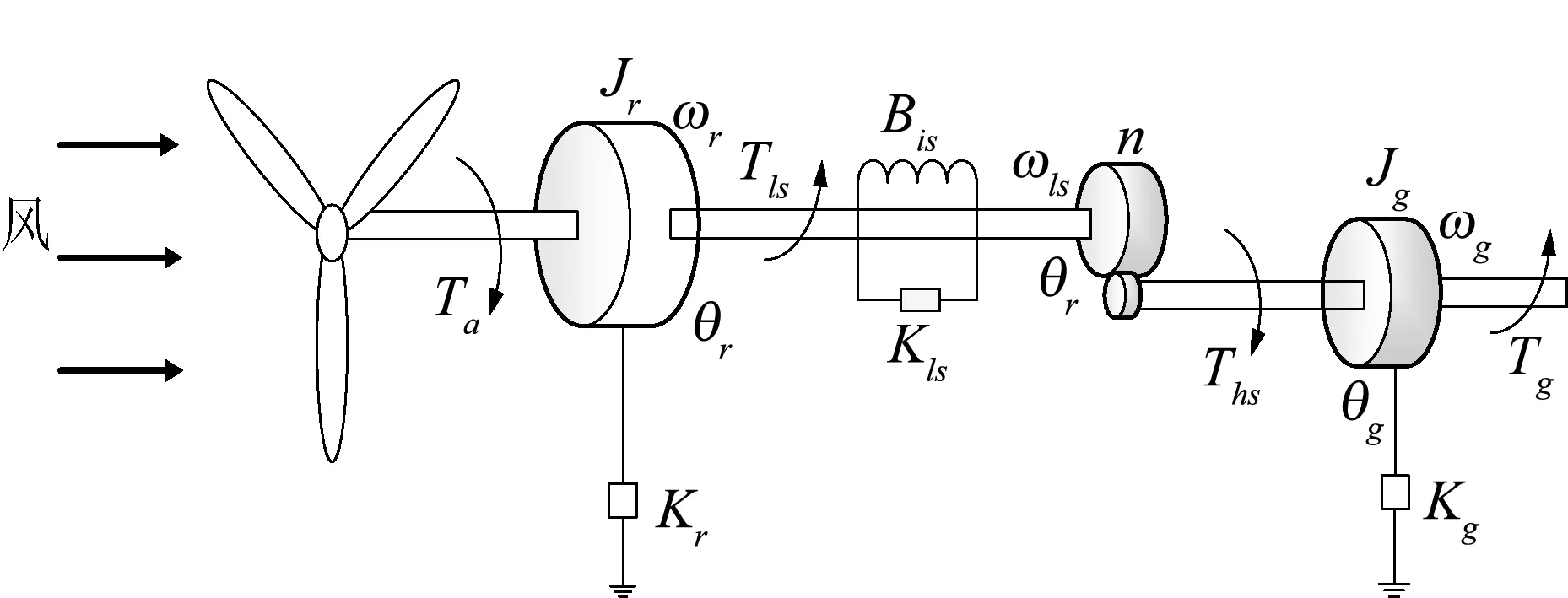
图3 二质量传动模型

文献[6]中转矩表达式：

(7)

从图2可以看出当叶片与风向正交(桨距角β为00)，最佳叶尖比λopt为7.55时Cp最大，利用最大风能利用系数Cp(max)曲线实现最大风能捕获。为保持λopt，此时应根据速度控制器调节转子速度。利用传统最大功率跟踪(简称CMPPT)控制策略实现上最大风能的捕获[7]，电磁转矩计算公式为：

(8)

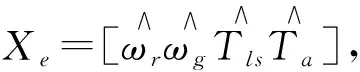
(9)

上述提出的方法称为前馈空气转矩控制器(ATF),其中Kc是为减小稳态误差而选择的参数。

2 最优模糊PI控制设计

2.1 粒子群算法(PSO)

粒子群优化算法(PSO)是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法，它提供了一种基于种群的搜索过程，其中的个体称为粒子，随着时间而改变它们的位置(状态)。在粒子群优化系统中，相当于粒子在多维搜索空间中飞行，在飞行过程中，每个粒子根据自己的经验和相邻粒子的位置来调整最佳的位置。在粒子群算法中，每个粒子都有一个速度和位置，相应的方程描述如下：

vi(k+1)=vi(k)+γ1i(Pi-xi(k))+γ2i(G-xi(k))

(10)

xi(k+1)=xi(k)+vi(k+1)

(11)

式中：i为粒子数，k为离散时间指数，vi为粒子的速度，xi为粒子的位置，Pi为粒子的最佳位置(全局最佳)，G为种群(全局最佳)的最佳位置，γ1i和γ2i为粒子在区间[0,1]中的自由随机数。在模拟中采用下列的迭代速度方程：

vi(k+1)=φ(k)vi(k)+α1[γ1i(Pi-xi(k))]+

α2[γ2i(G-xi(k))]

(12)

式中：φ(k)是惯性函数，α1和α2为加速度常数。在本文中使用线性递减策略，即最初的大惯性权重0.9线性地减少到0.1,相应的表达式如下：

(13)

式中：NT是执行算法的最大时间步数，φ(0)是初始惯性权重，φ(NT)是后惯性权重。

粒子群算法的步骤算法如下：

步骤1初始化粒子群并随机化每个粒子的位置和速度(xi,vi;i=1,…,M)。

步骤2计算每个粒子的适应度函数(y(i)=适应度(xi))。

步骤3初始化每个Pi和G,Pi0=yi,G=min(Pi0),i=1,2,…,M。

步骤4使用动态惯性权重更新粒子的速度，利用式(11)更新粒子的位置，并通过速度来控制，如下所示：

(14)

步骤5更新Pi和G;Pi=yi-new和G=min(Pi-new)。

步骤6如果不满足结束条件转到步骤4继续循环；否则，停止并返回参数G。

2.2 模糊PI控制设计

本文采用图4所示的二阶模糊控控制器，包括输入数据、模糊推理、清晰化、控制作用对象等部分。如果对隶属度函数进行优化调整可以达到较好的控制效果，则利用智能优化控制方法实现这个目标[9-13]；通过输入e和ec，经过模糊归一化，模糊推理，清晰化以后作用于控制对象，其中r表示输入，y表示输出。

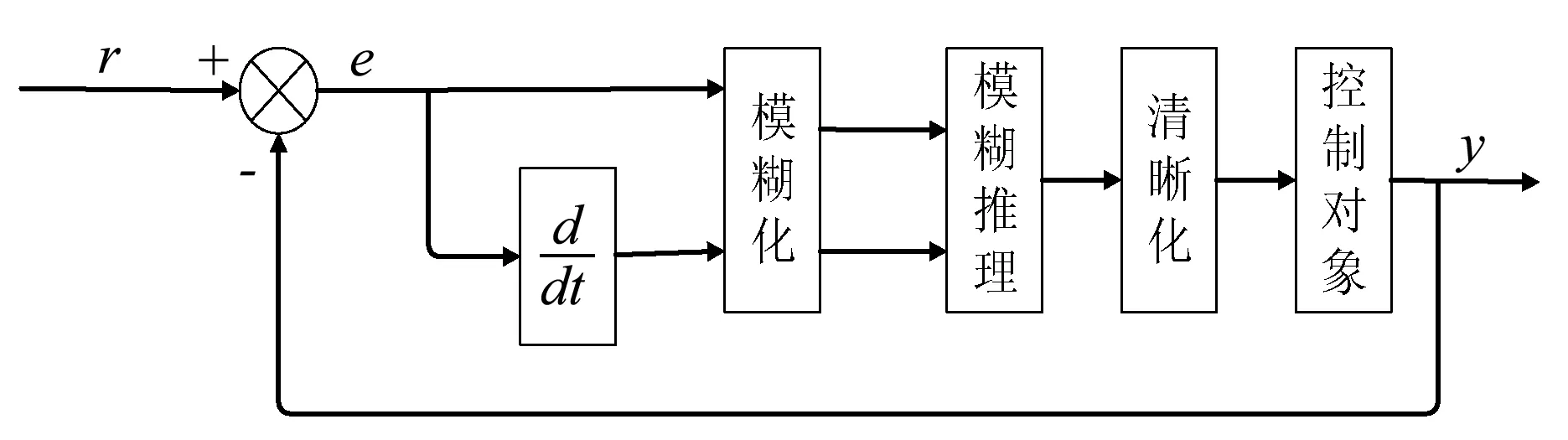
图4 二阶模糊控制器

从系统的稳定性响应速度、超调量等方面考虑：比例系数kp可以加快系统的响应速度，提高系统的调节精度；kp越大系统响应越快，但容易产生超调，甚至不稳定；较小时降低精度。积分系数ki的作用为消除系统静态误差。

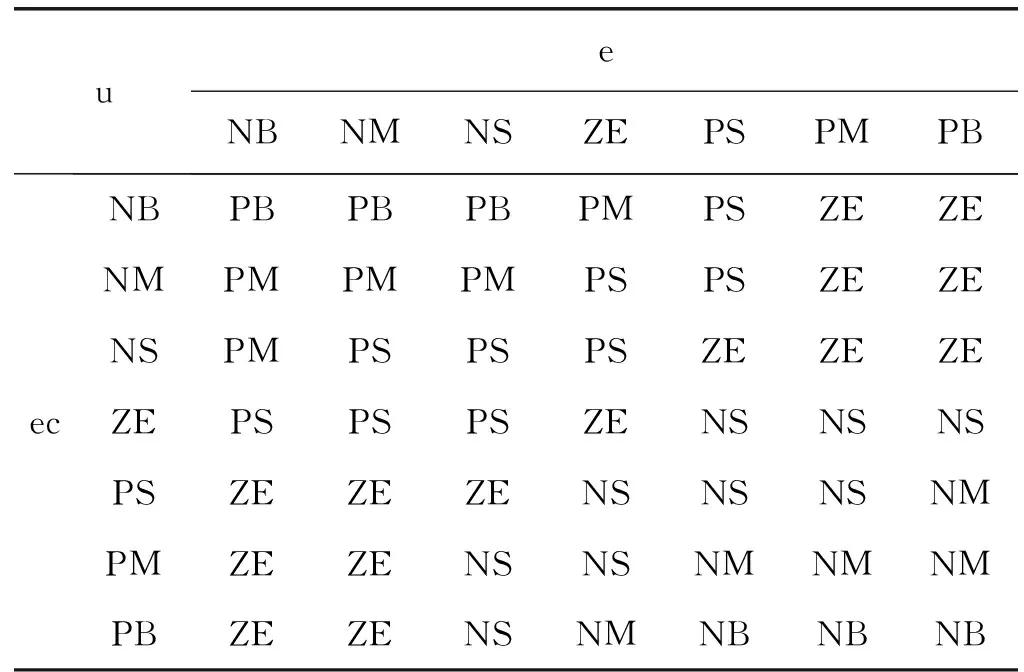
系统误差e和误差变化率ec论域为[-6,6],kp论域为[-2,2],ki论域为[-1,1],隶属度函数采用三角型函数，模糊子集均为{NB,NM,NS,ZE,PS,PM,PB},去模糊法为去重心法。根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计PI参数的模糊矩阵表，如表1、表2所示，并查出修正参数带入下式计算：

(15)

表2 ki模糊规则表

3 控制原理分析

本文提出的基于PSO群算法的最优模糊PI控制器对任意风速剖面都能实现风能的最大捕获。该方法分为两个阶段,如图5、图6所示。

图5 第一阶段(PSO控制)

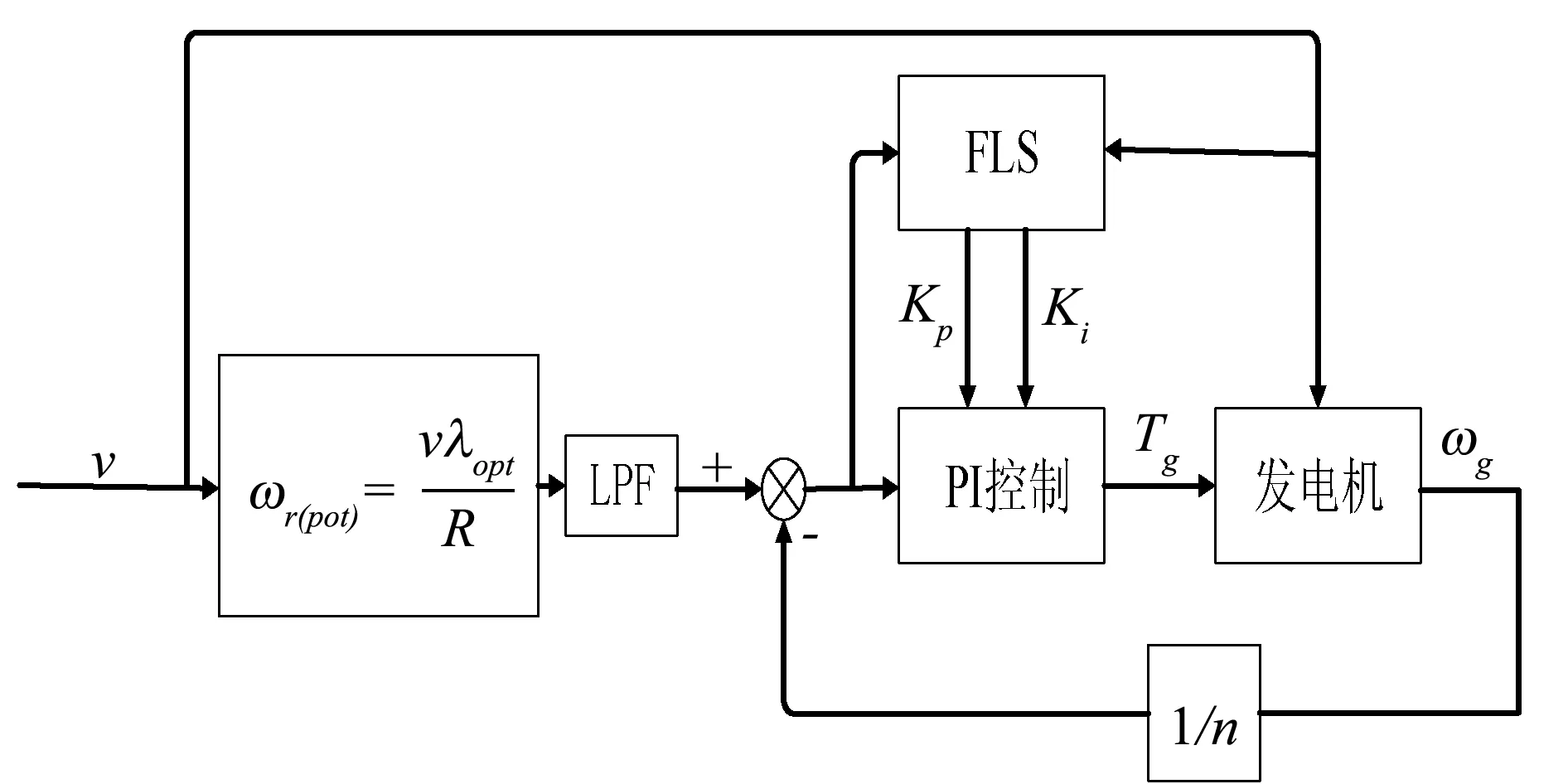
图6 第二阶段(模糊PI控制)

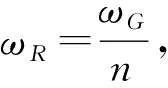
(16)

式中：s是Laplace变量因子，本文α选取0.01。

4 仿真结果分析

将本策略提出的控制器应用于一个5 MW风力机模型，在MATLAB/Simiulink仿真软件中设置参数，相关参数设置如表3、表4所示。表5为不同风速下采用粒子群优化后的Kp、Ki参数。

表3 5 MW风力机参数

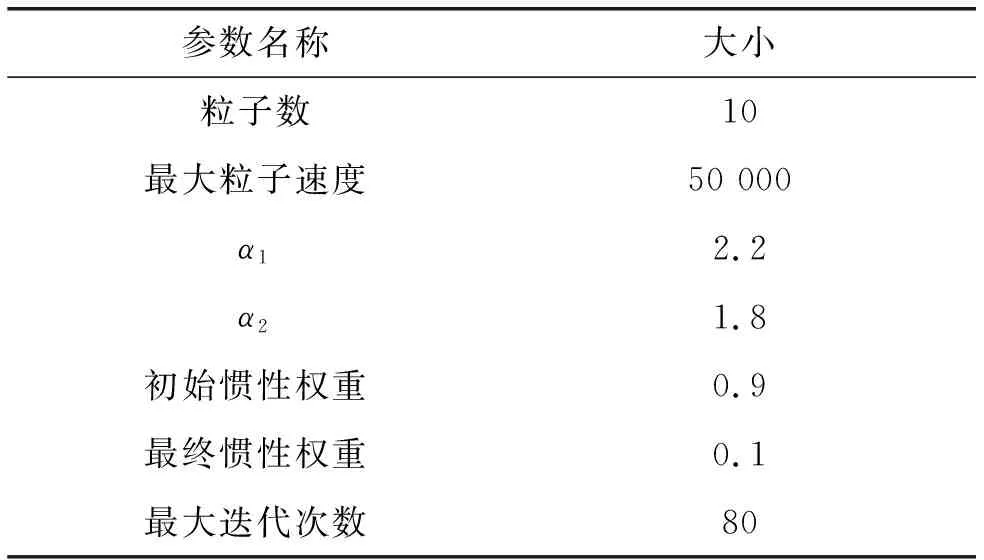
表4 PSO算法参数

表5 PSO算法优化后的Kp、Ki

为便于分析，设定仿真时间为300 s，采用图7所示的组合风速进行模拟，运行仿真得到与CMPPT和ATF控制策略的比较结果如图8-图11所示。

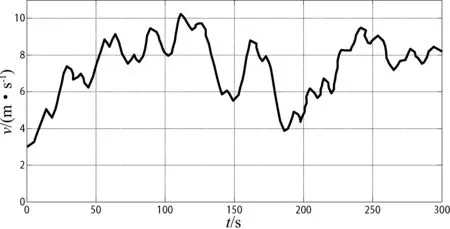
图7 模拟风速曲线

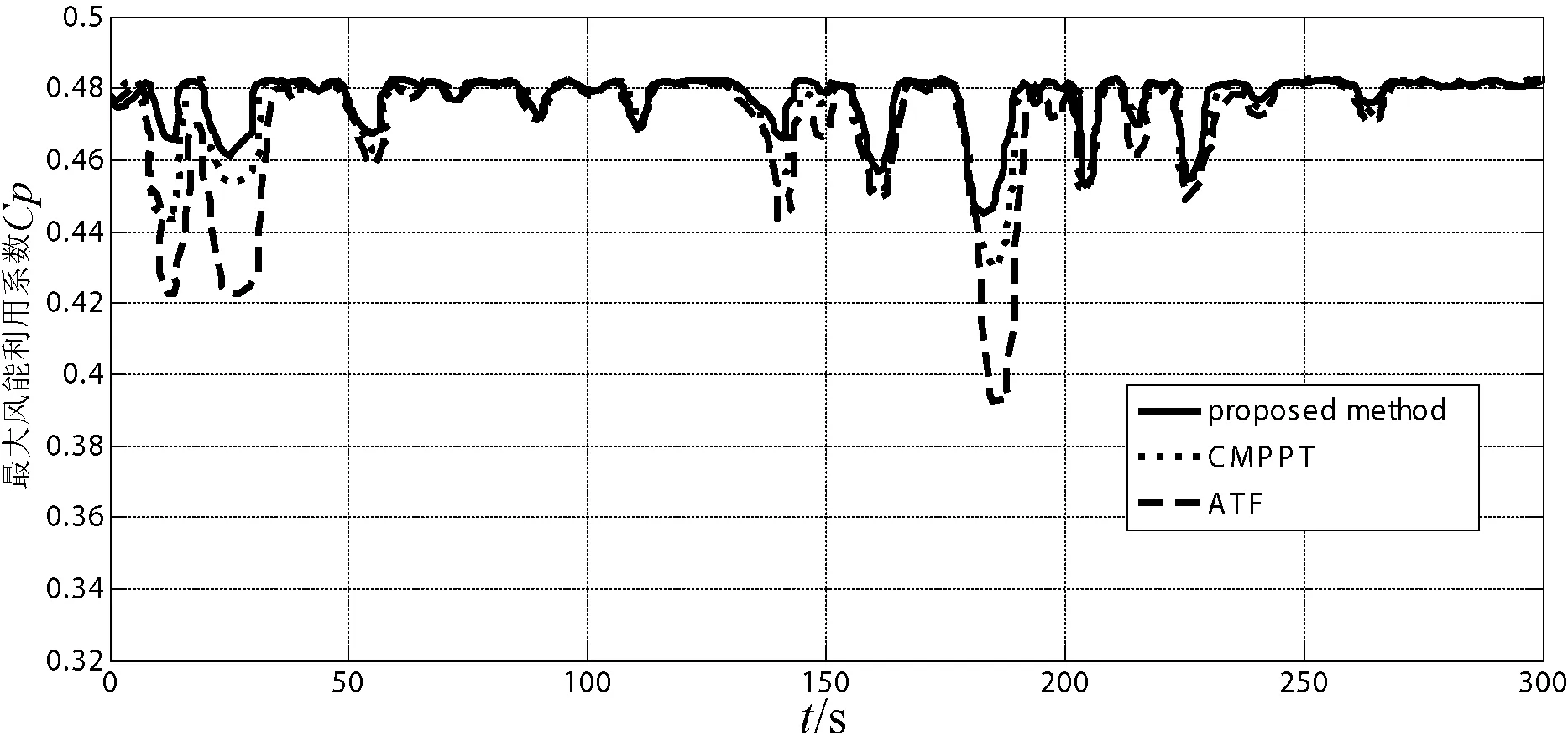
图8 三种策略下的Cp比较

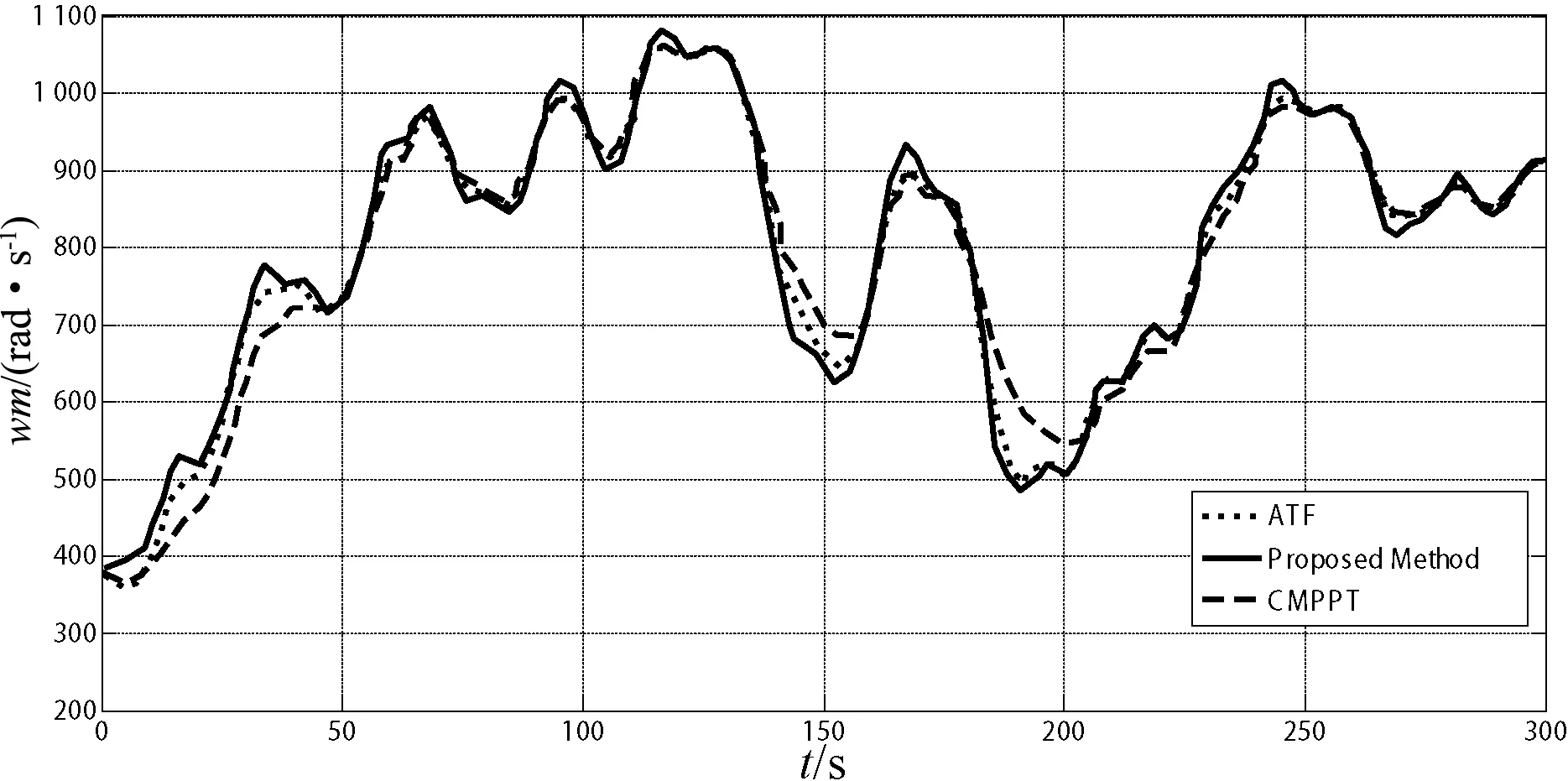
图9 不同策略下的转速比较

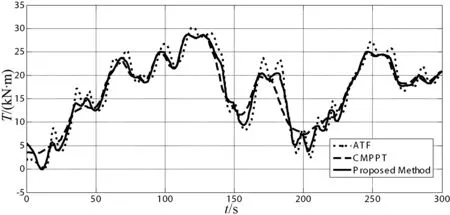
图10 不同方法的发电机转矩比较

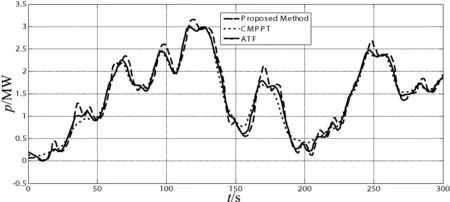
图11 不同方法的功率比较

从图7显示的模拟风速曲线可以看出风速是非线性运行时变，图8显示了不同方法的风能利用系数，风力机的最大风能利用系数Cp(max)为0.482。从图9中可以看出本文提出的方法能够比传统方法能更好地跟踪转速。与传统方法相比，图10和图11显示的转矩和功率曲线图中本文所提出的转矩控制具有一定的抗扰动能力，而且能更好地跟踪风速变化，系统响应时间较快，且转矩抖动幅度小。

为了比较不同方法的风能捕获效率或功率；使用统计学方法评估均值：

(17)

式中：ψ(t)可以是P(T)或CP(T)(即输出功率或风能利用系数)。根据评估均值J的大小可以看出，在一定时间内J越大越好。表6显示了三种不同策略下的(本文方法、CMPPT和ATF)比较分析结果，其中：Pout(avg)表示一定时间内的平均输出功率；Cp(avg)表示一定时间内最大风能利用系数的平均值。由表6可见，本文提出的方法具有较好的功率捕获性能。

表6 不同策略下的J比较

5 结 语

本文提出了一种基于粒子群算法和模糊PI结合的最优转矩控制器，用于实现低风速时的最大风能捕获。利用粒子群算法求出了不同风速下的最优PI增益，利用最优PI增益进行模糊PI控制优化参数；为了减小风速变化引起的转矩波动，采用低通滤波器。与另外的CMPPT、ATF两种控制策略相比，本文提出的策略能较好地跟踪转速、功率和转矩，转矩波动小。为证明结果的可靠性，采用统计学方法分析本文提出的策略，结果显示本文策略能实现风能的最大捕获结果，具有明显的优越性。