浅谈高中数学如何培养学生解决问题的能力

文/广州市海珠外国语实验中学 邱水金

培养学生解决数学问题的能力是数学教学的核心问题，数学教学的根本目的是培养学生的数学意识,培养数学知识的自我更新、自我增长能力、创新能力，能够用数学的眼光看待事物，能够应用所学的数学知识去解决一些实际问题。

一、解决数学问题能力的组成

1.审题能力

审题是对题目条件和结论进行全面的认识，对与条件和结论有关的信息进行分析研究，它是分析问题和解决问题的前提。审题能力主要指： （1）充分理解题意，把握题目本质特征； （2）分析和发现题目的隐含条件； （3）化简、转化已知和结论的能力； （4）快捷、准确地掌握题目的数形特征。对题目所给的条件和结论进行转化和发现隐含条件是解决问题至关重要的因素。

2.综合应用能力

高中数学知识包括函数、不等式、数列、三角函数、复数、立体几何、解析几何等内容；数学思想包括数形结合、函数与方程思想、分类与讨论和等价转化等；数学方法包括待定系数法、换元法、数学归纳法、反证法、配方法等基本方法。只有理解和掌握数学基本知识、思想、方法，才能解决高中数学中的一些基本问题，而合理选择和应用知识、思想、方法可以使问题解决得更迅速、顺畅。

例： 设 C1， C2， …， Cn， …是坐标平面上的一列圆，它们的圆心都在x轴的正半轴上，且都与直线相切，对每一个正整数n，圆Cn都与圆Cn+1相互外切，以rn表示Cn的半径，已知 {rn}为递增数列。

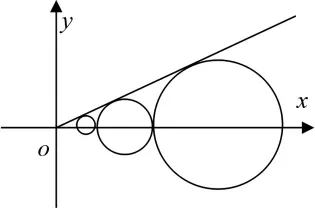
(Ⅰ)证明： {rn}为等比数列；

（Ⅱ）设r1=1，求数列的前n项和。

分析：本题考查等比数列的基本知识，利用错位相减法求和等基本方法，考察抽象概括能力以及推理论证能力。

（1）求直线倾斜角的正弦，设 Cn的圆心为 （λn， 0）， 得 λn=2rn，同理得λn+1=2rn+1，结合两圆相切得圆心距与半径间的关系，得两圆半径之间的关系，即 {rn}中rn+1与的关系，证明 {rn}为等比数列；（2） 利用 （1） 的结论求 {rn}的通项公式，代入数列然后用错位相减法求和.

对于数列与几何图形相结合的问题，通常利用几何知识，并结合图形，得出关于数列相邻项an与an+1之间的关系，然后根据这个递推关系，结合所求内容变形，得出通项公式或其他所求结论。

3.数学建模能力

“数学建模”是运用数学思想、方法和知识解决实际问题的过程，已经成为不同层次数学教育重要的和基本的内容。近几年来，在高考数学试卷中，都涉及一些实际应用问题，这给学生的分析和解决问题的能力提出了挑战。而数学建模能力是解决实际应用问题的重要途径和核心。

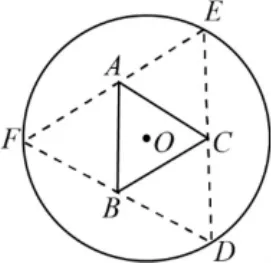
例： （2017年全国1卷）如图，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O，D、E、F为元O 上 的 点 ， △DBC， △ECA，△FAB分别是一BC，CA，AB为底边的等腰三角形，沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D，E，F重合，得到三棱锥。当△ABC的边长变化时，所得三棱锥体积 （单位：cm3）的最大值为______。

分析：本小题主要考查折叠问题、等边三角形的性质、导数等基础知识，考查数学建模能力、空间想象力、数学阅读能力及解决实际问题的能力。若学生能找出OG与BC的关系的这个关键，再利用体积公式，就不难找出自变量x与BC和DG的关系，从而就能建立数学模型。

在该题的解答中，这是一道较常见数学建模题，但学生若没有一定的数学建模能力，正确解决此题实属不易。若能建模，再利用导数这个工具就迎刃而解了。因此，建模能力是分析和解决问题能力不可缺少的一个组成部分。

二、培养学生解决数学问题能力的方法策略

1.重视基础知识，建立良好的数学认知结构

引导学生学会审题、解题，是日常教学中最基本也是最重要的一环，是最基本的，也是我们在现实教学中最容易忽视的环节。正如在新课程改革中提出 “淡化知识”，于是便又忽略必要的知识传授一样。而恰恰相反，只有给学生传授一定相应的知识，并引导学生掌握审题、解题的基本方法，经过反复训练，激发潜能，才可以形成能力，使学生的学习兴趣获得保持和发展，达到教是为了不教的教学目的，这正是授之以 “渔”的教学策略具体化的体现。在高三的复习中，特别是面对要用到好几个知识点才能解决的问题时，建立良好的数学认知结构尤为重要。

2.重视策略化知识，建构不同的知识点

高中数学知识面广，高考的范围大。从2017年考纲来看，旧的知识基本不变，新课标以能力立意，将知识、能力和素质融为一体，全面检测考生的数学素养，如何把数学的思想方法融入到教学中，把不同的知识点有机的结合起来，课程标准指出：数学的发展既有内在的动力，也有外在的动力，在高中数学的教学中，要注重数学的不同分支和不同内容之间的联系，数学与日常生活的联系，数学与其他学科的联系。我们只有在教学过程中不断地把这些思想和方法，用不同的题目训练学生，让学生理解和掌握了数学基本知识、基本思想和基本方法，才能解决高中数学中的一些基本问题，进而能合理地选择和运用知识、思想和方法，使问题解决得迅速、流畅，才能在高考中占有一席之地。

3.加强应用题的教学，培养学生从实际问题中概括数学问题

建模能力是解题者对各种能力的综合应用，它涉及文字理解能力，对实际的熟悉程度，对相关知识的掌握程度，良好的心理素质，创新精神和创造能力，以及观察、分析、综合、比较、概括等各种科学思维方法的综合应用。为此，在应用教学中，师生应组成 “共同体”，在老师的点拨指导下，以小组为单位开展建模活动，提高学生独立工作和相互合作的能力，教师重点在科学的思维方法上给予点拨和总结。让学生培养善于从实际问题中识别出数学模式，引导学生总结、归纳各种应用题的数学模型，这样学生才能有的放矢，合理运用数学思想和方法分析解决实际问题。

4.积极反思，查缺补漏，确保解题的合理性和正确性

解数学题时，有时由于审题不确，概念不清，忽视条件，套用相近知识，考虑不周或计算出错，难免产生这样或那样的错误，即学生解数学题，不能保证一次性正确和完善。所以解题后，必须对解题过程进行回顾和评价，对结论的正确性和合理性进行验证，引导学生不断地对问题进行观察分析、归纳类比、抽象概括，对问题中所蕴含的数学方法、数学思想进行不断地思考并做出新的判断，让学生体会解题带来的乐趣，享受探究带来的成就感。长此以往，逐步养成学生独立思考、积极探究的习惯，这是学好数学的必要条件，更是以后进行分析和解决问题的基础。

总之，教学实践是一个复杂的过程，理论是不可能完全应用于实践中的，这就需要教师在今后的教学实践中大胆尝试，细心领会，发现问题，积极寻求解决问题的方法，培养提高学生解决问题的能力。