基于CDbw和人工蜂群优化的密度峰值聚类算法
姜建华, 吴 迪, 郝德浩, 王丽敏, 张永刚, 李克勤
(1. 吉林财经大学 数据科学系, 吉林省互联网金融重点实验室, 长春 130117;2. 吉林大学 符号计算与知识工程教育部重点实验室, 长春 130012;3. 纽约州立大学 计算机系, 美国 纽约 12561)
聚类分析可在没有任何先验信息下对数据进行分析, 识别数据空间的潜在结构[1], 广泛应用于模式识别和市场研究等领域[2]. Hartigan等[3]提出的基于欧氏距离的K-means聚类算法, 由于算法简单、 高效而被广泛使用; Frey等[4]提出了近邻传播(affinity propagation, AP)算法, 并应用于图像识别[5]中; Rodriguez等[6]提出了一种基于密度峰值的聚类(DPC)算法, 因其能快速发现任意形状数据集的密度峰值点, 并能高效进行样本分配和离群点剔除, 已引起广泛关注[7-8], 但该算法对于类簇间数据点的识别与分类有待商榷.
本文以DPC算法为基础, 提出一种基于人工蜂群与CDbw聚类指标优化的密度峰值(BeeDPC)算法, 继承了DPC算法在聚类中心点自动识别、 自动聚合的优势, 通过计算数据点到近邻的最高密度点和次高密度点距离之间的关系, 提升类簇间数据点类别判断决策的科学性.
1 BeeDPC算法
DPC算法的核心是通过聚类中心点主动吸附与其距离较近且密度更小的点, 实现任意分布数据集的聚类, 但其存在一定的局限: 1)dc值的选取极大影响聚类结果; 2) 相邻聚类间的点存在类别判断不合理问题; 3) 聚类结果依赖于已完成类别判断的高密度点, 一旦存在错误类别判断的高密度点即直接导致所跟随的低密度数据点的误判, 并产生连带效应.
图1为R15数据集的密度峰值聚类结果. 由图1可见, 当dc=0.728 8时, 聚类结果接近合理聚类结果(图1(A)); 当dc=1.419 6时, 聚类结果不理想(图1(B)), 表现为在类簇间存在一定数量点的误判.

图1 R15数据集的密度峰值聚类结果Fig.1 Density peak clustering results of R15 data set
本文BeeDPC算法在充分继承DPC算法优势的基础上, 对其聚合原则做出相应调整, 以提高DPC算法对类簇间数据点的敏感度, 给出更合理的类簇间点聚合原则. BeeDPC算法步骤如下:
1) 计算数据点的密度并生成决策图.
首先计算数据点间的距离, 将降序排列后得到的截断距离作为dc值, 并计算各数据点密度. 第i个数据点的密度值为
(1)
其中dij表示第i个数据点到第j个数据点间的距离, 当dij-dc<0时,χ(dij-dc)=1; 否则,χ(dij-dc)=0. 第i个数据点到全部比其密度值高点的距离最小值为
(2)
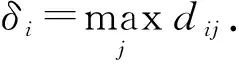
2) 按聚类原则对数据点初步聚类.
BeeDPC算法在聚类原则上借鉴三角稳定性思想, 在每个数据点聚类前, 不仅简单考虑与该点距离最小的相对高密度值点(nneigh1), 还考虑与该点距离次小的相对高密度值点(nneigh2). 当nneigh1和nneigh2属同一类时, 可认为该数据点有较明确的聚类归属; 当nneigh1和nneigh2为不同类时, 认为该数据点的聚类结果可能存在由其特殊位置导致的争议情形, 它既可与nneigh1属同一类, 也可与nneigh2属同一类.
3) 识别类簇间数据点.
经过对数据点的初步分类, 所有数据点主要分为两类: 已明确类别判定数据点集和类簇间未判定数据点集. 在聚合操作上, 对已明确类别判定数据点集使用DPC方法进行直接聚类, 但对类簇间未判定数据集则需进行二次类别判定.
第i个数据点最小距离与次小距离的差值为
γi=|Disti,nneigh1-Disti,nneigh2|,
(3)
其中: Disti,nneigh1表示第i个数据点到与其最近的高密度值点nneigh1的距离; Disti,nneigh2表示第i个数据点到与其次近的高密度值点nneigh2的距离. 对于γi的不同取值, 有:
① 当γi>dc时, 认为第i个数据点到nneigh1和nneigh2之间的距离有显著性差别, 则该数据点处于距离nneigh1和nneigh2中较小距离的聚类边缘位置, 故该数据点的所属类簇应与距离较近的聚类一致;
② 当γi 4) 寻找所有类簇间数据点可能的所属类簇标号. 在使用蜂群算法寻优前, 首先要确定类簇间数据点最可能的所属类簇标号. 对于每个类簇间数据点, 根据其与nneigh1和nneigh2的已知关系可确定其最可能的所属类簇标号. ① 当nneigh1和nneigh2所处类簇标号均已知时, 直接记录两个类簇标号作为该数据点的可能类簇集; ② 当nneigh1和nneigh2中任意一个所处类簇标号未知时, 计算该数据点到各类簇中心点距离, 选出距离最近的类簇标号和另一个已知类簇标号作为该数据点的可能类簇集; ③ 当nneigh1和nneigh2的所处类簇标号均未知时, 计算该数据点到各类簇中心点距离, 选出距离最近的类簇标号和距离次近的类簇标号作为该数据点的可能类簇集. 5) 以CDbw值为目标函数, 使用人工蜂群算法对类簇间数据点进行二次类别判定. 基于聚类间的紧密度和分离度计算的分类评价指标(CDbw), 可有效测量任意分布数据集的分类效果. 蜂群算法是模拟蜜蜂采蜜行为的优化方法[9], Karaboga等[10]研究表明, 蜂群算法可广泛应用于特征选择[11]、 参数优化[12]、 作业调度[13]和旅行推销员[14]等问题. 识别待分类中数据点的归属问题也可视为一个优化问题, 针对数据点的不同取值, 使用以CDbw为目标函数的人工蜂群算法对待分类数据点的所属类簇标号求解可较好地解决该问题. CDbw主要依赖簇间的分离程度和簇内的紧密程度: (4) (5) 整体类簇间的密度为 (6) (7) 当分类效果较好时, 不同类簇间的距离更远, 密度值也相对较小; 反之, 当分类效果较差时, 不同类簇间的距离相对较小, 密度值相对较高. 相对类簇内密度为 (8) (9) 其中:s为伸缩系数; stdev为数据点的密度标准差; cardinality(vij)表示类簇间密度值, 计算公式为 (10) 式中:vij为对每个类簇内数据点使用伸缩系数s调整后的数据点;xl为类簇内的数据点;ni为类簇内数据点的数目. 类簇C的紧密度为 (11) 为了抵消簇内紧密程度和类簇形状、 位置间的相互影响, 根据伸缩系数s引入ns作为影响因子, 本文设ns=8. 在考虑到类簇内紧密度的基础上计算出的类簇间分离度为 (12) 计算聚类结果的CDbw值为 CDbw(C)=Cohesion(C)·SC(C),c>1. (13) 由考虑到类簇内紧密度的类簇间分离度和类簇内紧密度组成CDbw评价系数. 分类效果越好, CDbw值越大. 本文提出以CDbw为目标函数的蜂群算法, 针对每次类簇间数据点的聚类结果, 根据CDbw取值寻优求解, 最终得到最优解, 即类簇间数据点的最佳聚类结果. 6) 反复评估, 直至完成全部数据点的聚类. 将得到的可明确分类数据点的聚类结果与类簇间数据点的聚类结果整合出最终结果, 并用轮廓系数(Sil)和F值评价聚类结果. 为了测试BeeDPC聚类算法的有效性和稳定性, 在数据集上, 选取部分已知数据集和自定义二维数据集作为输入数据; 在聚类算法上, 将本文算法与K-means,AP和DPC等算法进行对比. 选用的测试数据集参数列于表1. 表1 测试数据集参数Table 1 Parameters of testing data sets BeeDPC算法克服了DPC算法在类簇间数据点聚类不合理的缺陷. 在DPC算法中, 聚类结果极大地依赖dc的取值, 导致许多类簇间数据点的聚类极不合理, BeeDPC算法较好地解决了该问题. 图2为自动识别不同数据集中类簇间数据点的结果, 其中: (A),(B),(C)为已知数据集类簇间数据点的识别结果; (D),(E),(F),(G)为自定义数据集类簇间数据点的识别结果. 图2 自动识别不同数据集中类簇间数据点的结果Fig.2 Results of automatic identification of data points between clusters of different data sets BeeDPC和DPC算法在识别任意形状数据集的类簇中心点和类簇数目上都有显著效果. 凭借原DPC算法的优势, 考虑到各点的密度和点间距离关系, 可清晰地确定数据集的类簇中心点和类簇数目. 在决策图中, 无论是已知数据集(Flame), 还是自定义数据集, 相比于其他数据点, 类簇中心点在决策图中都较凸显. 显然, 比预设定类簇个数的K-means算法和偏向参数的AP算法更有优势, 因其可容易确定类簇数目及中心点. BeeDPC和DPC算法在处理不同形状、 大小的数据集都有显著效果. 已知数据集Aggregation具有大小、 形状不同的7个类簇, 由K-means,AP,DPC和BeeDPC算法聚合的结果如图3所示. 图3 Aggregation数据集的聚合效果Fig.3 Clustering effets of Aggregation data set 轮廓系数(Sil)是结合内聚度和分离度的评价方式, 常用于表示评估聚合效果, 定义如下: (14) 其中:a(t)表示向量t到其簇内其他点的距离;b(t)表示向量t到其他簇内各点的平均距离. 轮廓系数(Sil)的值域为[-1,1], 值越大表明分类结果的内聚度和分离度都相对较优, 聚合效果相对较好. 本文选用K-means,AP,DPC聚类算法与BeeDPC算法分别针对3个已知数据集(Flame,Aggregation,R15)进行对比实验, 实验结果列于表2. 由表2可见, 本文算法的聚类效果整体最优. 表2 不同数据集聚类结果的Sil值Table 2 Sil values of clustering results for different data sets 本文提出的BeeDPC算法是以DPC算法的假设为基础, 但聚类原则上与DPC算法截然不同. BeeDPC算法在对数据点聚类的同时更注重类簇间数据点的聚合处理. 本文对已知的数据集和特殊的自定义数据集都进行了测试, 并与K-means,AP,DPC三种聚类方法进行了对比. 对比结果表明, 本文方法主要有以下优点: 1) 自动识别类簇间数据点. 由于DPC算法对待分类数据点的类别判断仅依据单个已确定的点, 一旦存在某个数据点的判断不合理就会极大影响其余待分类数据点的聚合效果. 因此, 本文将三角形稳定性原理的思想引入DPC算法中, 同时考虑待分类数据点及其与最高密度点、 次高密度点之间距离的相互关系, 实现类簇间数据点的识别. 特别地, 所提出的BeeDPC算法是在对普通数据点聚类的同时可实现对类簇间数据点的识别. 2) 聚类类簇间数据点的合理性. 在聚类原则上, 本文摒弃了DPC算法的弊端, 同时引入最高密度点和次高密度点到待分类数据点的距离, 充分考虑三点之间距离相对关系所对应的不同情形, 针对数据点的不同特性使用不同的处理方法. 在对类簇间数据点处理时, 引入了优化算法----蜂群算法, 并以CDbw值为目标函数, 极大提高了对类簇间数据点所属类簇的科学聚类. 3) 处理任意分布的数据集. BeeDPC算法是对DPC算法在聚类原则上的进一步改进, 因此, 本文算法很好地保留了DPC算法的优势, 能处理任意形状及任意密度的数据集. 综上所述, 本文提出的BeeDPC算法在保留DPC自动识别类簇中心和可处理任意分布数据集优点的基础上, 引入三角形稳定性原理, 通过比较待分类数据点和最高密度数据点、 较高密度数据点三者距离上的相互关系, 得到类簇间数据点可能的聚类结果的集合, 使用以CDbw值为目标函数的蜂群算法求得类簇间数据点聚类的最优解, 得到全部数据点的聚类结果. 实验结果表明, BeeDPC算法对任意分布的数据集, 在类簇间数据点的识别和分类上都有较大优势.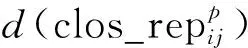

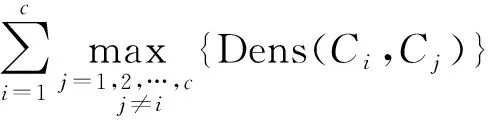
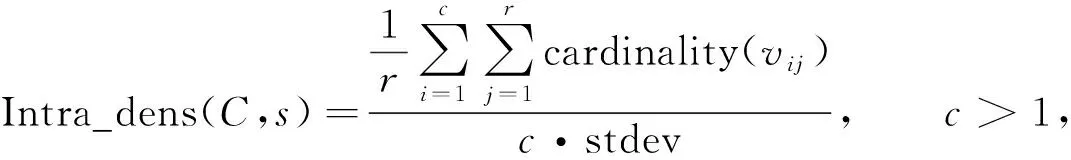
2 实验结果与分析

2.1 自动识别类簇间数据点

2.2 自动识别任意形状数据集的类簇中心点和类簇数目
2.3 处理不同形状和大小的数据集

2.4 分类效果评价

2.5 结果分析

