土壤初始含水率对微孔陶瓷渗灌入渗特性的影响
陈 玺,董爱红,赵 笑,蔡耀辉,张 林
(1.西北农林科技大学水利与建筑工程学院,陕西 咸阳 712100;2.西北农林科技大学水土保持研究所,陕西 咸阳 712100)
地下滴灌是目前应用最为广泛的地下灌溉技术,但其所用灌水器材质大多为塑料且工作水头较高,不利于可持续发展。而微孔陶瓷灌水器是以石英砂、滑石粉和硅溶胶等原料通过一定的工艺烧结制备而成的新型地下灌水器[1,2],与常规滴灌灌水器相比,具有节能环保等优点,适宜在干旱和半干旱地区推广应用[3-6]。无压灌溉作为一种新型的灌水方法,其可行性已通过相关研究[7-9]得到了验证。赵伟霞等研究[10]发现无压灌溉的累计入渗量与时间呈幂指数关系,土壤入渗率趋于零是无压灌溉过程结束的标志。无压灌溉过程中,各层或各深度范围内含水率变化趋势相近,湿润体内固定点处的含水率在灌水过程中几乎不发生变化,灌溉水量的增加只是用来扩大湿润体的大小[11]。无压条件下微孔陶瓷渗灌是以土水势为驱动力进行的一种主动灌溉。在生产实践中,由于气候和灌溉制度的不同,往往需要在不同的土壤初始含水率条件下进行灌溉[12]。土壤初始含水率是对土壤基质势及湿润锋处的基质势梯度产生影响,从而影响土壤水分的入渗[13,14]。在对涌泉根灌和微润灌溉等[15,16]的研究中发现,土壤初始含水率对湿润锋的运移以及水分入渗均有较大影响,土壤初始含水率越大,水分扩散速度越快。因此土壤初始含水率是影响水分入渗的关键因素之一。目前针对微孔陶瓷渗灌入渗特性的研究,主要集中在工作压力、设计流量等系统参数上[1,17,18]。例如任改萍等[18]研究发现在微孔陶瓷灌水器灌溉过程中,决定土壤水分累计入渗量和初始入渗速率的关键因素是供水压力,并且在各供水压力水平下,微孔陶瓷渗灌形成的湿润体大小和含水率均能满足作物根系吸水需求。但对不同初始含水率条件下微孔陶瓷渗灌的入渗特性研究还较少。
本文以微孔陶瓷灌水器为研究对象,分析土壤初始含水率对其累计入渗量和湿润锋运移距离的影响,探明不同初始含水率条件下微孔陶瓷渗灌的入渗特性,以期为微孔陶瓷灌水器的设计及田间应用提供一定的科学依据。
1 材料与方法
1.1 试验装置及土壤
试验在西北农林科技大学旱区节水农业研究院灌溉水力学试验大厅进行。试验装置(见图1)由供水装置、土箱和微孔陶瓷灌水器组成。供水装置为能够提供恒定水头的马氏瓶,其横截面直径为10 cm,高度90 cm。试验土箱由有机玻璃制作,尺寸为45 cm×45 cm×75 cm(长×宽×高)。微孔陶瓷灌水器(见图2)是由西北农林科技大学中国旱区节水农业研究院自主研制,其结构为圆管形,尺寸为4 cm×2 cm×8 cm(外径×内径×高)。试验土壤取自陕西渭河三级阶地,将试验土壤风干、碾压、混合后过2 mm筛网后备用。土壤颗粒组成采用激光粒度分析仪(MS2000型,马尔文,英国)测定,其中黏粒23.14%、粉粒34.01%、砂粒42.85%。按国际制土壤质地分类标准,试验土壤属于黏壤土。
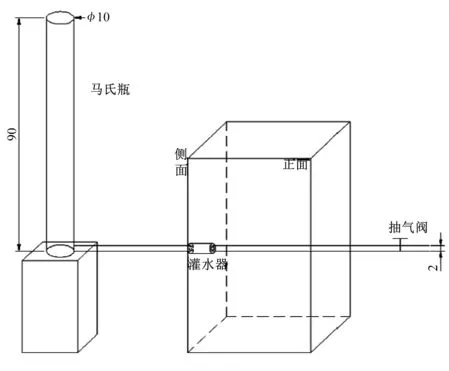
图1 试验装置示意图(单位:cm)Fig.1 Layout of the experimental platforms

图2 微孔陶瓷灌水器Fig.2 Porous ceramic emitter
1.2 试验方法及测定内容
试验土壤按设计干容重1.35 g/cm3分层装入土箱,每层5 cm,共填15层,为使土壤颗粒充分接触,两层之间进行打毛。土壤表面用塑料薄膜覆盖,防止土壤水分蒸发影响试验结果。微孔陶瓷灌水器水平放置埋于距土壤表面30 cm处,如图1所示。灌水器两端用管道连接,一端连接至马氏瓶,另一端尾部设有排气阀(试验开始时进行排气处理,从而使管道充满水)。马氏瓶出水口与水平放置的灌水器中心齐平,即灌水器工作水头为零。本试验通过采用土壤初始含水率的不同,分别为3%、9%、12%和15%,研究累计入渗量和湿润锋运移距离随入渗时间的变化。试验观测时间为50 h。累计入渗量通过观察马氏瓶的读数进行换算得出。试验结束后,以灌水器为中心通过尺子在土箱表面对所画湿润峰进行量测。选取图1中土箱正面的垂直向下和垂直向下的湿润峰运移距离和土箱侧面水平方向上的湿润峰运移距离,再对应所记录的时间,得出湿润锋运移距离随时间的变化。
2 结果与分析
2.1 土壤初始含水率对累计入渗量的影响
图3为不同初始含水率条件下累积入渗量随入渗时间的变化曲线。从图3可以看出,随着入渗时间的增加,累计入渗量的变化率逐渐减小。这是由于无压条件下,微孔陶瓷灌水器出流的驱动力为土水势,即累计入渗量随时间变化规律是由土水势决定[19]。开始入渗时土壤初始含水率较低,土壤水分主要受到土壤颗粒的吸力(最小值31 atm)和颗粒之间所形成孔隙的毛细管力(最小值0.3 atm)作用[19],此时基质吸力非常大,促进灌水器出流,故累计入渗量的变化率较大;随着时间的增大,灌水器附近一定范围内的土壤含水率高于田间持水率,土壤中的毛管悬着水达到最大,毛管力为0,此时基质吸力非常小,从而减缓了灌水器的出流,故随着入渗时间的增加,累计入渗量的变化率逐渐减小。同一时刻,土壤初始含水率越大,累计入渗量越小是因为土壤初始含水率越大,基质势越大即基质吸力越小,故累积入渗量越小。为定量分析累计入渗量随时间的变化关系,对数据进行拟合,结果见表1。

图3 不同土壤初始含水率下累积入渗量随时间的变化Fig.3 Changes of accumulative infiltration by time with different initial soil water contents

表1 不同初始含水率条件下累积入渗量随时间变化的拟合公式Tab.1 Fitting results of cumulative infilitration over time at different initial soil water contents
由表1可知,所拟合公式的相关系数均达到0.98以上,可靠性较高,能较好地说明累计入渗量随时间的关系。在非饱和土壤水分入渗中,土水势只需考虑基质势和重力势,且基质势是土壤含水率的函数[19]。入渗初期,灌水器周围的土壤含水率低于田间持水率,土壤水分主要受到土壤颗粒的吸力和颗粒之间所形成孔隙的毛细管力,二者之和远大于所受重力。故在入渗初期,累计入渗量随时间的变化是由基质势决定,即累计入渗量随时间的变化与土壤初始含水率有关。随着时间的增加,灌水器周围的土壤含水率高于田间持水率,但此时形成可自由流动的重力水仍是受基质势控制。因为整个土箱内的土壤初始含水率均低于田间持水率,随着时间的增加,在湿润锋干湿交界处的土壤水分仍是受到土壤颗粒的吸力和颗粒之间所形成孔隙的毛细管力的共同作用。故在入渗整个过程,累计入渗量随时间的变化规律一直由基质势决定,而基质势是土壤含水率的函数。基于此,提出一种以入渗时间和土壤初始含水率为自变量、微孔陶瓷渗灌的累计入渗量为因变量的预测模型:
I=f1(θ0) ln(t)-f2(θ0)
(1)
f1(θ0)、f2(θ0)由表1对应的系数得出:
(2)
(3)
综上所述,微孔陶瓷渗灌的累计入渗量预测模型为:
(4)
公式(4)是在灌水器长度为8 cm时拟合出来,故也可知单位长度下累计入渗量和土壤初始含水率与入渗时间的关系。在实践中,此模型可根据作物生长周期所需水量和土壤初始含水率,来确定在作物生长周期内灌水量是否能得到满足其生长需要。如若不能,可通过单位长度下累计入渗量与初始含水率和时间的关系推求灌水器长度,使其达到最优。
为检验模型的可靠性,配置土壤初始含水率为12%的土样,按相同的标准进行试验,选取8个时间点进行分析,将其实测值和模型拟合值进行对比分析,结果见表2。
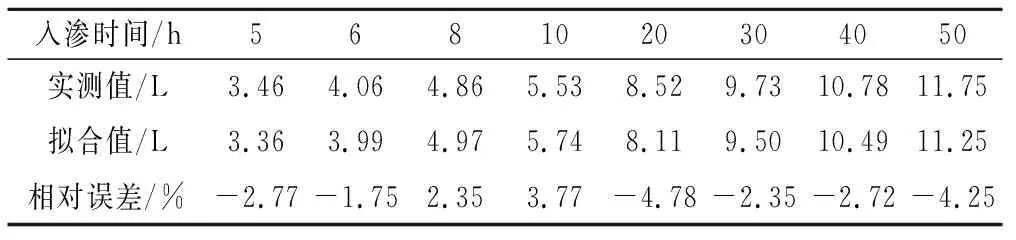
表2 累积入渗量实测值与模型拟合值Tab.2 Measured and model fitted values of cumulative infiltration
由表2可知,累积入渗量实测值和模型拟合值的相对误差均在±5%范围以内,说明该模型对无压条件下微孔陶瓷渗灌的累积入渗量预测精度较好。
2.2 土壤初始含水率对湿润锋运移距离的影响
图4为在不同初始含水率条件下,垂直向下湿润锋运移距离、水平方向湿润锋运移距离和垂直向上湿润锋运移距离随入渗时间的变化曲线。从图4可看出,在3个方向上都具有相同的规律:同一入渗时刻,土壤初始含水率越大,运移距离越大。这是由于土壤初始含水率越高,土壤的储水能力越小,土体不能够吸持更多的水分,从而更利于湿润峰的推进。同一土壤初始含水率下,不同方向上运移距离随时间也不相同。为了定量分析土壤初始含水率对湿润锋运移距离的影响,用幂函数进行拟合,结果见表3。
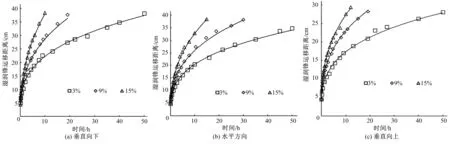
图4 不同初始含水率下湿润峰运移距离随时间变化曲线Fig.4 The curve of the migration distance of wetting peaks with time at different initial moisture content

表3 湿润峰运移距离随时间变化的拟合关系Tab.3 The relationship of the migration distance of wet front with time
从表3可发现,所拟合公式的相关系数均达到0.99以上,可靠性较高,能较好地说明运移距离随时间的关系。在同一方向上,不同初始含水率下运移距离的幂函数中的指数相差不大,可假设指数对其影响不大。取其平均值,建立垂直向下湿润锋运移距离随时间的方程:
x(t,θ0)=f3(θ0)t0.381 3
(5)
垂直向上湿润锋运移距离随时间的方程:
S(t,θ0)=f4(θ0)t0.304 1
(6)
水平方向湿润锋运移距离随时间的方程:
L(t,θ0)=f5(θ0)t0.442 3
(7)
将上面方程公式(5)~(7)结合图4的数据重新拟合可得表4。

表4 湿润峰运移距离随时间变化的拟合模型Tab.4 The model of the migration distance of wet front over time
表4的相关系数均达到0.97以上,说明对指数取平均值影响不大,故之前假设成立。因此能较好地说明湿润锋运移距离随时间的关系。由表4的数据可得出:
(8)
(9)
(10)
垂直向下运移距离方程:
(11)
垂直向上运移距离方程:
(12)
水平方向运移距离方程:
(13)
为检验模型的可靠性,在土壤初始含水率为12%条件下,按相同的标准进行试验,选取8个时间点进行分析,将其实测值和模型拟合值进行对比分析,结果见表5。

表5 湿润锋运移距离实测值与模型拟合值对比Tab.5 Comparison of measured values of wet front transport distance with model fitting values
由表5可知,水平方向湿润锋运移距离、垂直向下湿润锋运移距离和垂直向上湿润锋运移距离的实测值和模型拟合值相对偏差均在±6%围以内,说明用该模型对无压条件下微孔陶瓷灌水器入渗的各方向湿润锋运移距离进行预测精度较好。
3 结 语
(1)建立了以土壤初始含水率和入渗时间为自变量,累计入渗量为因变量的预测模型。并用土壤初始含水率为12%的试验数据对模型进行验证,结果表明模型具有较好的精度,可以预测不同初始含水率下微孔陶瓷渗灌的累积入渗量。此模型可根据作物生长周期所需水量和土壤初始含水率,来确定在作物生长周期内灌水量是否能满足其生长需要。如若不能,可通过单位长度下累计入渗量与初始含水率和时间的关系推求灌水器长度,使其达到最优。
(2)建立了不同初始含水率条件下湿润峰运移距离随时间变化的模型。并对模型进行了验证,结果表明 模型具有较好的精度,可以预测不同初始含水率条件下微孔陶瓷渗灌湿润锋运移距离随时间变化过程。

