多情景多视角探究生产消费中的利润最大化问题
杨文皓
(成都实验外国语学校西区2019届(1)班,四川 成都 610000)
一、引言
在生产生活中,盈利是其必然目的。而随着时代的发展与进步,生产、营销方式趋向多元化,新材料、新技术的产生使得盈利的方式发生了改变。这不禁引发笔者的思考:每一个生产过程和销售过程有何不同,根据这些区别与限制,又该分别建立哪种模型、采用哪种方式盈利呢?
本文将对几类常见的生活实际现象,立足高中数学知识,采取线性规划、函数模型的建立并求极值、探究利润最大化问题。
二、利润最大化的多视角分析
(一)视角1:利用线性规划探究利润最大化
在生产过程中,材料资源、人力资源、效率之间的有机结合十分重要,在大量的生产实例中,资源始终是有限的,如何在有限的时间内,以最少的人力,最低的材料成本,产生最大的利润,值得我们探讨。
实例:对材料进行初加工还是精加工,已成为当今生产的重点问题。某公司有材料a 300kg,有材料b 180kg,拟对材料a与材料b进行分配,已知1kg材料a,0.6kg材料b可生产1件粗加工产品,同时3kg材料a、2kg材料b可生产1件精加工产品。材料a每kg成本300元,材料b每kg成本100元,且生产一件粗加工产品需6天,1件产品人工费1天100元,产品售价2760元;生产一件精加工产品需10天,1件产品人工费1天200元,而产品售价高达7300元。限定在1200天内完成生产,则该采取怎样的分配策略才能使利润最大?
分析:简化问题,除去人工费与材料成本,计算利润。
粗加工产品1件获利:2760-6×100-1×300-0.6×100=1800元。
精加工产品1件获利:7300-10×200-3×300-2×100=4200元,粗加工虽人力、物力、材料消耗小,但全进行粗加工,利润比较小,不太可取;
精加工看似利润较高,若全进行精加工,人力、物力、材料消耗大,不太可取。
数据整理:为了体现科学性与直观性,现列出以下列联表

?
建立模型:设生产x件粗加工产品,y件精加工产品。
根据表格中的数据,可列出以下不等式:
甲材料消耗不超过300kg:x+3y≤300
乙材料消耗不超过180kg:0.6x+2y≤180
总生产时间不超过1200天:6x+10y≤1200
生产实际件数为整数:x∈N*,y∈N*
利润为目标函数:Z=1800x+4200y
不等式组表示的可行域如图所示:
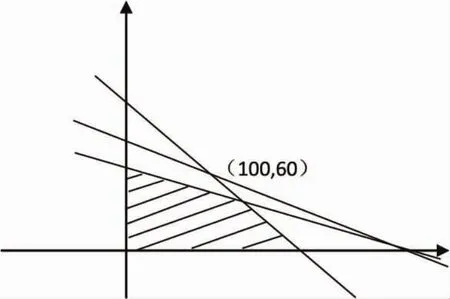
由图可得:当目标函数经过点(100,60)时,直线截距最大,目标函数取得最大值:
Zmax=1800×200+4200×120=432000(元)
(二)视角2:利用变量的关系建立函数探究利润最大化
在生产生活中,总会出现两个相关量变化趋势不同的情况,此时建立函数,统一变量之间的关系,利用函数求最值的办法即能找到利润最大值点。
实例:成都某旅行社旅游团以乘机形式出游,旅行社订飞机总成本12000元,飞机最多乘坐45人,旅行团中每人的飞机票有如下收费方式:若旅行社的人数多于30人,则,旅行社给每张机票减免20元作为优惠;若旅行社的人数在30人及以下,则每张机票按原价收费800元,则当机票的最大盈利为?
分析:设每张机票最终收费m元,旅行团的人数为x∈N,机票利润为y,
将函数分为两段讨论处理:
当 1≤x≤30 时,y=800x-12000,m=800
当 30<x≤45 时,y=(1400-20x)x-12000=-20x2+1400-12000,m=800-20(x-30)=1400-20x
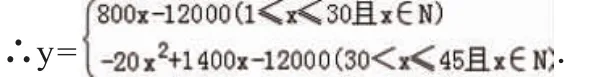
分段讨论函数的最值并取其最大值:
①函数在1≤x≤30单调递增,
当 x=30时,ymax=800×30-12000=12000元
②当30<x≤45时,令y′=-40x+1400>0
可得30<x<35,即函数在30<x<35单调递增,在35<x≤45单调递减
当x=35时,ymax=12500元
综上所述:当旅行社有35人时,旅行社可获得最大利润12500元。
(三)视角3:利用统计与概率进行预测与决策,使得利润最大化
当今消费形式大大改变,如何投消费者所好异常关键,精明的商家会根据以往的销售结果进行评估,找到发展趋势,并以此制定销售计划,在对变量的变化趋势不明确甚至一无所知时,可以利用整理数据,通过了解数据的大致变化,利用求数学期望的形式进行预测与决策,适当调整售价、进价等销售手段,实现利润最大化。
实例1:乐山名食甜皮鸭是一类卤制凉菜,夏天在笔者家乡颇受人们欢迎,一般的甜皮鸭成本15元,售价25元一斤,第二天有剩余则以12元的价格处理回总部(甜皮鸭保存时间短,长时间放置丧失口感)。乐山某甜皮鸭销售店打算从总部下订单,每天送等量甜皮鸭,根据店主的经验,销量(需求量)与当天的气温有关.如果气温不低于25℃,热天凉菜销量好,需求量为250只;如果最高气温位于在20℃到25℃范围内,需求量为150只;如果最高气温低于20℃,销量较差,需求量为50只.六月份的生产计划该怎样进行决策,才能使得利润最大?
分析:对于此类问题,不同的天气对于不同需求需求与进货量之间难以有机统一,变化不规则,可见生产生活是复杂的,不可片面研究,主观臆断。
为了保证数据的普遍性,统计了近三年六月份每天的气温,整合数据并作出如图频数分布表:

?
每天的销售情况可分为 x=250、150、50(只)
估计不同天气下的销售情况概率为:
气温不低于 25℃:P(x=250)=(36+20+4)/90=2/3
气温在[20,25):P(x=150)=20/90=2/9
气温低于 20℃:P(x=50)=(2+8)/90=1/9
则销量x的分布列为:

?
设进货量为m(斤),利润为W(元)
由于销量在50—250之间,故m范围只需为:50≤m≤250(只)
①当50≤x≤150时:
气温低于20℃,则可以原价25元售出50斤,其余以12元回收总部:
W=25×50+12(m-50)-15m=650-3m
气温高于20℃时无论是在[20,25)还是大于25℃均可卖完,则全以原价25元售出150斤:
W=25m-15m=10m
则总利润的数学期望为:EW=1/9×(650-3m)+(2/3+2/9)×10m=77/9m+650/9
②当150≤x≤250时:
气温低于20℃,则可以原价25元售出50斤,其余以12元回收总部:
W=25×50+12(m-50)-15m=650-3m
气温在[20,25)℃,则则可以原价25元售出150斤,其余以12元回收总部:
W=25×150+12(m-150)-15m =1950-3m
气温不低于25℃均可卖完,则可以原价25元售出250斤:
W=25m-15m=10m
则总利润的数学期望为:EW=1/9×(650-3m)+2/9×(1950-3m)+2/3×10m
=17/3m+4550/9
综上:当m=150只时,EW有最大值12200/9元
故应将150只作为进货决策。
三、视角评价
本文从三个生活中常见的例子出发,用不同的数学方法试图去解释其背后的数学原理,使得我们可以用严肃的观点去理解身边发生的事件,用理性的思维去理解事件背后的规律。对同一个问题,本文给出了一种典型的数学分析方法,并不是说仅仅只有这样的方法才可以去探究,从事件不同的角度去理解,就会有不同的方法来建立数学模型。本文的方法可以用来参考。
在视角1中,对于分配资源、投料等实际调度问题,且不可主观臆断,采取极端生产方式并不能达到利润最大化,而利用数学建模,采取线性规划,可以求出最优解所在位置,更加准确地进行参考。
线性规划具有较好的几何直观性,可以在条件约束的情况下,对目标方位进行图形化描述,根据几何意义和边界条件,进行直观的求解,并且能迅速的找出目标点。因此该方法是类似于条件极值的一种思维方法。
在视角2中,对于多变量的盈利问题,我们应找到量与量之间的变化与制约关系,进而借助函数武器求极值,找到利润最大值点,在实际问题中还要考虑函数模型的定义域,做到准确、有实际意义。
该方法将极值放在函数的观点之中,借助函数的灵活性,从具体上升到抽象去研究极值点的存在与否,用函数的研究方法去解决利润问题,利润最大化的问题实际上就是函数的极大值是否存在,在什么条件下存在的问题。
在视角3中,对于实际销售方案类决策问题,往往各个量的变化方向不明确,受外界影响较大,此时应该根据以往的数据进行分析与统筹,采取数学期望或利用样本的回归直线大致估计发展趋势,较为准确的判断利润最大值点的位置。
对决策类问题,由于条件之间的关系不如线性规划类清晰,因此需要根据已知的数据,提取关键信息,具体的方法包括利用概率论观点进行参数估计,或者对已知数据进行函数拟合,根据拟合出的函数进行推测,这样的方法在没有明确的数学规律的情况下,是比较有效的科学的分析方法。
四、总结与展望
利润最大化的方式远不止这几种,在发展的时代中,大数据统计、分析正走进我们生活,利用好所学的数学知识帮助我们实现利润最大化即彰显了数学之美,又与时代和生活息息相关。我们在数学学习过程中更应该注意与生活的联系,脱离题海,真正把数学代入社会,我们必将感受到数学的独特魅力。
下一步的工作,是综合利用不同的数学工具,对问题从不同的角度去分析,用多种方法不同角度分析的好处,是可以互相印证方法的科学性和评价结果的可信度。随着数学方法的发展,分析具体问题的途径也会越来越灵活。

