模块化多电平换流器的载波层叠脉宽调制策略分析与改进
白志红, 周玉虎
(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 台达电子企业管理(上海)有限公司杭州分公司, 浙江省杭州市 310051)
0 引言
模块化多电平换流器(modular multilevel converter,MMC)属于电压源型多电平变换器的一种,不仅具备多电平变换器的众多优点,如高度模块化结构、开关频率低、输出谐波含量低、功率等级扩展容易等,更重要的是它的直流侧可直接通过公共直流母线供电,不需要笨重昂贵的移相变压器,从而系统整体结构更加灵活简单,应用的电压/功率等级可随意扩展[1-2]。目前,MMC已得到国内外学术界的广泛关注,在高压直流输电、电机驱动、可再生能源(如风电)并网等领域有着较大的应用潜力[3-6]。
调制技术是MMC工作的基础,对MMC的输出电压谐波以及电容电压平衡控制都有直接的影响[6-7]。目前,已有文献中MMC的调制策略主要有最近电平逼近调制(nearest level modulation,NLM)[8-9]和基于多载波的脉宽调制技术[10],如载波移相脉宽调制(carrier phase-shifted pulse width modulation,CPS-PWM)[11]和载波层叠脉宽调制(carrier level-shifted pulse width modulation,CLS-PWM)[12]。最近电平逼近法利用阶梯波瞬时逼近正弦波,比较适合于高压直流输电系统等子模块数量较大的场合。而基于多载波的PWM技术对子模块数量没有特别要求,在子模块数较少的场合如中压驱动领域等比最近电平调制法更具有优势。由于采用载波移相调制时,各子模块工作模式和开关频率一致,功率均衡分配,因而目前文献中以应用该类调制为主[11,13-14]。另一方面,采用载波移相脉宽调制时,各子模块投入工作时间差异大,导致子模块电容电压出现严重不均衡,系统稳定性难以保证[10]。文献[15]在载波层叠调制的执行过程中采用状态机解码器来实现各子模块开关脉冲的均匀分布,在一定程度上缓解了子模块电容电压的不均衡现象,然而该方法随着子模块数的增加,其算法的复杂度和计算量也明显加大。
本文对应用在MMC中的载波层叠调制技术进行深入研究,首先分析了采用传统载波层叠调制技术时系统存在的本质问题,在此基础上提出了一种基于载波轮换的MMC多载波层叠调制策略,并通过仿真对该方法进行了验证。
1 MMC拓扑及工作原理
三相MMC的拓扑结构如图1所示,其中子模块可以采用多种结构形式,如单相半桥、全桥、各种三电平及多电平结构[16],本文分析均以采用半桥子模块为例。由图1可看出,每个相单元包括上、下两个桥臂,每个桥臂由N个子模块(submodule,SM)和一个电抗器串联组成。电抗器起到滤波和抑制环流的作用。在理想情况下,所有子模块的电气参数和所有桥臂电抗值都保持一致,即具有对称性。由图1(b)可知,每个子模块可以有两种输出情况:电容电压Ucap和0。当子模块开关T1开通(T2关断)时,子模块输出为电容电压Ucap,此时如果桥臂电流iup>0,则电容处于充电模式;如果桥臂电流iup<0,则电容处于放电模式。当子模块开关T1关断(T2开通)时,子模块输出为0,电容被旁路,电容电压保持不变。就每相单元而言,任一时刻所有投入的子模块电容电压之和等于换流器直流侧总电压Udc。

图1 三相MMC拓扑结构Fig.1 Topology of three-phase MMC
根据图1(b),每个子模块的输出电压可以表示为:
(1)
式中:Sj,p,i和Sj,n,i分别为j相上、下桥臂第i个子模块的开关函数,其中,j∈{a,b,c},i∈{1,2,…,N}。
因此,j相上、下桥臂电压可以表示为:
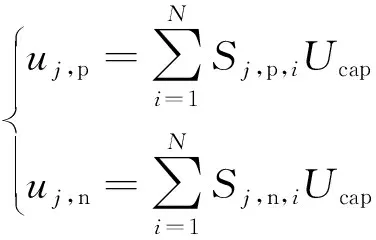
(2)
根据图1(a),利用基尔霍夫电压定律,可以得到:
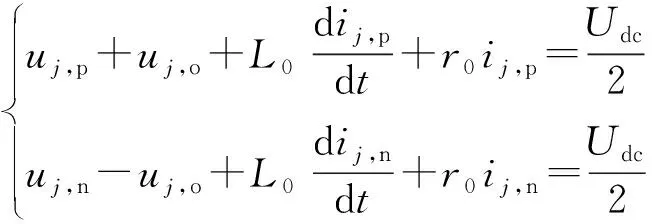
(3)
式中:uj,o为MMC的j相输出电压;r0为L0的寄生电阻;ij,p和ij,n分别为j相上、下桥臂电流。
为简化分析,认为三相星形负载中点与直流侧中点同电位。把式(2)代入式(3),可以得到MMC的j相输出电压表达式为:
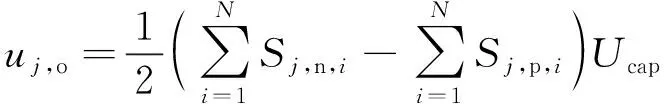
(4)
式(4)表明,如果MMC的子模块电容电压达到均衡,其输出电压仅取决于每个桥臂所有子模块的开关函数的代数和。
2 基于载波轮换的MMC多载波层叠调制技术
2.1 传统载波层叠PWM调制技术
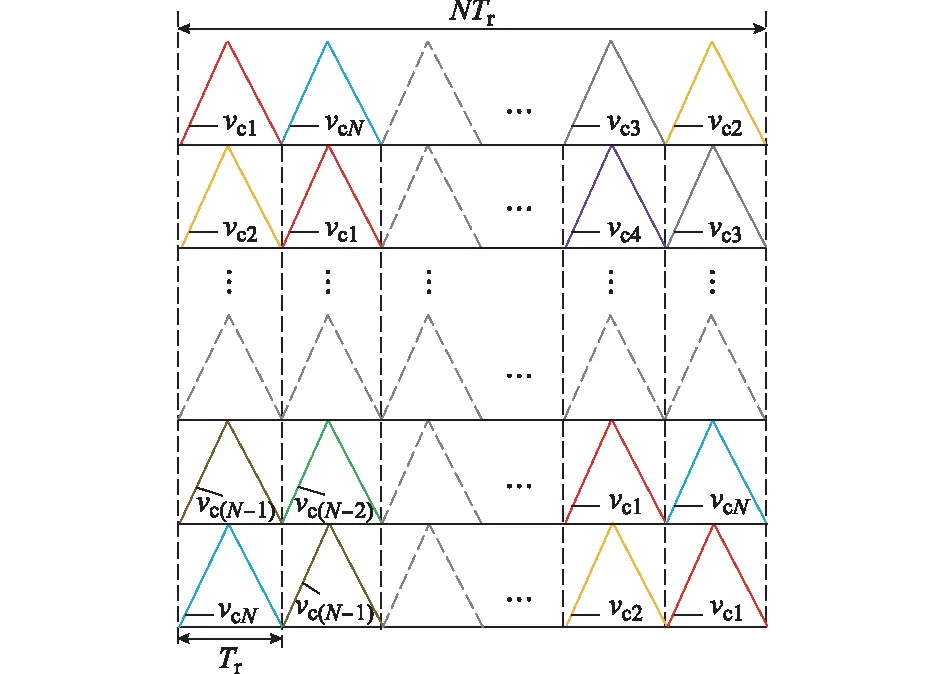
根据各列载波相位分布情况,载波层叠PWM有3种基本实现方式[10]:同相层叠(phase disposition,PD)方式、交替反相层叠(alternative phase opposition disposition,APOD)方式和正负反相层叠(phase opposition disposition,POD)方式。由于PD方式比其他两种方式具有更好的输出谐波特性[17],本文分析中均采用该方式。以每个桥臂子模块数N=4为例,图2给出了PD方式的具体实现过程。其中,4路同频同相的载波vc1至vc4与子模块SM1至 SM4相对应。各子模块开关函数由调制信号ur与相应的载波比较产生。以第一个子模块为例,当调制信号ur>vc1时,开关函数为1,此时开关管T1开通,T2关断;当调制信号ur 图2 传统载波层叠脉宽调制技术的实现原理Fig.2 Implementation principle of traditional CLS-PWM 根据图2中得到的各子模块开关函数可以看出,各子模块投入时间差异较大。由于子模块投入时间直接决定电容的充放电情况,因此采用这种调制方式时各子模块电容电压容易出现严重不均衡进而影响输出电压的波形质量。此外,各子模块开关管开关频率的差异也将导致各子模块损耗和发热不同,影响系统可靠性。 载波轮换(carrier-rotation)策略的思想最先在文献[18]中被提出,用于解决在飞跨电容型多电平变换器中电容电压的不均衡问题。虽然MMC的拓扑结构与飞跨电容型多电平变换器差异较大,但采用传统载波层叠调制策略时也存在类似的问题。对MMC而言,最终被关注的是总的交流侧输出电压和电流。也就是说,采用载波层叠调制时,在任一时刻各子模块相对独立,只要所有子模块输出的叠加结果满足总输出要求,具体是哪个子模块投入工作并不是要关注的。因此,本文提出将载波轮换策略应用于MMC的调制中,以期实现各子模块投入时间及开关频率的合理分配。图3给出了具体实现原理:以某一时间Tr为周期让所有载波vc1至vcN在各个子模块间轮换,则在NTr(N为桥臂模块数)时间段内,每个子模块分别被每列载波控制Tr时间。图3中给出的载波轮换周期Tr=Tc,其中Tc为载波周期。由图可知,在NTr时间段内,每个子模块的载波以Tr为轮换周期,一共轮换N次,保证在NTr时间段内,每个子模块被所有载波vc1至vcN分别控制Tr时间,从而所有子模块的平均开关频率以及平均投入时间有望达到一致,避免电容电压不均衡现象。 图3 MMC多载波轮换层叠调制技术的实现原理Fig.3 Implementation principle of carrier-rotation based CLS-PWM for MMC 这里以子模块数N=4为例,分析载波轮换后对MMC输出电压的影响。为对比方便,图4中分别给出了采用传统方法和采用载波轮换后一个桥臂上4个子模块开关占空比产生过程。 图4 采用载波轮换前后子模块开关占空比分析Fig.4 Analysis of duty cycle for SMs with or without carrier-rotation 根据图4(a)可以得到采用传统载波层叠调制策略时,各子模块开关管开关占空比表达式为: (5) 根据图4(b)得到采用载波轮换层叠调制策略后,各子模块开关管开关占空比表达式为: (6) 根据式(5)和式(6)可以得到采用载波轮换前后,各子模块开关状态总占空比均为: (7) 此外,从图4(a)中各子模块的开关函数可以看出,采用载波轮换前,开关过程主要集中在第一个子模块,而其他子模块开关过程较少或一直保持投入状态,此时的开关损耗主要集中在第一个子模块;采用载波轮换后,原来发生在第一个子模块的开关过程被平均分配给了其他子模块,如图4(b)所示,开关过程所产生的开关损耗也由各子模块平均承担。 为验证上述方法的有效性,在MATLAB/Simulink中搭建了一套MMC仿真系统,系统参数为:直流侧总电压Udc=400 V,电容电压Ucap=100 V,子模块电容容值C=4 500 μF,载波频率fc=2.1 kHz,幅度调制比为1,基波频率为50 Hz,桥臂电感Ls=2 mH,负载为阻感性,其中Rload=5 Ω,Lload=10 mH。 以PD-PWM方法为例,图5给出了每个桥臂有4个子模块(N=4)的MMC的部分仿真波形。调制波与各路载波比较得到相应子模块上管的驱动信号,如图5(a)所示。可以看出,各子模块开关信号的脉冲个数和宽度差异较大。而且,这种差异将直接导致各子模块电容电压出现严重不均衡(如图5(b)所示),与此同时,输出电压波形也不规则(如图5(c)所示),谐波含量大(如图5(d)所示),最终系统不能稳定运行。 图5 MMC采用传统载波层叠调制时的仿真结果Fig.5 Simulated waveforms of MMC with traditional CLS-PWM 图6(a)是a相上桥臂子模块上管的驱动波形。可以看出,与图5(a)采用传统载波层叠调制相比,采用本文所提出的载波轮换层叠调制后,各子模块的投入时间和开关管的开关频率基本相同,长期运行下各子模块开关管发热和损耗有望实现一致。图6(b)给出了a相上、下桥臂各子模块电容电压波形,可以看出,各子模块电容电压基本实现了平衡,且纹波控制在10%以内。图6(c)和(d)分别是MMC交流侧输出电压波形及其频谱分析结果,可以看出输出电压是接近完美的9电平波形,其主导谐波群出现在4.2 kHz附近,且主导谐波的最大幅值都在基波幅值的5%以内,总谐波畸变率(THD)为10.94%。值得注意的是,为验证所提方法的效果,本文仿真中并未对子模块电容电压给予单独控制,因而仿真结果略偏保守。另外,采用更多子模块或提高开关频率可以进一步减小输出电压的THD。 图6 MMC采用载波轮换PD-PWM调制时的仿真结果Fig.6 Simulated waveforms of MMC with carrier-rotation based PD-PWM 本文提出了基于载波轮换的MMC多载波层叠PWM调制策略,该策略从本质上解决了传统载波层叠PWM调制技术在MMC中应用时存在的问题。采用所提出的方法,MMC各子模块投入时间和开关管开关频率基本达到一致,解决了采用传统载波层叠PWM调制时开关管损耗和发热不一致问题;由于各子模块投入工作时间达到一致,即使不对子模块电容电压单独控制,电容电压仍可实现均衡,从而输出电压波形质量得到提高,THD大大降低。考虑到采用闭环控制可以提高换流器运行性能,今后将在多载波轮换层叠调制策略的基础上,进一步研究MMC的闭环运行控制策略。
2.2 多载波轮换层叠调制技术
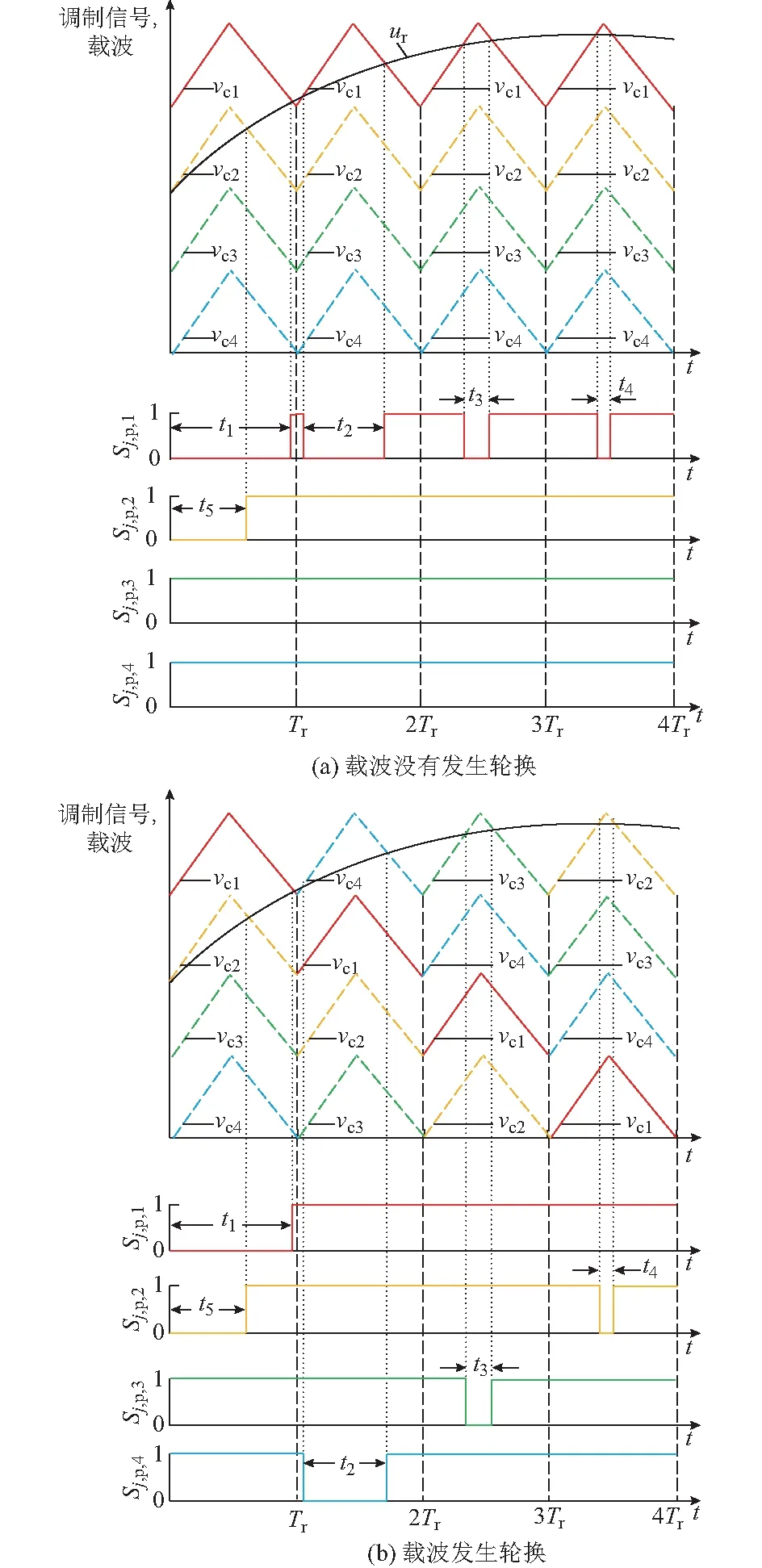
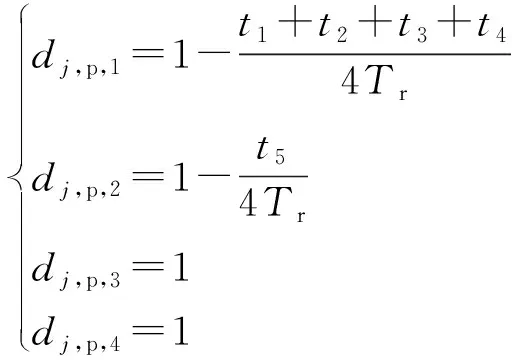

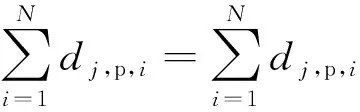

3 仿真验证

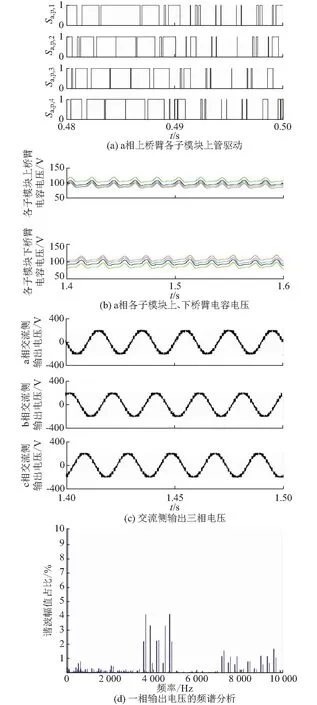
4 结语

