线性三嵌段共聚物格点薄膜受限下的自组装

2018-11-26 05:38张乾吴骥余胜东王向红

浙江大学学报（理学版） 2018年6期

张乾,吴骥,余胜东,王向红*

(1. 温州大学数理与电子信息工程学院, 浙江温州 325035； 2. 温州职业技术学院, 浙江温州 325035)

不同环境受限下的嵌段共聚物能自组装成形态丰富的纳米结构，在纳米光刻、药物运输、高密度磁数据存储介质等新兴领域，因具有潜在的应用价值而广受关注[1-3]. 在过去的20年中，已有大量研究聚焦于嵌段共聚物自组装理论，通过调整聚合物嵌段比例和链段间的相互作用强度，在模拟中发现了众多A、B二嵌段共聚物的有序周期性结构，如层状、柱状、体心立方以及复杂的双连续相结构[4-5]等，并在实验中得到了验证. 同时，A、B、C三嵌段共聚物本体下的结构和相图也得到了深入研究[6-7]. 为了赋予材料更多特殊的实用性能，研究者着手寻找聚合物的新颖结构.

聚合物的有序结构不仅与聚合物的参数有关，还与聚合物所处的外部环境，如空间几何受限、外加电场、剪切场[8-12]等有关. 高分子在受限条件下，体系熵和能量在空间几何体的约束和表面相互作用下重新达到平衡.因此，可通过调整几何特征获得新的微结构. A、B线性二嵌段共聚物是一种最简单的结构，对空间受限下A、B二嵌段共聚物的相行为研究已很多，如文献[13]从理论和实验角度分析了热力学边界条件下不同于本体情况的相行为. A、B、C三嵌段共聚物有较大的参数空间和更丰富的分子构型，因此，研究其不同受限几何结构中的自组装过程非常有意义. 大量实验和模拟均发现了其与众不同的特殊有序构象. 在嵌段共聚物多相共混体系中，MATSUSHITA[14]观察到了崭新的具有双周期分层结构的介观瓷砖结构，对新型功能材料的研究有借鉴意义.

为了探究在表面场诱导模型下A、B、C三嵌段共聚物自组装的过程，余勇等[27]采用实空间自洽场理论研究了A、B、C对称线性三嵌段共聚物薄膜的自组装结构及其转变规律，选取具有特定聚合物参数的对称线性三嵌段共聚物，置于无修饰条纹和有修饰条纹两类薄膜受限表面下，通过调节薄膜表面场强度和薄膜厚度，获得了一系列新颖的聚合物薄膜微结构. 本文进一步研究更复杂的格点表面诱导模型，对A、B、C线性三嵌段共聚物在格点型薄膜受限下的自组装结构及形成机制进行分析，研究构建A、B、C线性三嵌段共聚物的相结构图及不同吸附强度下结构的转变规律.

1 模型和方法

利用自洽场理论研究A、B、C线性三嵌段共聚物在格点型薄膜受限下的自组装结构及其相变规律. 自洽场方法将共聚物各个链段间比较复杂的相互作用看作链与平均场之间的相互作用，根据最小自由能原理，通过数值解的方法求得高分子在热力学平衡状态时的空间密度分布. 在模拟体系中，将n条A、B、C三嵌段高分子链置于一个体积为V的空间中，空间上下固定不同化学性质的平行薄膜，如图1所示. 为简化模型，假定A链段和B链段的kuhn长度相等，均为a. 每条高分子链的聚合度为N，三嵌段满足fA+fB+fC=1，fi代表嵌段i的体积分数，此时每条链段上嵌段单体的数目为fiN. 这里引入KHANNA等[28]提出的屏蔽技术实现薄膜受限，该技术的核心是利用界面密度函数φW(r)修正不可压缩性条件，即

φA(r)+φB(r)+φC(r)+φW(r)=1,

(1)

其中，φi(r)表示嵌段i的归一化密度，i∈(A,B,C)，φW(r)满足0≤φW(r)≤1. 界面密度函数φW(r)为：

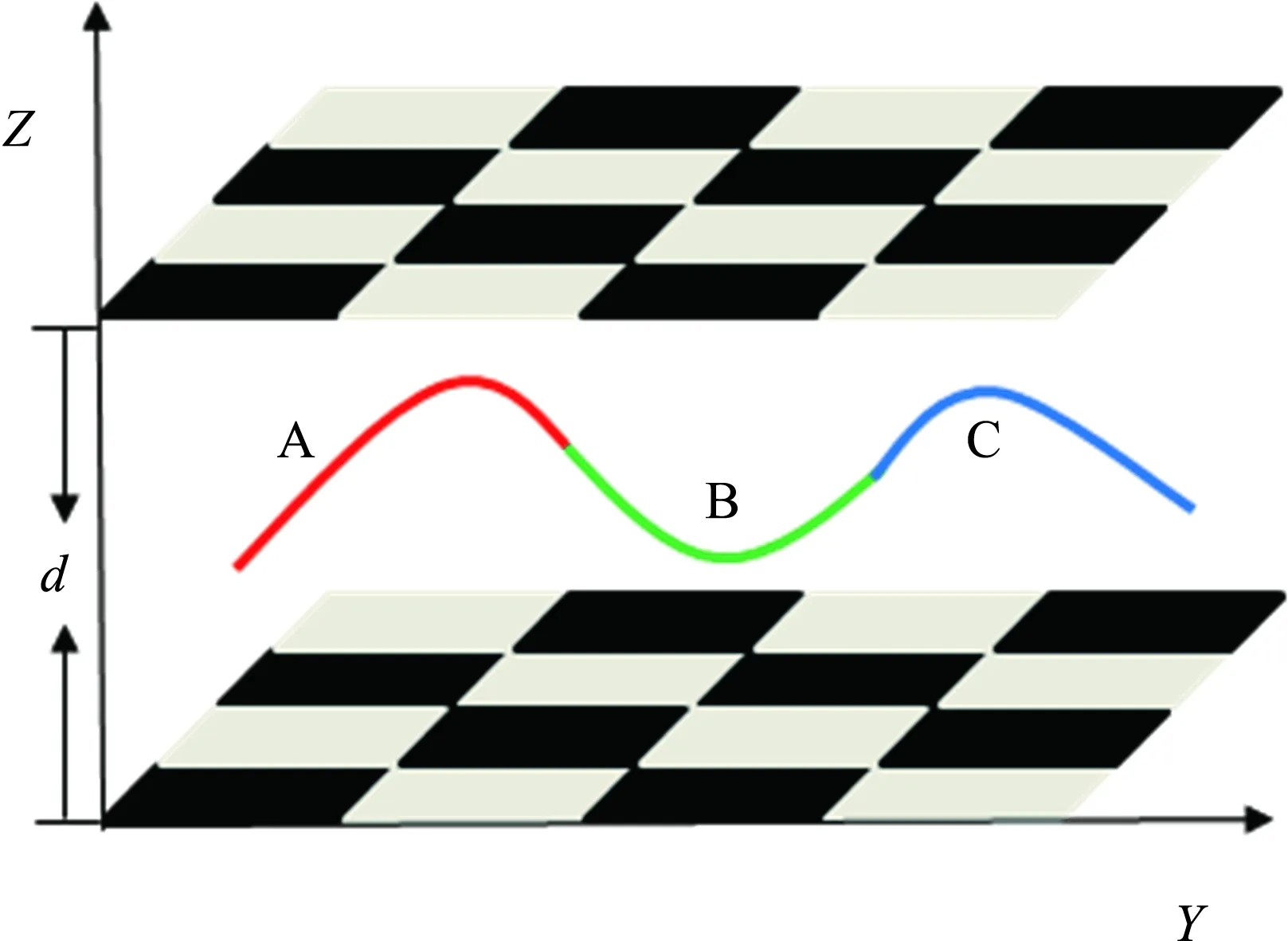
图1 本文模型Fig.1 The illustration of the model established in this paper线性三嵌段共聚物在分成16个格点型的薄膜空间中.其中,白色区域A、C表示吸附,B表示排斥，黑色区域相反.The triblock copolymer in the films with selectivity surfaces, which is divided into 16 equivalent regions. A, C represent attractive and B represents repellant in the white regions, while the black regions are reversed.

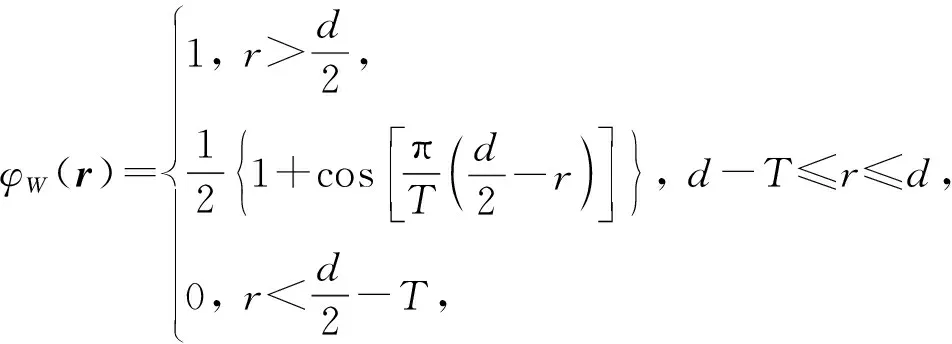
(2)

其中，T表示薄膜厚度，d表示垂直于薄膜方向的受限空间尺度，即图 1中Z轴方向上两板所囊括的长度，r表示模拟空间中沿Z轴方向至d/2处的距离. 在上述分段函数中，界面密度函数φW(r)=0表示完全由聚合物填充的区域，φW(r)=1表示受限薄膜不可穿透的坚实外壁，0<φW(r)<1表示聚合物分子与薄膜内壁互有重叠的区域.

由实空间自洽场理论，结合聚合物与受限薄膜之间的相互作用势，得到本研究体系中的单链自由能：

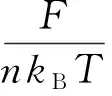
唐飞霄一愣，他有些不敢相信自己的耳朵。短暂的迟疑后，他咬紧牙关，挣扎着从地上爬起，捡起一条树枝作为拐杖，踉跄着朝山下走去。

χBCNφB(r)φC(r)+χACNφA(r)φC(r))+

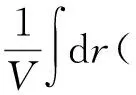
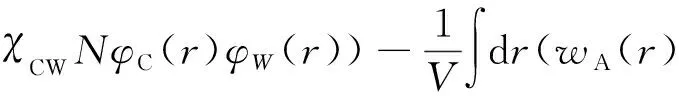
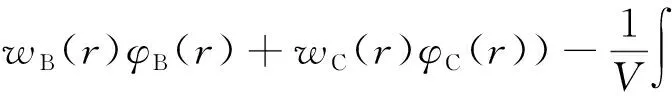
φA(r)-φB(r)-φC(r)-φW(r))，

(3)

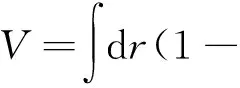
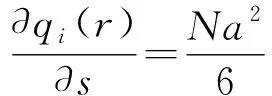
(4)

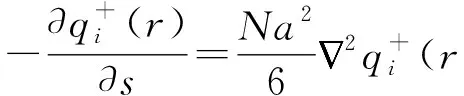
(5)

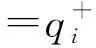
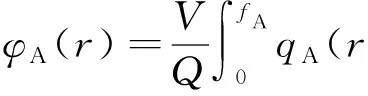
(6)

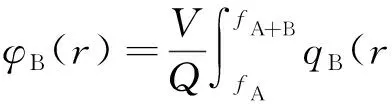
(7)

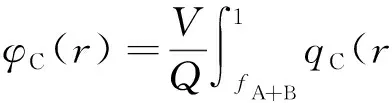
(8)

由鞍点近似，以密度场为变量对自由能取极小值，由∂F/∂φi=0，得到平均场方程：

wA(r)=χABNφB(r)+χACNφC(r)+
χAWNφW(r)+ξ(r)，

(9)

wB(r)=χABNφA(r)+χBCNφC(r)+
χBWNφW(r)+ξ(r)，

(10)

wC(r)=χACNφA(r)+χBCNφB(r)+
χCWNφW(r)+ξ(r).

(11)

式(3)～(11)构成了一组自洽场方程组，假设整个过程是一个弛豫过程，利用DROLET等[30]提出的组合筛选法计算自洽场方程组. 首先给定初始平均场，然后根据设定好的迭代步长进行重复计算. 平均场wi实际上是一个持续更新的有效化学势场，更新过程满足以下线性关系：

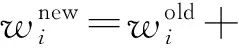
(12)

在本文的模拟体系中，Δt=0.1，反复迭代后计算前后2次自由能的差值ΔF/nkBT，当达到理想的精确度，即ΔF/nkBT<10-6时，认为体系达到了平衡.

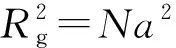
2 结果与讨论

对于A、B、C线性三嵌段共聚物，微结构由5个独立变量fi,χijN,χiW,d,T决定. 很难在一个相图中表示三嵌段共聚物所有可能的稳定结构，但可通过分析微结构对3个嵌段之间嵌段比的依赖性，选定相互作用大小，绘制受嵌段比影响的三角相图. 本文对施加吸附力后的自组装情况进行了模拟，分弱吸附作用力和强吸附作用力2种情况进行讨论，受限表面对A、B、C 3个嵌段分别施加χBW=-0.050，χAW=χCW=-χBW的作用强度，得到弱吸附下的三角相图，然后对弱吸附下三色层状到双色柱状的相变过程进行验证. 最后,将作用力加强至χBW=-0.100，发现得到的三角形图与前两种大相径庭，各相同点位上的相结构差异很大.

2.1 弱吸附作用下的三角相图

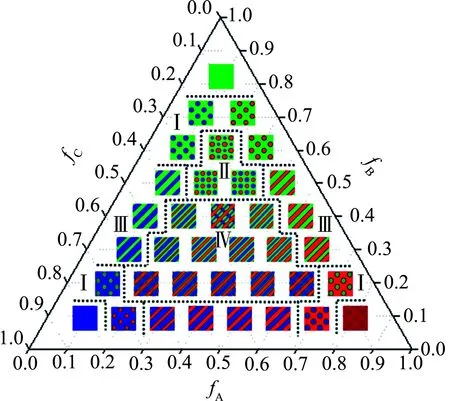
图2 嵌段间相互作用为χABN=χBCN=χACN=30的线性三嵌段共聚物在χBW=-0.050的弱吸附力作用下的三角相图Fig.2 Triangular phase diagram of linear triblock copolymers with χABN=χBCN=χACN=30 confined by thick films with weak adsorption χBW=-0.050红色、绿色和蓝色部分分别代表A、B和C嵌段(下同).Red, green and blue represent A, B and C blocks, respectively (the same below).

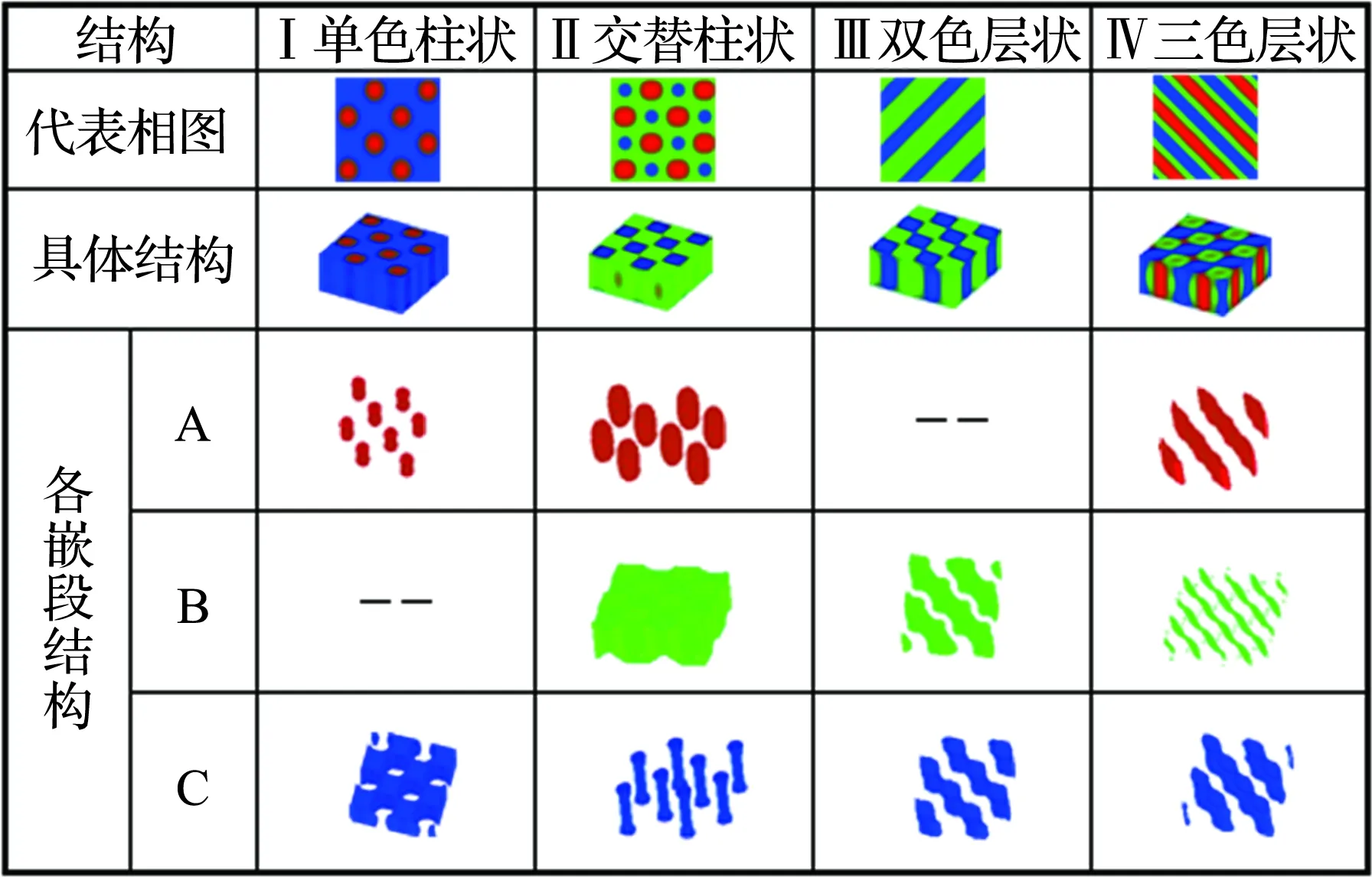
图3 线性三嵌段共聚物在弱吸附力作用下的典型结构Fig.3 Typical structure of linear triblock copolymer confined by thick films with weak adsorption

图2为弱吸附作用下的三角相图，观察到在表面吸附力作用下，各嵌段均出现拉伸或压缩现象，导致在聚合物表面呈格点化表层. 图3列出了弱吸附下的三角相图所包含的所有稳定结构类型. 这些结构由模拟空间通过缩放获得，可以看到其表面大致按吸附图案的样式排列，但内部结构可能有所不同. 为了更清楚地观察共聚物的内部结构，将模拟盒子在LZ/2处截断，并将观察到的实际相结构陈列在图 3代表相图的一栏中. 首先，观察图 3中的微结构，在无序状态(fA∶fB∶fC=0.1∶0.1∶0.8)的基础上，随着体积分数的增加A嵌段形成柱状结构，如增至fA∶fB∶fC=0.2∶0.1∶0.7(相图呈左右对称，仅讨论相图左侧的相结构与相变). B嵌段占比小而未呈现明显结构，其余空间被C嵌段填充，如图 3所示的Ⅰ单色柱状. 此结构类似于格点分布，格点型吸附下的自组装结构与无吸附受限结构未发生太大变化，依然保持柱状结构，仅A嵌段成柱的位置因存在吸附势而有差异. 当A嵌段比例继续增大(fA∶fB∶fC=0.3∶0.1∶0.6)时，相图中出现层状相. 当fB=0.2，fA≫fC或fA≪fC时，聚合物呈单色柱状相，B嵌段聚集成柱结构. 当A和C的嵌段比稍趋于均衡时，相结构即转变为三色层状.

从整幅相图来看，三色层状和双色层状的稳定区域占据最广. 当fB足够大时，A和C嵌段占比大致相当(即图 2中的Ⅱ区域)，聚合物的稳定结构仍为交替柱状. 但此时，在棋盘图案吸附下，A嵌段形成的柱被压缩而居于内部，C嵌段形成的柱被拉伸成细长型，因而在外部观察不到A嵌段，如图3中Ⅱ所示的交替柱状结构展示. 当3个嵌段的体积大致相当时，如相图中的fA∶fB∶fC=0.3∶0.4∶0.3，聚合物形成特殊的三色层状，受格点型吸附的影响，呈现波浪形层状.

与TANG等[7]和JIANG等[31]本体条件下的研究相比，弱吸附作用下的相结构有明显差异，即格点型薄膜使得自组装形成的结构在X-Y平面更易形成格点化结构，而在Z方向上的结构有一定程度的变形，如交替柱状中A、C分别被压缩和拉伸. 对于fB较小，fA、fC相当的三嵌段共聚物，其与二嵌段共聚物的自组装结构类似[32]. 例如，fA∶fB∶fC=0.4∶0.1∶0.5的三嵌段共聚物与两组分相当的二嵌段共聚物形成的结构都以层状为主.

在对聚合物施加了格点型吸附作用后，观察了各嵌段在板间的密度分布. 结合弱吸附相图和交替柱状共聚物(fA∶fB∶fC=0.2∶0.6∶0.2)在薄膜上的密度分布，嵌段共聚物被限制在作用区域，各嵌段主要在被吸附的区域，如图4所示. 在排斥B、吸引A、C的区域(Ly=8～16)， C形成柱状；在吸引B、排斥A、C的区域(Ly=16～32)，A形成柱状，即在相邻的相反作用力区域，线性共聚物的两端形成柱状，B将A、C隔开. 此结构中不同嵌段的柱状结构交替出现在相邻区域，是格点图案受限的理想结构. 图 5为弱吸附作用下，fA=0.2，fB从0.40增大到0.50时，三色层状和交替柱状结构的自由能. 由图5可得相变发生的大致位置为fB=0.456，B嵌段体积的增加，占据了原本A嵌段的空间，对两端的嵌段产生挤压，打破稳定的薄层，迫使其弯曲，使A、C形成相互交替的柱.

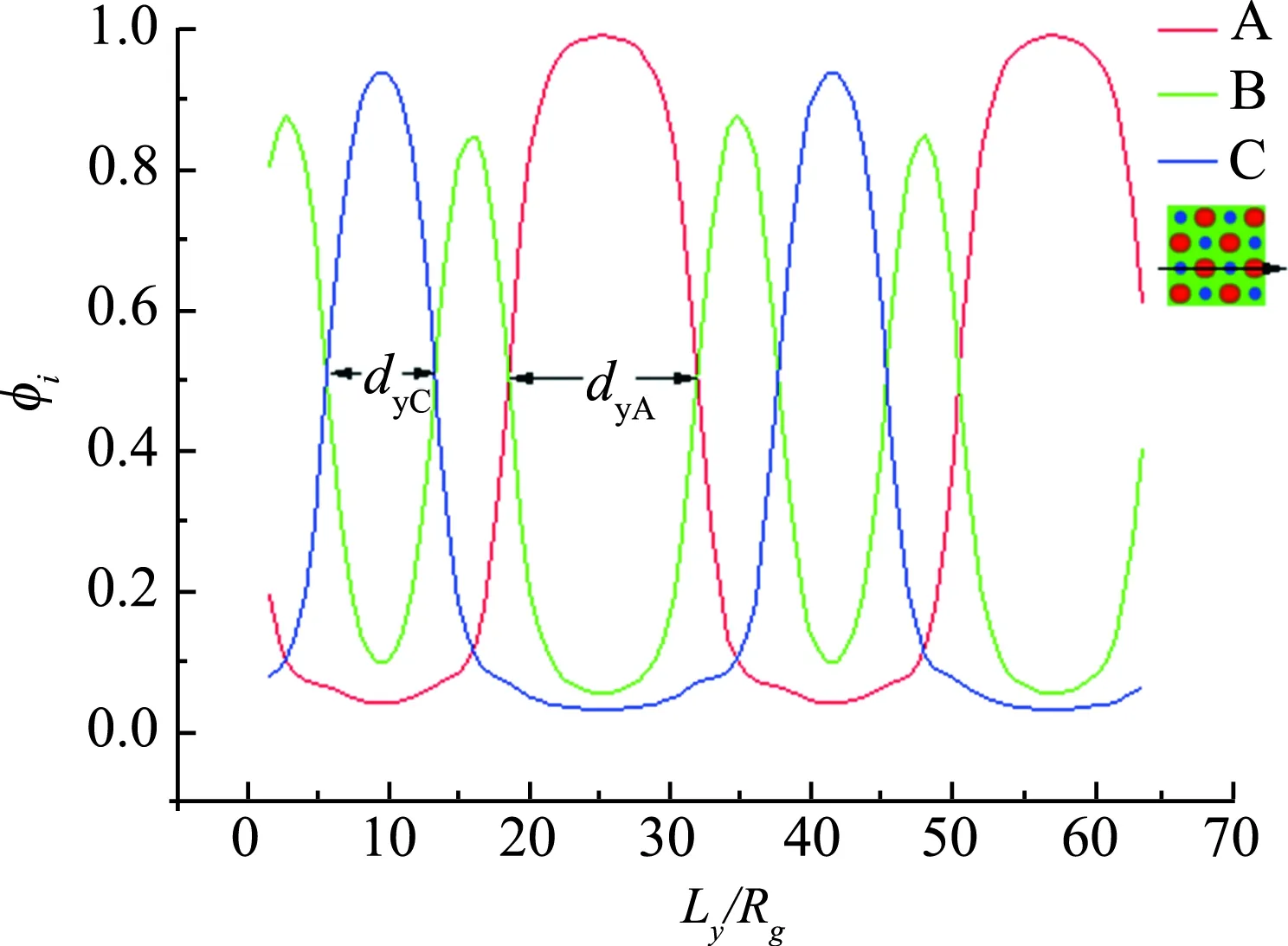
图4 嵌段比为fA∶fB∶fC=0.2∶0.6∶0.2时共聚物沿Ly的密度分布Fig.4 The segment densities for alternately cylinder structure with fA∶fB∶fC=0.2∶0.6∶0.2 along Ly φi(i=A,B,C)代表各嵌段密度.φi(i=A,B,C)represents the density of each block.

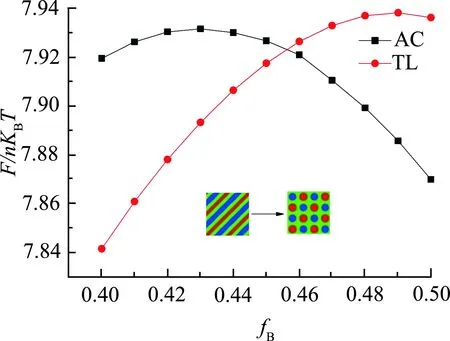
图5 fA=0.2, fB=0.4～0.5时三色层状与交替柱状的相变过程Fig.5 Phase transition between tricolor lamellae (TL) and alternately cylinder (AC) with fA=0.2, fB from 0.4 to 0.5

2.2 强吸附作用下的三角相图

图6为强吸附作用下的三角相图，图7为典型相结构. 尽管作用力有加强，但因嵌段比差距依旧悬殊，无序结构的状态保持不变. 除相图中部位置外，三色层状的位点被编织层状取代. 新增加的编织层状结构主要由弱吸附作用下的三色层状结构转变而来. 棋盘型的作用区域使原本处于层状结构的中间嵌段在吸附和排斥力的牵扯下，部分位置发生弯曲和分离，使中间嵌段形成铁链状结构，截断了当中较薄的层，并将其包裹在中心位置. 图8(b)为编织层状结构3种嵌段的清晰构象，图8(a)为各嵌段的密度分布. 在JIANG等[31]的实验中，编织层状形成的原因是原本形成层状结构的A(或C)中某一链条变短，使得A(或C)嵌段不足以维持层状结构，为了避免A和C嵌段连接，将A和C的一端嵌入B层中.

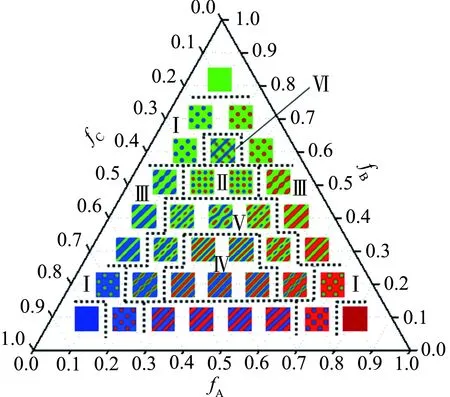
图6 嵌段间相互作用为χABN=χBCN=χACN=30的线性三嵌段共聚物在χBW=-0.100强吸附力作用下的三角相图Fig.6 Triangular phase diagram of linear triblock copolymers with χABN=χBCN=χACN=30 confined by thick films with strong adsorption χBW=-0.100

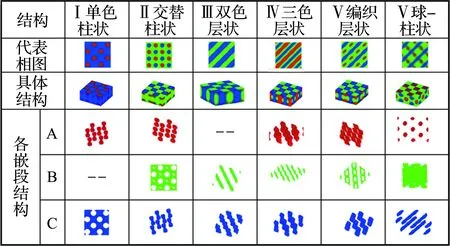
图7 线性三嵌段共聚物在强吸附力作用下的典型结构Fig.7 Typical structure of linear triblock copolymer confined by thick films with strong adsorption

强吸附力作用和弱吸附力作用的主要区别在于吸附力成为影响自组装的重要因素. 相结构在Z方向的变形成为主要变化的方向.

此外，图 7中Ⅰ单色柱状(如fA∶fB∶fC=0.2∶0.1∶0.7)的明显变化是A嵌段柱在强吸附力作用下形变为哑铃状，而C嵌段收缩为明显的穿孔层状. 类似的还有图7中的Ⅱ交替柱状(如fA∶fB∶fC=0.2∶0.5∶0.3)，C、A嵌段分别受上下表面的吸引和排斥，形成长短2种哑铃状，并在相邻区域交替出现，B嵌段形成多孔层状. 还发现在图6fA∶fB∶fC=0.2∶0.6∶0.2位置出现了一种“球-柱”新结构. 该结构最显著的特征就是A嵌段呈现球状，C嵌段呈现水平朝向的柱状. 对该结构的端点密度分布进行研究，如图9所示. 在一个结构单元内，分别画出A嵌段的端点，s=0，AB连接点，s=fA，BC连接点，s=fA+B处，和C嵌段的端点密度分布，s=1. 并用红、蓝、黑分别代表A、C和嵌段连接点. 图 9(a)和(d)表明，A嵌段的端点分布在球形区域内，C嵌段的端点分布在柱状区域内. 图9(b)和(c)表明，A、B嵌段连接点形成的球形隔开了A、B，而B、C嵌段连接点形成的柱状隔开了B、C. 在空间中，只有当各个方向受力均匀时，混乱无序的聚合物链才会汇聚成球形，而在本文设定的吸附强度下，A嵌段受到上下薄膜的排斥力与周围嵌段对其作用力刚好达到平衡.

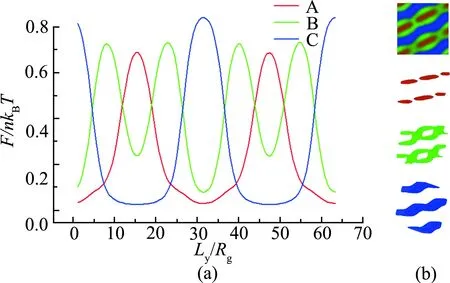
图8 (a) 嵌段比为fA∶fB∶fC=0.2∶0.6∶0.2时的编织层状结构沿Ly的密度分布 (b) 编织层状结构Fig.8 (a) The segment densities for knitting pattern structure with fA∶fB ∶fC=0.2∶0.6∶0.2 along Ly (b) Knitting pattern structureφi(i=A,B,C)为各嵌段密度.φi(i=A,B,C) represents the density of each block.

图9 各端点的密度分布Fig.9 Density plots for the terminals

3 结论