乌药化学成分结构参数与色谱保留时间的关系

堵锡华，王超

(徐州工程学院 化学化工学院， 江苏 徐州 221018)

乌药为樟科山胡椒属植物常绿灌木乌药的干燥根，湖南、浙江、江苏、江西等我国长江以南地区均有分布，为常用的理气镇痛药，具有行气止痛、温肾散寒之功效[1]，亦有抗炎、抗氧化及抑菌等生物活性[2-3]，常用来医治由跌打损伤、腹部疼痛、寒疝及脉管炎、心脏病引起的心胸疼痛等症[4]. 目前，国内外对乌药的化学成分分析及工艺提取、抗氧化特性、抗病毒及抗肿瘤活性等方面有较为深入的研究[5-8]，其中，对化学成分分析的相关研究较为常见[9-11]，对化学成分性质的研究则较少.

保留时间是气相色谱(GC)定性分析的重要指标，化合物分子的保留时间等相关定性数据数量庞大无法通过实验一一获取，因此将宏观的保留值与分子的微观结构联系起来，是气相色谱保留值定性和智能高效化的重要理论依据[12]. 本文将定量结构-保留相关性研究方法与在化学[13-14]、药物化学[15]、环境科学[16]等领域得到广泛应用的人工神经网络(artificial neural networks，ANN)方法相结合，针对文献[17]得到的湖南产乌药68种化学成分的色谱保留时间，建立其与分子连接性指数、电性拓扑状态指数的BP神经网络模型. 本文通过分析乌药化学成分的分子结构，用获得的相关结构指数预测色谱保留时间的数据，预测的保留时间与实验值的相对平均误差为2.66%. 研究为通过气相色谱法快速高效检测乌药复杂的化学成分提供了理论依据.

1 研究方法

1.1 保留时间数据来源

湖南产乌药68种化学成分的色谱保留时间数据来自文献[17]，详见表1.

1.2 指数计算

利用Chemoffice绘图软件绘制乌药68种化学成分的分子结构图，在Matlab软件中调用该分子结构，依照文献[18-19]的方法自编程序，计算68个分子的分子连接性指数和电性拓扑状态指数，剔除二类指数中大部分数据为0的数组，对余下的数组用Minitab软件中最佳变量子集回归法进行筛选，将连接性指数(0X，5X和5Xc)和电性拓扑状态指数(E1，E2和E3)相结合，寻找与乌药化学成分色谱保留时间相关性最强的结构参数.各指数值见表1.

表1 乌药化学成分的结构参数及色谱保留时间

续表1

续表1

2 模型的建构

2.1 相关性分析和稳定性检验

将Minitab软件最佳变量子集回归筛选的6种连接性指数和电性拓扑状态指数与乌药化学成分的色谱保留时间进行回归分析，得到相关性方程：

t=6.3290X-5.7255X+8.4585Xc-

0.815E1-0.663E2-2.206E3-2.838，

(1)

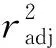
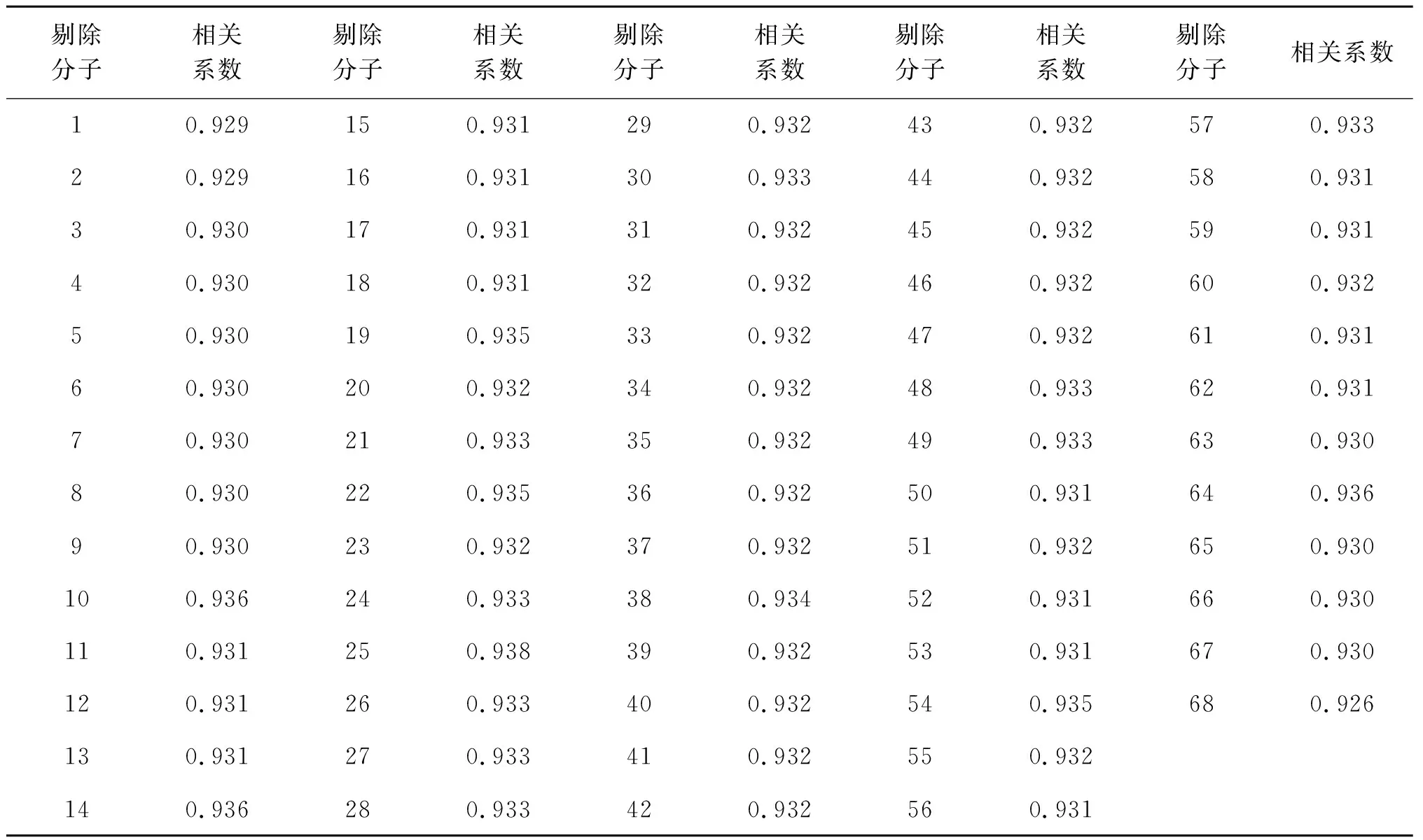
表2 Jackknifed相关系数的检验

对这68个相关系数作直方图(见图1)，Jackknifedr基本呈正态分布；为检明乌药化学分子中是否存在“离域”的色谱保留时间，对68个相关系数以0.920为圆心，0.002为间距作雷达图(见图2)，68个Jackknifedr值均落在区间内，说明模型不存在异常的保留时间值.

2.2 模型的建构

以优化筛选的连接性指数(0X，5X，5Xc)和电性拓扑状态指数(E1，E2和E3)为神经网络的输入变量，以湖南产乌药化学成分的色谱保留时间为输出变量，综合Andrea和文献[20]中2种隐含层变量选择规则，得到：

2.2>N/M≥1.4,

(2)

其中，N为总样本数，M为总权重，计算公式为

M=(Im+1)Hi+(Hi+1)Ou，

(3)

其中，Im，Hi，Ou分别为神经网络三层结构中输入层、隐含层和输出层的变量数. 这里，输入层变量数Im=6，保留时间作为输出层变量数Ou= 1，故隐含层变量Hi可取4或5.经比较，当Hi取5时，模型的相关系数值最大，故本模型采用6∶5∶1的网络结构，隐含层采用tansig传递函数，输出层采用purelin传递函数，迭代次数为3 000次.

为防止“过训练、过拟合”，在数据运算过程中，将68种化学成分分为训练集(以每5个分子作为一组，

图1 Jackknifed相关系数r的直方图Fig.1 Histogram of correlation coefficent r

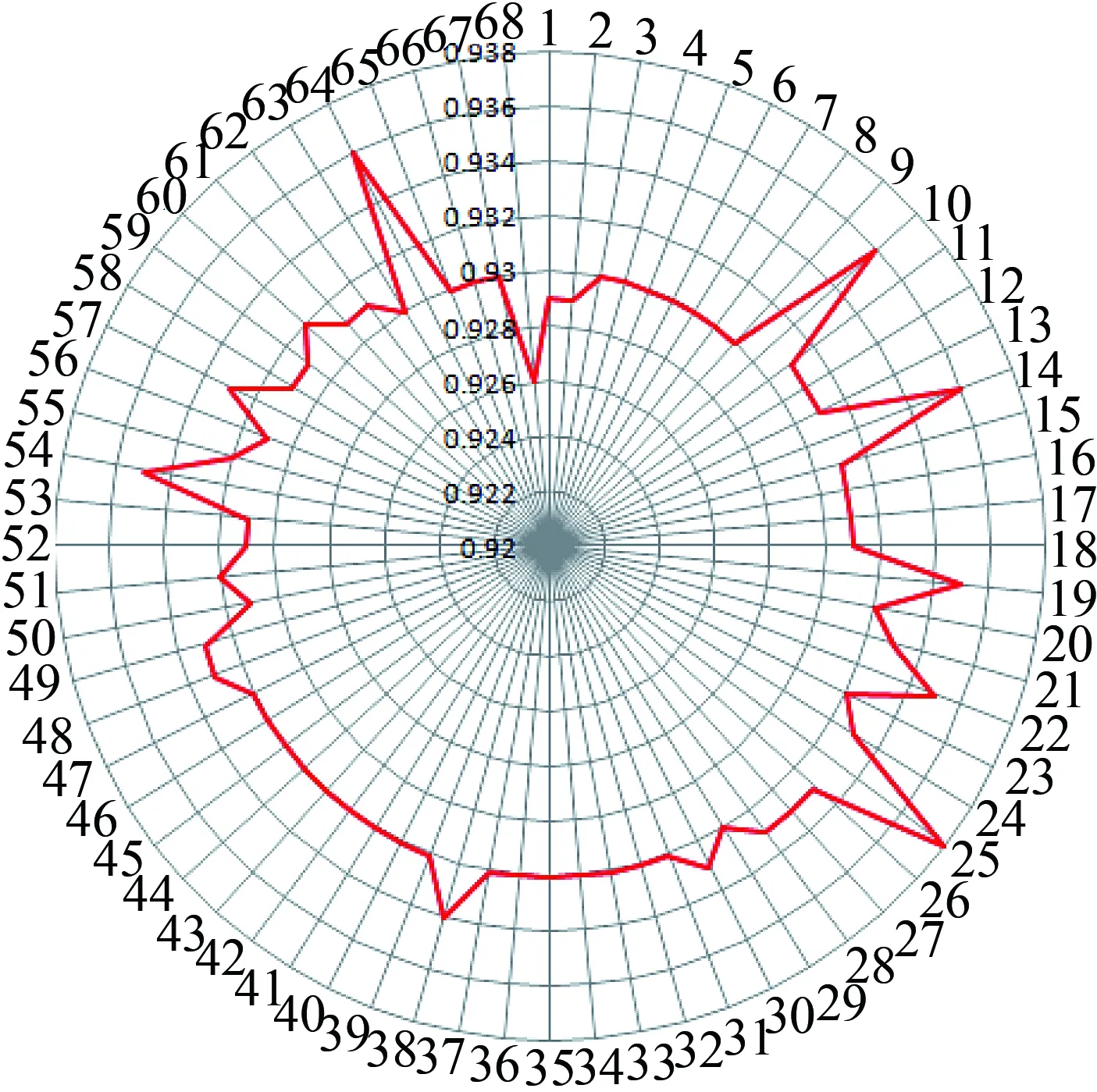
图2 Jackknifed相关系数r的雷达图Fig.2 Radar map of Jackknifed correlation coefficent r

取其中第1，3，4个分子)、测试集(取每组的第2个分子)和验证集(取每组的第5个分子，依此类推)，对其进行神经网络法分析，模型总相关系数rt达0.994 0，相关性较高，训练集相关系数r1达到0.992 9，测试集相关系数r2达到0.997 0，验证集相关系数r3达到0.997 9，可以看出，训练集、测试集、验证集的相关系数与总相关系数较为接近，利用该神经网络模型预测得到的乌药化学成分的色谱保留时间与文献方法分析检测的实验值吻合度较高，平均相对误差为2.66%，预测值与实验值关系见图3.图3中无特别远离直线的点，说明预测值较接近实验值.

图3 保留时间的实验值与预测值的相关性Fig.3 Relationship between experiment and predicted values of t

3 结果与讨论

乌药因具有多种抗炎、抗氧化、抗肿瘤的活性成分，成为越来越多研究者关注的热点. 大量研究证实，乌药含有丰富的呋喃倍半萜及其内酯、黄酮、生物碱、挥发油等成分，由于成分较为复杂，难以用实验方法对其性质一一研究. 为此，本文通过计算乌药化学成分的分子连接性指数和电性拓扑状态指数，筛选出能反映分子空间结构信息的3种连接性指数(0X、5X、5Xc)，以及能反映电子结构信息的3种电性拓扑状态指数(E1、E2、E3)，结合这6种指数构建BP神经网络模型，能很好地反映乌药化学成分色谱保留时间的变化规律.

当外部检测条件一定时，本模型中的3种连接性指数(0X、5X分别代表0价、5价的路径指数，5Xc代表簇项指数)说明碳原子的个数以及原子之间的连接方式对保留时间有影响；3种电性拓扑状态指数(E1代表“—CH3”基团的取值，E2代表“—CH2—”基团的取值，E3代表“>CH—”基团的取值)则说明分子中伯、仲、叔碳原子对保留时间有影响，但同样是伯碳原子、仲碳原子或叔碳原子，由于所处位置不同，原子之间的相互作用力就不同，各性质特征值也不同，因此，只有将连接性指数与电性拓扑状态指数相结合构建的模型，才能反映这一规律. 从表1所列的分子及保留时间可以看出，当检测条件固定时，碳原子及基团的数量、连接方式、范德华作用力、色散力、诱导力等均对保留时间产生影响，当碳原子数增加时，分子体积增大，色散力增大，保留时间延长.

筛选出的分子结构指数与乌药化学成分的色谱保留时间呈高度的非线性关系. 本文根据分子拓扑结构、电性结构特征构建的神经网络模型，有良好的稳定性，预测能力较强.对预测湖南产乌药化学成分的色谱保留时间、探索色谱保留机制、选择合适的色谱条件有一定的指导作用.