改进集合平方根滤波的目标跟踪算法∗
张家叶子 吕 游 王华松
(1.92941部队 葫芦岛 125000)(2.91899部队 葫芦岛 125001)
1 引言
在非线性的系统模型中滤波算法包括扩展卡尔曼滤波(EKF)、集合卡尔曼滤波(EnKF)、集合平方根滤波(EnSRF)和粒子滤波等。其中,集合平方根滤波[1]采用了相关统计信息的低秩表示,计算简单。粒子滤波的不限制系统和测量模型或噪声的分布情况,自举滤波器和辅助自举粒子滤波器[2~6]则基本解决了粒子滤波中粒子的多样性问题。
2 系统模型
在本文中,我们采用了一个未知转弯率的坐标转弯模型[7],目标状态向量 xk由 [ ]xk,x˙k,yk,y˙k表示,xk,yk表示代表目标的坐标,x˙k,y˙k代表目标在x和y方向的速度。转弯率为状态向量中的未知参数,需要在每一个时刻进行估计。系统模型为
T为采样间隔。Ω代表转弯率,是目标速度的非线性函数,模型是非线性的。以转弯率为扩展状态的状态向量可表示为
系统转移函数表示为
假设测量设备定位在原点使观测值由方位角测量模型化:
多个观测值来自不同的目标和杂波,每一个获得的测量值或者关联到一个目标,或者被视作无效测量值而丢弃。本文改进了联合概率数据关联(JPDA)技术[8~9]。
3 滤波技术
在目标跟踪中,通过随机滤波算法估计单目标的状态。自举滤波器一般由贝叶斯递归滤波实现。自举滤波器的主要缺点是,当所估计的PDF分布不均时,需要更大的粒子数。辅助自举滤波器使用辅助变量来帮助选择最具代表性的粒子,在低过程噪声的情况下性能较自举滤波器有很大提高。
3.1 集合平方根滤波器EnSRF
集合平方根滤波器EnSRF[10]是从集合卡尔曼滤波器(EnKF)导出的。它的主要优点是对涉及的统计信息的低秩表示。平方根滤波器通常使用一些非唯一变换将预测相位参数变换到分析相位参数。在EnSRF中,m成员集合称为{xi,(i=1,…,m)},用于表示n维状态空间。在滤波器中使用的集合均值由下式给出:
集合扰动矩阵实际上是集合协方差矩阵的矩阵平方根。EnSRF具有处理传达集合统计信息的低维扰动矩阵的优点。
EnSRF涉及预测阶段和分析阶段,,预测步骤与在粒子滤波中执行的预测相同。预测观测集合定义为
分析参数为
如果预测和观测模型是线性的,当m→∞时上面给出的更新方程收敛到传统的卡尔曼滤波。
3.2 带粒子更新的集合平方根滤波器
带粒子更新的集合平方根滤波器[11]是EnSRF的变体,集合通过EnSRF的分析阶段传播。它的优点是在每个时间步骤的集合分析中都不依赖于高斯分布假设。分析集合可以从预测集合获得:
i代表集合的索引。在EnSRF中,它是预测集合的平均值,有助于分析整体平均值,但在本算法中,它的每个元素都用在分析中起到作用。
3.3 基于样本的联合概率数据关联
本文中使用基于样本的联合概率数据关联[12]来消除测量源的不确定性,基于联合概率的数据关联被集成到用于状态估计的粒子滤波器中。这里,将各样品用元组(n,n)代表,是重要性因子或与状态相关的权重。在基于联合概率的数据关联中估计权重 βji,表示测量j属于目标i的概率。在基于样本的联合概率数据关联中,该因子由下式给出:
θ表示联合关联事件,唯一地确定每个观测值到其相应目标之间的关联。mk表示已经验证的测量数量,α是归一化因子,γ表示观察到的测量是虚假值的概率。一旦分配概率可用,则样本的权重被计算为
3.4 基于样本的联合概率数据关联和带粒子更新的集合平方根滤波器
所获得的分配概率βji可以并入带粒子更新的集合平方根滤波器框架中来保管多个目标观测值。采用基于样本的联合概率数据关联分析粒子:
这种权重改变将强化更新中最恰当测量的作用,同时降低所有其他测量的影响。
4 仿真实验
本文实验的目标跟踪工作是在对三个滤波器进行模拟和比较,主要是自举滤波器,辅助自举滤波器和带粒子更新的集合平方根滤波器。
轨道遵循协调转弯模型,对于粒度为50模拟绘制30个时间步长的结果。轨道的初始位置坐标取为(-5,-4),相应的初始转弯率别为0.7。
绘制100蒙特卡洛运行的均方根误差(RMSE)和样本方差,并用于比较三个滤波器的性能。图1和图2示出了自举滤波器,辅助自举滤波器和本文的方法的跟踪性能。从这些曲线图可以看出,与自举滤波器和辅助自举滤波器相比,本文的方法显示出优越的跟踪性能。轨迹的RMSE图如图3所示。与其他两个滤波器相比,本文的方法具有最低的RMSE值。辅助自举过滤器的RMSE性能高于自举过滤器。
从样本方差图看出,本文方法在所有给定的图示中清楚地给出最低RMSE值,并给出一致的跟踪性能。虽然辅助自举滤波器的性能比自举滤波器更好,但是比本文方法和自举滤波器速度慢。表1中比较了三种滤波器的执行时间。自举滤波比本文的方法快,但其跟踪性能差。因此,本文的方法可以说是对当前问题的一个更快、更准确的解决方案。
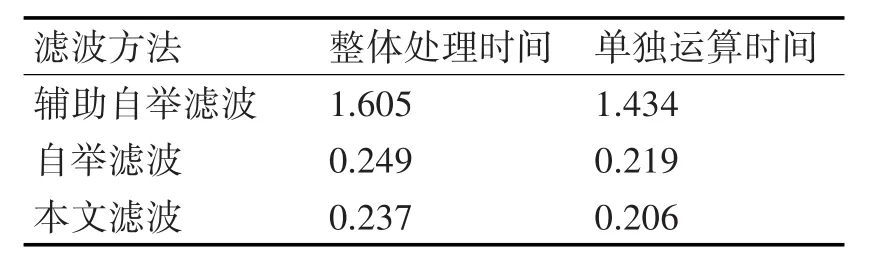
表1 执行时间
5 结语
本文通过将基于样本的联合概率数据关联纳入状态估计算法来实现数据关联。将提出的滤波器的结果与自举滤波和辅助自举滤波算法进行比较,实验结果表明,与自举滤波和辅助自举滤波相比,所提出的融合基于样本的联合概率数据关联和集合平方根的滤波检测结果更加准确,数据关联更加有效,运算简单,速度更快,提供相同的跟踪性能所需的总体粒度比由自举滤波和辅助自举滤波小得多。

