政府补贴模式与产学联盟内部企业研发响应策略
——基于演化博弈模型的仿真分析
王昳玢,潘祺志
(1.东北财经大学 经济学院,辽宁 大连 116025;2.包头师范学院 经济管理学院,内蒙古 包头 014030)
一、引 言
政府对企业研发的补贴源自于研发活动的正外部性所导致的私人研发投入意愿的不足,以及在一些关键技术的创新中普遍存在的市场失灵现象[1]。即使世界上大多数国家都对本国企业研发进行不同程度的补贴,所谓的“最优激励策略”或“最优补贴模式”依然是一个存在争议的问题。政府补贴模式的选择困境在于:基于成本补贴性质的事前补贴存在企业道德风险的可能,即企业具有夸大研发活动的技术前景及社会收益以骗取补贴的动机。而奖励性质的事后补贴虽然能够提升政府资金的激励效应,但对研发创新的市场失灵现象纠偏能力明显较弱[2],不利于在一些涉及国家创新战略的关键技术上保证足够的企业研发激励强度。对此问题的解决策略集中在政府的完全监督上,即有效的技术甄别与研发检测[3];建立赔偿威胁以及合作承诺维系的约束机制[4];具备约束力的政府参与的研发联盟[5]。但考虑到信息不对称、复杂技术创新的不可预测性,即使忽略政府技术甄别能力与监督成本的影响,完全监督也是不可能的,原因在于完全监督的社会扭曲成本将是难以接受的[6]。因此,不同技术特征与研发情景下的相对补贴策略有效性问题逐渐成为相关研究的重要分支。
随着产学联盟等不同形式的研发合作体逐渐成为创新研发的主要载体,包括囚徒困境、弱化合作困境的鹰鸽博弈及牡鹿博弈分析开始广泛用于分析企业的合作与非合作行为[7],并在研发企业机会主义存在前提下对产学联盟研发企业的针锋相对策略、背叛与宽恕策略等提供解释[8]。特别是在有限理性假设下,易余胤等[9]开始基于演化博弈模型研究产学联盟企业的模仿、学习、合作及竞争行为的变化过程,从而对研发合作策略的试错性、局部最优性及跟随性给出了更准确的分析。并且逐渐从无名氏定理拓展到随机匹配博弈和多边随机匹配合作博弈中,进而从合作研发企业的“信任”和“承诺”[10]、“契约交互关系”[11]等层面分析竞争与合作、承诺与背叛策略的出现。
但到目前为止,仅有极少的文献关注于政府补贴模式与产学联盟研发企业策略的关系,而在演化博弈框架下探讨政府激励与研发策略调整的文献就更为匮乏。实际上,作为研发主体的企业,其既有强化研发合作以降低技术和创新收益不确定性的意愿,存在积极响应政策提升社会声誉的诉求,也存在相机抉择及有限跟随以控制研发投入的策略分布[12]。同时,政府特别是地方政府在属地政策收益最大化目标及补贴资金稀缺性的约束下,期望通过有效的补贴策略能够激励企业参与产学联盟平台进行合作研发以实现创新能力改善的战略目标。另外也有通过非合作及背叛式的竞争性研发强化企业研发竞争,形成创新竞标赛格局的刺激意愿。因而产学联盟企业研发策略具有典型的学习、观察、模仿特征,符合演化博弈的基本分析范式。正是基于这样的考虑,借鉴Press和Dyson[10]提及的产学联盟企业间协同性的软约束所导致的机会主义倾向,本文构建研发企业“承诺维系下的合作”以及“背叛发生时的竞争”两种情景,并在双寡头博弈框架下分析不同情景下企业参与和不参与产学联盟研发的策略变化。同时,将政府补贴模式纳入到企业研发决策分析中,以考察不同政府补贴模式对产学联盟企业研发决策的影响及作用路径,进而探讨不同情景下的最优补贴模式,最后基于仿真分析进一步验证理论分析。
二、不同政府补贴模式下的产学联盟企业研发决策博弈模型
(一)基本假设
在双寡头博弈前提下,假设某项技术创新仅有企业A与企业B两家参与,技术创新的产品收益为r,技术研发成功系数为η,则研发成功后的总收益为ηr,技术创新所需的研发投入总成本为i,企业间不存在市场地位差异因而能够平均共享技术创新红利。同时,假定技术研发成功系数由技术的复杂程度决定,但与研发参与企业数量无关。
在该新技术的研发上,可供选择的学研机构是不唯一的,此时分为两种情景:一是“承诺维系下的合作”,即研发企业与一家学研机构组成共同的产学联盟;二是“背叛发生时的竞争”[注]实际上,背叛并不必然地导致竞争。在具体的研发合作体中,研发企业的策略可以细分为总是合作、针锋相对、绝不宽恕以及宽恕下的针锋相对等不同类型。本文为简化分析过程仅讨论了合作与背叛出现时的不合作两种策略,即认为研发企业表现出典型的“短视性”,一旦背叛出现将立即终止合作。,指企业A与企业B分别与不同的学研机构组成各自的产学联盟。其中,“承诺维系下的合作”是由于企业A与企业B均可预期到合作策略下由于成本共担企业各自投入的研发成本仅为i/2,同时企业研发的互补性优势较为突出[13],此外也存在政府所建立的一种维系合作关系的约束或奖励机制,从而强化了企业的合作意愿。而“背叛发生时的竞争”则是由于承诺维系的政府约束力度弱、垄断性创新红利的制度保障强度低及技术模仿成本低,因而出现研发合作中机会主义策略收益偏高进而导致合作的破裂与背叛的发生。具体到两种情景的转换概率,其取决于研发合作中机会主义与道德风险的收益成本分布[14]、专利保护强度、政府针对合作的约束力度、研发互补性及吸收能力差异[15]。
在两种情景中,企业A与企业B的策略选择集中在是否参与产学联盟进行技术研发,即企业的策略空间均为[参与,不参与],企业参与产学联盟将产生新增收益Δr与新增成本Δi。新增收益主要来自与学研机构合作带来的知识共享效率提升,而新增成本则为产学联盟合作的知识共享成本,包括技术购买、信息交换等环节的费用增长。因此,在“承诺维系下的合作”情景下,不参与策略变化为不参与、不合作,此时企业A与企业B均进行封闭式研发,研发收益ηr共享,同时需各自投入研发成本i。参与策略下,研发收益ηr+Δr共享,研发投入成本共担,同时新增成本Δi由两家企业分摊。在“背叛发生时的竞争”情景下,不参与策略也是不参与、不合作,企业A与企业B的独立研发收益共享,成本均需投入i。而参与策略下,企业A与企业B均选择与研发机构单独构建产学联盟,企业间形成事实上的竞争性研发关系,此时研发收益ηr+Δr共享,初始研发投入成本i不变,但各自负担额外投入成本Δi。
假设政府补贴策略分为事前补贴与事后补贴,政府补贴为c,在“承诺维系下的合作”情景下,政府补贴无论何种补贴模式均由企业均分。而在“背叛发生时的竞争”情景下,政府事前补贴由研发企业均分,而事后补贴则由实现研发目标的企业唯一获取,失败或落后的企业将无法得到政府补贴。同时,假设政府补贴、产学联盟的新增收益与新增成本变化均为外生变量,即政府补贴模式与补贴强度并不改变产学联盟的新增收益与新增成本。
(二)“承诺维系下的合作”情景下的企业研发决策动态博弈
根据上文的基本假设,在“承诺维系下的合作”情景下,两企业之间合作的创新收益矩阵如表1所示。

表1两企业之间合作的创新收益矩阵
假设企业A选择参与策略的概率为x,则选择不参与策略的概率为1-x;企业B选择参与策略的概率为y,同理选择不参与策略的概率为1-y。
根据苏先娜和谢富纪[16]的研究,此时企业A的研发收益可表示为:
(1-y)
(1)
(2)
(3)

(4)
故企业A的复制动态方程为:
(5)
同理,企业B在不同研发策略下的研发收益函数同样可表示为:
(1-x)
(6)
(7)

(8)

(9)
故企业B复制动态方程为:
(10)

根据Friedman[17]的研究,演化系统的均衡点的稳定性可由其雅可比矩阵的局部稳定性分析得到。
由式(1)和式(2),则雅可比矩阵J为:
(11)
上述雅可比矩阵行列式值和迹的符号如表2所示。

表2系统演化稳定结果
由表2 可知,五个均衡点中O(0,0)和V(1,1)是ESS点,W(0,1)和U(1,0)是不稳定点,S(x,y)是鞍点。其中演化稳定点O(0,0)表示,在“承诺维系下的合作”情景下,若其中一个企业选择不参与产学联盟合作研发,则另一个企业也将选择不参与,此时企业博弈结果为ESS 点O(0,0),即[不参与,不参与]策略。但若某个企业打破该稳态均衡,选择参与策略,则对另一个企业而言,由于合作约束前提下能够共同承担合作研发新增成本Δi,故也会选择参与策略,此时博弈结果为ESS点V(1,1),即[参与,参与]策略。
在研发企业的2×2策略空间中,其参与策略的动态演化过程如二维相位图1所示。

图1 “承诺维系下的合作”策略动态演化图
由图1 可对企业合作技术创新博弈动态过程进行分析。由两个不稳定点W和U 与鞍点S 连成的折线W-S-U 为博弈双方不同状态的临界线。初始状态在折线右上方区域Ⅱ (WSUVW),系统将收敛于ESS点V(1,1);初始状态在折线左下方区域 S (WSUOW),系统将收敛于ESS 点O(0,0)。
企业A 与企业B长期演化博弈的结果是 [参与,参与]策略或是[不参与,不参与]策略,取决于图1中的sI和sII大小。若sI=sII,采用[参与,参与]的概率与[不参与,不参与]的概率相等。若sI 也就是说,在“承诺维系下的合作”情景下,企业的研发策略取决于合作研发的增益Δr、合作成本Δi以及研发总成本i的大小。当Δr>Δi时,企业将向ESS点V(1,1)稳态收敛,此时企业决策为[参与,参与]。而当Δr<Δi时,企业博弈结果将收敛于ESS点O(0,0),此时企业决策为[不参与,不参与],且合作研发新增收益Δr越大,企业参与合作研发的概率越高。 这意味着,在考虑政府补贴的前提下,无论是事前补贴模式还是事后补贴模式,在企业均分的预设前提下政府补贴c的存在实际上等于形成了研发收益的净增长与直接的成本补贴,因而其对企业的研发策略不存在激励差异,此时事前与事后都是有效的政府补贴模式。同时,从合作研发激励看,企业存在参与、不参与的策略转换阈值。当Δr>Δi或Δr<Δi且Δr+c>Δi时,演化博弈将出现[参与,参与]的静态纳什均衡,即政府补贴强度只要能够保证企业研发收益i为正,就能够实现合作研发激励。 在“承诺维系下的合作”情景下,企业策略表现出典型的策略跟随趋势,一个企业的参与策略将促使[参与,参与]稳态均衡的出现。考虑到我国政府创新制度设计具有较为突出的“优势企业扶持策略”特征[注]“优势企业扶持策略”是Aghion等[18]在对东亚新兴市场国家增长奇迹的观察基础上提出的,用以描述这些国家集中对一些重点企业的扶持,包括信贷、税收、产品市场保护等政策倾斜,以加速企业资本形成速度与规模优势,从而基于垄断有利于创新的理论前提形成事实上的创新激励。,那么集中针对优势企业的政府补贴也能够形成相应的合作研发激励。但这种区别对待的产业政策可能会形成事实上的政策歧视,从而放大优势企业的道德风险,也不利于合作承诺的维系。因此,基于技术研发的“项目式”而非基于研发个体的“企业式”补贴策略才更有利于产学联盟的形成以及企业合作研发的激励。 再考虑由于合作研发中的机会主义倾向、较弱的研发红利公平分配机制等因素导致背叛出现的情景。在“试错性”与“短视性”的研发策略调整中,一旦某个企业表现出机会主义倾向,则背叛的发生将使企业合作承诺难以维持。此时企业研发状态转换为“背叛发生时的竞争”,由于存在两个产学联盟参与研发,因而每个产学联盟的新增收益Δr减半,但新增成本Δi不变。 在这种情景下,若企业A参与的策略概率依然为x,企业B相应的选择参与策略概率为y,则两企业之间非合作的创新收益矩阵可如表3所示。 表3两企业之间非合作的创新收益矩阵 此时,企业A的研发收益可表示为: (12) (13) (14) (15) 故企业A的复制动态方程为: (16) 同理,在“背叛发生时的竞争”情景下,企业B的研发收益为: (17) (18) (19) (20) 故企业B复制动态方程为: (21) 同理,其雅克比矩阵为: (22) 由式(22)可知,企业A与企业B的博弈收益水平高度依赖于Δr-Δi的符号,以下本文分别针对Δr-Δi>0和Δr-Δi<0进行演化分析。 首先,给出约束条件Δr-Δi>0下的博弈策略演化过程如表4所示。 表4 Δr-Δi>0系统演化稳定结果 由表4可知,4个均衡点中V(1,1)是ESS点, O(0,0)是不稳定点,W(0,1)和U(1,0)是鞍点。当Δr-Δi>0时,在产学联盟竞争性策略约束下,博弈双方基于自身利益最大化目标,将一致性地选择[参与,参与]策略,最终双方博弈结果收敛到ESS点V(1,1)。用二维相位图来描述表4条件下的动态演化轨迹如图2所示。 图2 Δr-Δi>0时系统动态演化图 其次,在约束条件Δr-Δi<0下的博弈系略演化过程如表5所示。 表5 Δr-Δi<0系统演化稳定结果 由表5可知,四个均衡点中O(0,0)是ESS点, V(1,1)是不稳定点,W(0,1)和U(1,0)是鞍点。实际上,在“背叛发生时的竞争”情景下,由于企业参与产学联盟需独立负担合作研发新增成本Δi,大于合作新增收益Δr,故企业必然选择不参与策略,此时博弈收敛到ESS点O(0,0),企业策略为[不参与,不参与]。用二维相位图来描述表5 条件下的动态演化轨迹如图3 所示。 图3 Δr-Δi<0时系统动态演化图 最后,考虑在“背叛发生时的竞争”情景下,政府补贴模式的差异对企业研发决策的影响。在事前补贴模式下,政府补贴的激励效应主要通过改变研发收益与研发成本而实现。考虑到Δr-Δi的符号决定了企业均衡的研发策略结果,因而政府补贴强度只要能够实现c+Δr>Δi,即可保证竞争性产学联盟的形成。虽然此时研发活动整体的企业损益与社会福利水平相对于“承诺维系下的合作”出现了一定损失,但竞争性产学联盟的出现能够保证政府补贴达到预期的创新激励目标。同时[参与,参与]纳什均衡解的存在说明“优势企业扶持策略”导向下的事前政府补贴也是有效的。 但是,当政府选择奖励性的事后补贴模式时,政府补贴在改变了研发收益与研发成本的同时,形成了事实上的企业研发竞争。因而企业的研发成功系数就不再由技术复杂度唯一决定,而还取决于是否能够最快地实现研发目标。此时将使得企业预期的研发成功系数下降,在总成本不变的前提下,这实际上等于降低了企业的可预期研发收益,即在Δi不变的前提下降低了新增收益Δr。而且企业的同质化程度越高,企业研发能力与技术吸收能力越接近,研发成功系数的变化越大,奖励性的事后补贴对研发收益的影响越强。这将形成“背叛发生时的竞争”情景下,企业研发决策从[参与,参与]向[不参与,不参与]转换的逆向激励效应。而且在机会成本决策模式下,这种扭曲激励效应会随着政府补贴强度的上升而增强,此时对产学联盟的形成将产生较大的不利影响。因此,在“背叛发生时的竞争”情景下,事前补贴才是更优的政府激励策略。 为了分析上述演化博弈过程中初始概率水平、产学联盟合作研发的新增收益Δr、合作研发新增成本Δi以及研发投入成本i的变化对企业间参与与不参与的策略影响,本文进行了“承诺维系下的合作”与“背叛发生时的竞争”两种情景下企业收益函数动态方程的数值仿真模拟分析,以考察初值设定的调整对策略均衡实现的影响。 1.Δr变动对企业研发策略的影响 设定企业A与企业B的参与概率为x0=y0=0.3,取Δr渐变于区间[0.3,0.7],收益动态方程仿真结果如图4所示。 图4 Δr变动对演化结果影响的仿真 当产学联盟合作研发的新增收益Δr=0.3时,博弈双方处于参与与不参与策略的临界线,图中为一直线。当Δr>0.3时,博弈方基于产学联盟合作研发的收益增幅放大,企业选择参与策略的概率也进一步上升。同时,这种参与决策具有跟随效应,一家企业的参与将导致另一企业也转换为参与决策以共享收益,此时博弈双方趋于ESS 点V(1,1),即[参与,参与]策略。 反之,当Δr<0.3时,博弈方获取的合作收益较小,如果再考虑参与产学联盟的新增成本Δi,博弈方会放弃参与策略,转向不参与策略。同理,博弈的另一方也会选择不参与策略,这时博弈双方趋于ESS点O(0,0)。 仿真结果进一步证实,企业参与产学联盟的合作创新,其博弈策略与合作研发的新增收益Δr直接相关。因而,产学联盟是否能够形成取决于合作研发的收益、成本变化及政府补贴强度能够达到[参与,参与]策略均衡的触发阈值。 2.Δi变动对企业研发策略的影响 图5 Δi变动对演化结果影响的仿真 当合作研发新增成本Δi=0.25时,博弈双方处于[参与,不参]与策略转换临界线。当Δi>0.25时,博弈方参与产学联盟的合作净收益Δr-Δi减少,此时企业倾向于由参与策略转换为不参与。基于稳态ESS点具有策略同一性,此时另一博弈方也会选择不参与策略。这时博弈双方趋于ESS点O(0,0),即[不参与,不参与]。当Δi<0.25时,博弈方承担的合作新增成本Δi减少,从而导致了合作净收益增加,故博弈方趋于参与策略。同理,另一博弈方也会选择参与策略,这时博弈双方趋于[参与,参与]稳态。 总之,仿真结果进一步证实,在“承诺维系下的合作”情景下,企业研发策略与合作研发新增收益Δr以及合作研发新增成本Δi直接相关。考虑到产学联盟中知识与技术优势方的高校往往均具有正的显性收益,因而当前我国政府重点针对产学联盟中的企业进行直接补贴的政策是具有其合理性的,这种政策可以通过直接增大企业合作研发新增收益强化企业参与的激励。但由于Δr<Δi条件下,无论研发投入成本如何变化,企业均具有收敛于ESS 点O(0,0)的趋势,即不参与策略,因而政府补贴的实际激励效应还取决于政府补贴强度。只有通过补贴使得产学联盟企业研发损益条件由Δr<Δi转为Δr>Δi以达到参与策略触动阈值,这种激励效应才能显现。 在“背叛发生时的竞争”情景下,假设企业A与企业B的参与概率相等,即x=y,并设参与概率渐变于区间[0.1,0.6],取研发总成本i=2,则在不同的产学联盟新增收益、成本特征下,企业研发策略的演化路径如图6所示。 Δr>Δi Δr<Δi图6 Δr与Δi关系仿真 在“背叛发生时的竞争”情景下,当Δr>Δi时,由于企业单独参与产学联盟进行合作研发的净收益均为正,则无论初始概率水平如何,企业最终博弈的结果均收敛到ESS点V(1,1),此时企业均选择竞争性参与策略。反之,当Δr<Δi时,只有政府补贴选择事前补贴模式且补贴强度达到触发阈值,才能实现研发企业从不参与到参与的转移。 本文在双寡头研发框架下,利用演化博弈模型分析了企业在“承诺维系下的合作”与“背叛发生时的竞争”两种情景下企业参与产学联盟的策略演化过程,并考察了政府补贴模式的差异性激励效应,全文结论可归纳如下: 首先,在“承诺维系下的合作”情景下,企业是否参与产学联盟,取决于产学联盟合作的新增收益Δr、合作成本Δi以及研发总成本i的大小。当Δr>Δi时,企业均衡策略为[参与,参与],而当Δr<Δi时,企业均衡策略为[不参与,不参与]。同时,事前补贴与事后补贴的政府激励模式,不存在激励效应差异,均为最优的政策补贴模式。在是否能够形成产学联盟合作研发激励层面看,企业存在参与、不参与的策略转换阈值,即政府补贴强度只要能够保证企业的研发收益为正,就能够实现合作研发激励。 其次,在“背叛发生时的竞争”情景下,虽然产学联盟新增收益与新增成本的相对大小决定[不参与,不参与]与[参与,参与]策略的稳态均衡实现,但政府补贴模式在该情景下却表现出不同的激励效应。奖励性的事后补贴模式存在企业研发决策从[参与,参与]向[不参与,不参与]转换的扭曲激励效应,因而在“背叛发生时的竞争”情景下,事前补贴才是更优的政府激励策略。 最后,基于合作与非合作约束下企业收益函数的仿真分析进一步验证了博弈分析的结果。无论在合作还是非合作约束下,Δr的上升以及Δi的下降均能够增加企业进行参与策略选择的概率。研发净收益越大,企业参与产学联盟共享收益的概率就越大,否则企业选择不参与的概率就越大,但最终研发策略稳态均衡的出现取决于产学联盟研发损益变化及政府补贴强度。(三)“背叛发生时的竞争”情景下的企业研发决策动态博弈










三、企业研发决策演化博弈的仿真分析
(一)“承诺维系下的合作”情景下的演化博弈仿真分析

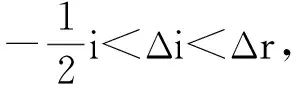

(二)“背叛发生时的竞争”情景下的演化博弈仿真分析

四、结 论

