Liquid Flow in a Porous Channel with Electrokinetic Effects∗
Hang Xu(徐航) and Huang Huang(黄煌)
Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration(CISSE),State Key Laboratory of Ocean Engineering,School of Naval Architecture Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China
AbstractIn this paper,a fully developed laminar flow in a porous channel between two paralleled flat plates in the presence of a double layer electric field is analyzed.The linear Poisson-Boltzmann equation is suggested to model the double layer electric field near the solid-liquid interface.The equation of motion is extended by including the electrical body force generating from the double layer field and then solved analytically.Different from previous models,our proposed one is continuous in the whole flow field and matches commonly-accepted models in the field of fluid mechanics.Besides,the effects of various physical parameters such as the zeta potential,the electrokinetic separation distance,and the ratio of the streaming current to conduction current on the velocity,the pressure,the apparent viscosity of the fluid,as well as the streaming potential are discussed.Physical explanations on the changing trends of those physical quantities with various parameters are given.
Key words:microchannel,expanding wall,porous wall,double layer electrical field,laminar flow
1 Introduction
Recently,researchers have found that liquid flows in various microchannels have many practical and potential applications in various systems such as Micro-Electro-Mechanical systems(MEMS)and microfluidics such as microchannel heat sinks for cooling micro-chips and laser diode arrays,Lab-On-Chip device for chemical and biomedical analyses,and microfluid pumps.
Some researchers have devoted them into the understanding the fundamental transport mechanisms of microchannel flow,typical work has been done by Eringen,[1]Pfahler et al.,[2]Mala et al.,[3−4]Ren et al.[5]Particularly,Xu et al.[6]noticed that the electro-viscous flow model used by Mala et al.[3−4]contains a wrong imposed boundary condition for the electrostatic potential in the center of the microchannel,which results in that the distributions of the electrostatic potential and velocity are discontinuous.They also noticed that the constant pressure parameter appeared in the papers of Mala et al.[3−4]and Ren et al.[5]is assumed to be known,which is incompatible with common used models for channel flows.[7−16]They then revised the model and applied it into a liquid flow of a microchannel driven by its upper moving wall and also by the double layer electrical field.
In this paper,we shall apply the revised mathematical model by Xu et al.[6]to the problem of liquid flow driven along a porous microchannel in the presence of electrokinetic effects.The problem is nondimensionalized and then solved analytically.The accuracy of the solutions is verifi ed.The variations of the velocity,the local skin friction,the pressure constant,the apparent viscosity,as well as the stream potential with different physical parameters are illustrated.The physical mechanisms regarding to the influences of various parameters on those physical quantities are discussed.
2 Solution of Poisson-Boltzmann Equation
As shown in Fig.1,the electrical double layer(EDL)denotes the arrangement of the electrostatic charges on the solid surface and the balancing charges in the liquid. Consider a flow containing positive and negative ions through a microchannel between two parallel positively charged plates.The channel walls undergo uniform injection or suction in the transverse direction.The uniform electrostatic potentials ϕ0are respectively imposed on both surfaces of the channel,which decrease gradually as they are away of the surfaces and minimize at the cross-section of the channel.The electrostatic potential ϕ at any point in the channel satisfies the Poisson’s equation
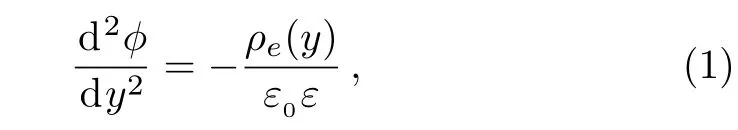
where ρeis the charge density,ε is the dielectric constant of the fluid and ε0is the permittivity of vacuum.
With the assumptions that the dielectric constant is uniform and the fluctuation is negligible,using the law of the equilibrium Boltzmann distribution,the number of ion distribution in a symmetric electrolyte solution is written as
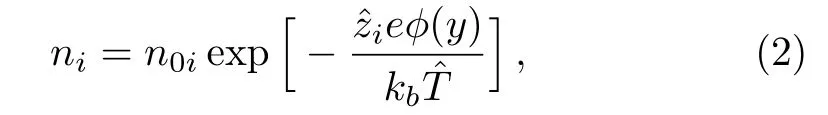
where n0iandare respectively the bulk ionic concentration and the valence of type i ions,e denotes the charge of a proton,kbis the Boltzmann’s constant,andis the absolute temperature.
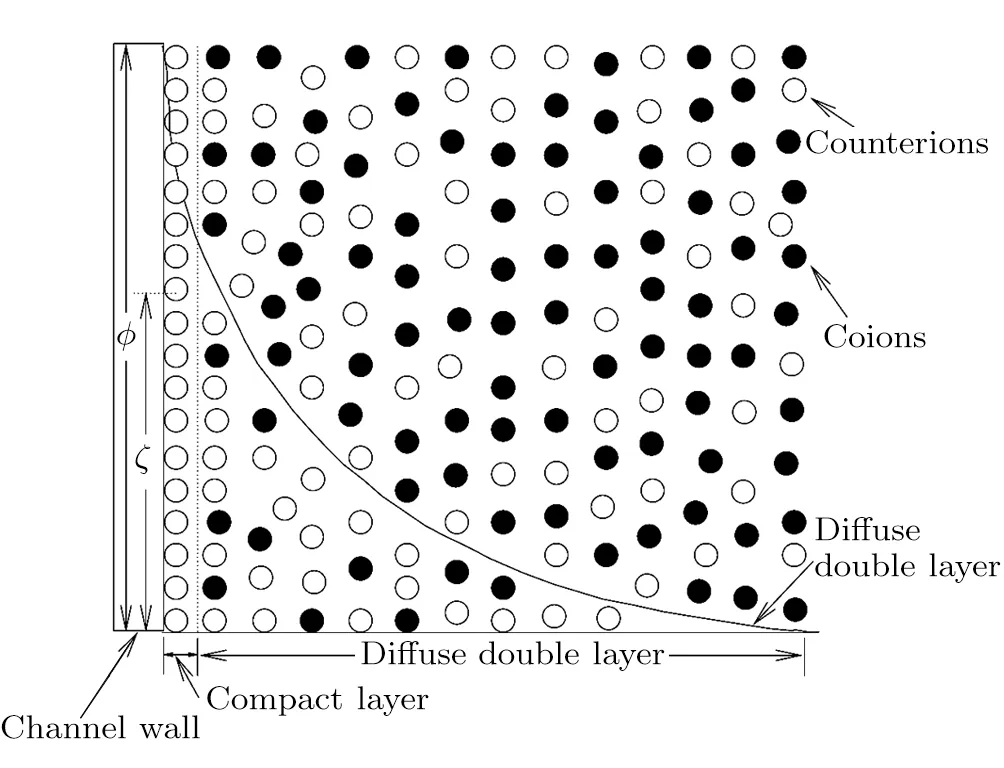
Fig.1 Physical sketch for electrical double layer at the channel wall.
On the other hand,the net charge density in a unit volume of the fluid is given,considering the Boltzmann equation,by
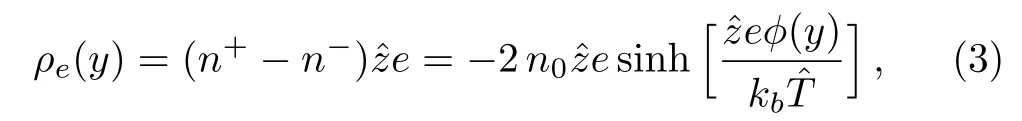
where n0is the average number of positive or negative ions andˆz is the valence of positive ions.
Substituting Eq.(3)into the Poisson equation(1),we obtain
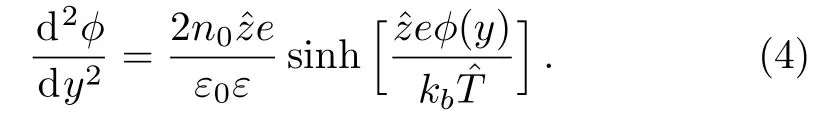
By defining the Debye-H¨uckel parameter as k2=/()with 1/k being referred to as the thickness of the electrical double layer(EDL),and then introducing the following dimensionless variables
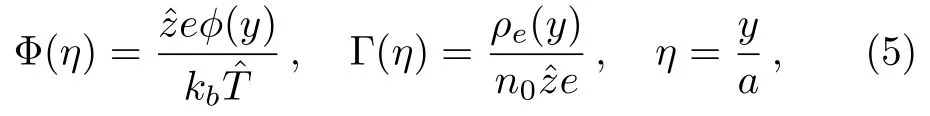
into Eqs.(1)adn(4),we obtain
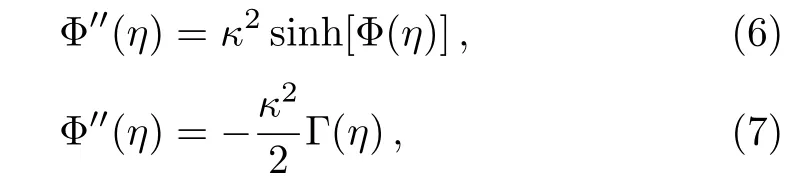
where κ=ak is a constant.The appropriate boundary conditions for this problem are given,taking account of the flow symmetry,by
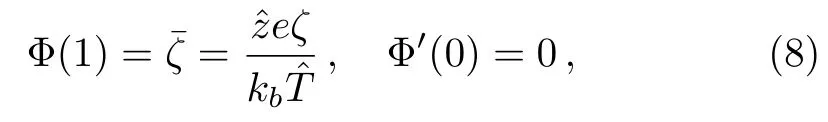
When the electrical potential is smaller than the thermal energy of the ions,i.e.,,we are able to use the Debye-H¨uckel linear approximation to transform Eq.(6)into
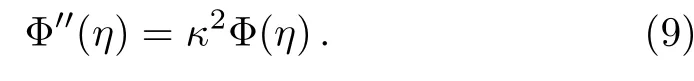
Equation(9)subjected to the boundary conditions(8)admits the following analytical solution
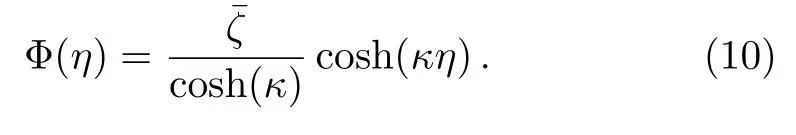
3 Equation of Fluid Motion
The two-dimensional fully developed laminar flow in a porous microchannel driven by the electric body force generated by the double layer electric field is graphically sketched in Fig.2,in which the y axis is perpendicular to the channel walls and the x axis is in a plane parallel to the channel walls.a is the half distance between the plates,L is the length of the plate.The following assumptions on the flow are enforced:(i)The fluid is incompressible;(ii)the flow is laminar and steady;and(iii)the fluid velocity leaving the channel walls is independent of position.

Fig.2 Physical sketch for microchannel flow.
Under those assumptions,the Navier-Stokes equations governing the flows are
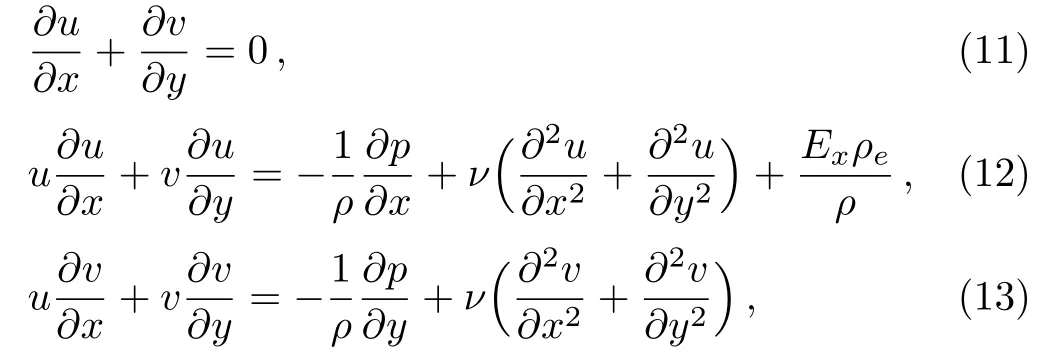
where u and v are the velocity in x and y direction respectively,ρ is the fluid density,p is the pressure,ν is the kinematic viscosity,and Exρeis the electrical body force.Note that the new term Exρeis generated by the electrical double layer(EDL),which is a structure near the wet surface of the microchannel.The EDL composes of two parallel layers of charge surrounding the microchannel.Thefirst layer is the surface charge(either positive or negative),which consists of ions adsorbed onto the object due to chemical interactions.The second layer is composed of ions attracted to the surface charge via the Coulomb force,electrically screening the first layer.It is made of free ions that move in the fluid under the influence of electric attraction and thermal motion.This model can be used to simulate flow in modern microfluidic systems where electro-kinetics(or electro-osmosis)plays a signi ficant role.It has more recently infiltrated into many sophisticated microscale designs including bio-chip systems for drug delivery,biomedical diagnostics and bio-microelectro-mechanical-systems(bioMEMS).
The associated boundary conditions are
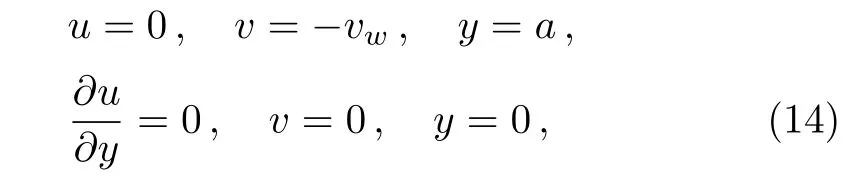
where vwis the injection or suction speed of the channel walls.
Define a stream function
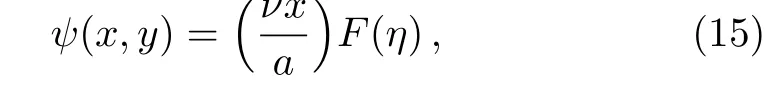
where
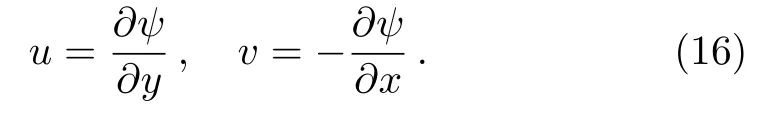
Non-dimensionalizing Eqs.(11),(12),and(13)via Eqs.(5)and(15),the continuity equation(11)is automatically satisfied,the rest equations are written,by emphasizing the pressure related terms,as
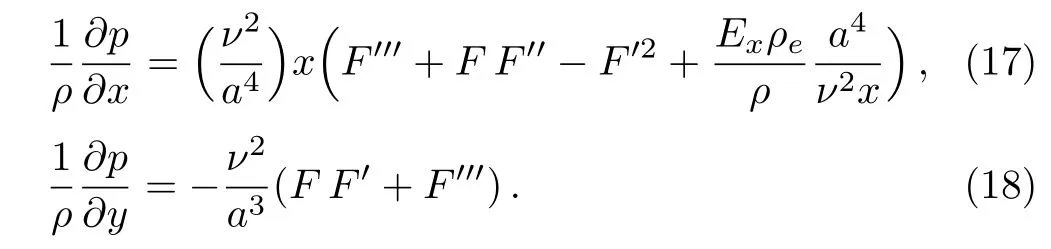
It is known that the right-hand side of Eq.(18)is independent of x,which implies ∂2p/∂x∂y=0.As a result,we obtain
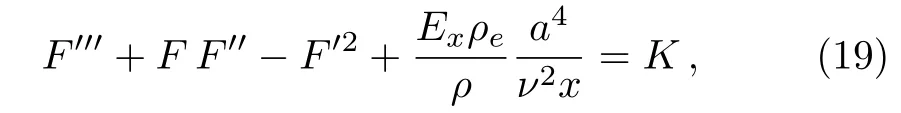
where K is an unknown constant.
By now,the electric field strength Exis not yet known,which can be obtained via balancing the streaming current against the electrical conduction current.[3−4]As is known that in the absence of an applied electric field,the streaming current is generated as a liquid is forced through a channel under hydrostatic pressure,which is defined by
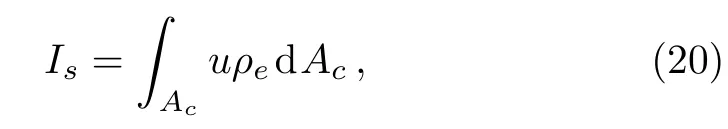
where Acis the cross-sectional area of the flow channel.
The streaming potential induces a conduction current in the opposite direction,which is given by
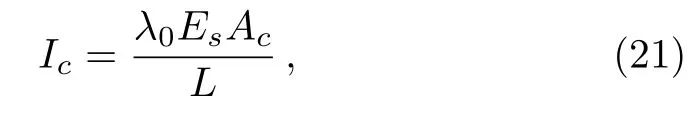
where λ0is the electrical conductivity of the fluid,Esis the streaming potential,and L is a reference length of the channel.
At the steady state,the net electrical current is zero,we therefore obtain
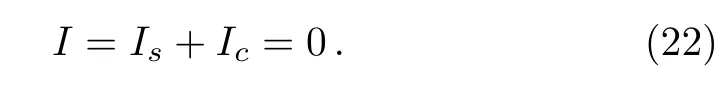
Substituting the above defined corresponding nondimensional variables into Eq.(22)via Eqs.(20)and(21),the following connection is established
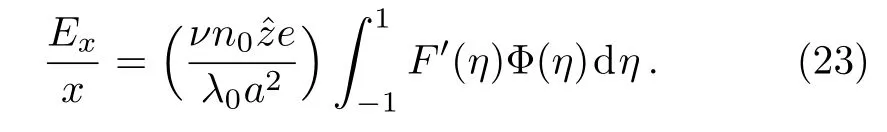
Since the terms of the right-hand side of Eq.(23)is independent of x,it is readily to know Exis proportional of x.The last term of the left-hand side of Eq.(19)can be transformed into
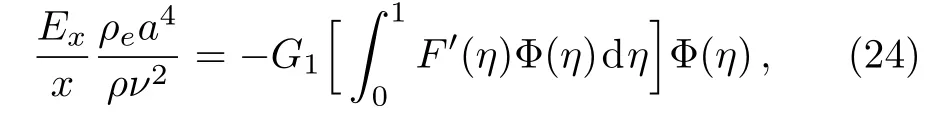
where
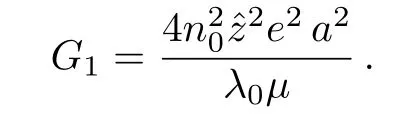
Therefore,Eq.(19)is reduced to
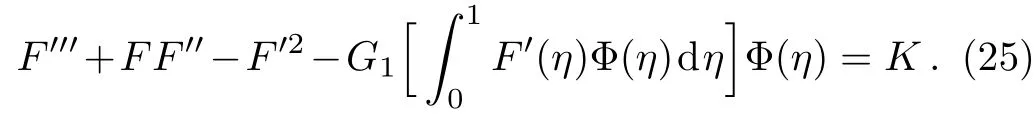
Due to Eq.(14),the boundary conditions for Eq.(25)are determined as
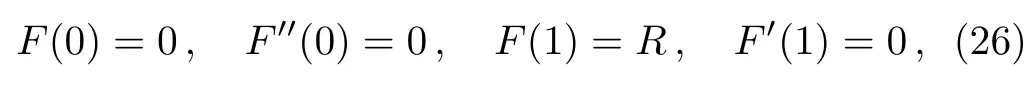
where R=vwa/ν is the Reynolds number.
4 Physical Quantities of Practical Interests
The volumetric rate of flow through the paralleled flat plates is computed via integration of the velocity distribution over the transversal surface as
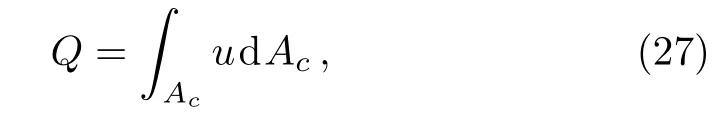
which is non-dimensionalized,by substituting the similarity variables(5)and(9)into Eq.(27),as
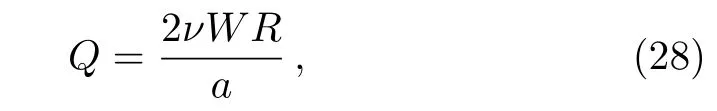
where W is the weigh of the channel.It is clearly seen that the volumetric rate of flow is independent on the EDL effect for this problem.
As is known that the motion of the ions in the fluid is restricted by the electrical force generated by the EDLfield.Therefore it is of great importance to evaluate the electro-viscous effect on the liquid flow.Besides the definition given in Eq.(27),it is also to measure the volumetric rate of flow of channel flow separated by a distance 2a via the following correlation(refer to Ref.[3])

whereµais the apparent viscosity taking account for the EDL effect.Taking account of Eqs.(17)and(25),Eq.(29)is written as
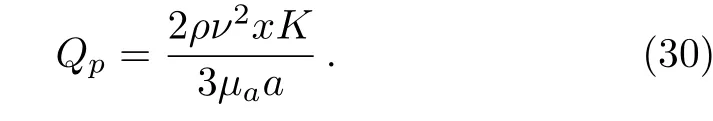
Equalizing Eq.(28)with Eq.(30),i.e.,Q=Qp,we obtain the ratio of the apparent viscosity to bulk viscosity as

The local skin frictional coefficient is important to quantify the flow phenomena in the microchannels and for the engineering design of microchannels,which is defined,for the upper surface,by

where

Substituting Eq.(33)into Eq.(32),we obtain
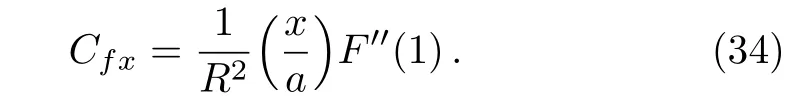
Define the local streaming potential Esas
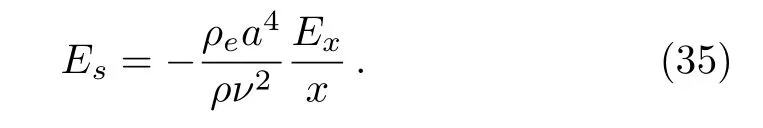
Using Eq.(23),we obtain
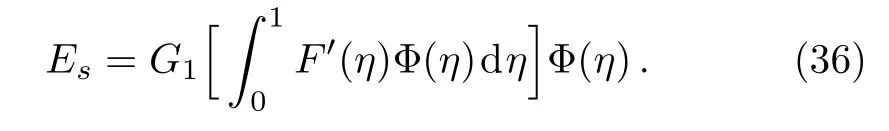
5 Result Analysis
The governing equation(25)subjected to the boundary conditions(26)is solved by the homotopy analysis method(HAM).[6]Since the technique has been available in literature,we omit the analytical procedure and just give the absolute error of our results,using the following correlation,
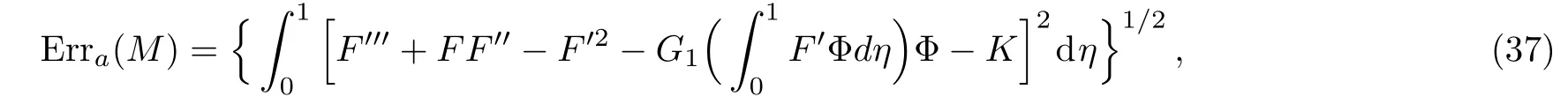
where M is the HAM computational order.Substituting different orders HAM approximations into Eq.(37),the absolute error at a certain order can be obtained.For example,the computational errors of various orders for the Reynolds number R=±5 are listed in Tables 1 and 2 respectively,very excellent convergence is found.

Table 1 Computational errors with different order Homotopy-Pad´e approximations under different values of κ in the case of ζ=1,R=20,and G1=10.

Table 2 Computational errors with different order Homotopy-Pad´e approximations under different values of κ in the case of ζ=1,R= −10,and G1=10.
As discussed in Ref.[6],the boundary condition of the electrostatic potential at the center y=0 given by Mala et al.[3−4]was wrongly imposed,which causes discontinuities for both the electrostatic potential and the velocity fields.To avoid their physically unrealistic assumption on this point,we adopt alternative assumption proposed by Xu et al.[6]for model refinement,in which the boundary conditions are only applied on both walls without constraint at the center y=0.
In the following we check the influences of various physical parameters on distributions of the velocity.It is shown in Fig.3 that the zeta potential¯ζ plays an important role on variation of velocity profiles.For both negative and positive Reynolds numbers,the increase of¯ζ is helpful to enhance the velocity profiles at the channel center,but leads to flow reversal near the side walls.Physically,the electric body force generated by the double layer increases with¯ζ enlarging,which assists the fluid motion.However,the increase of the velocity leads to the increase of the skin friction near the walls,which is opposite to the direction of fluid motion.As a result,theflow reversal near the walls occurs as grows sufficiently large.This trend is more clear as the Reynolds number R is negative.
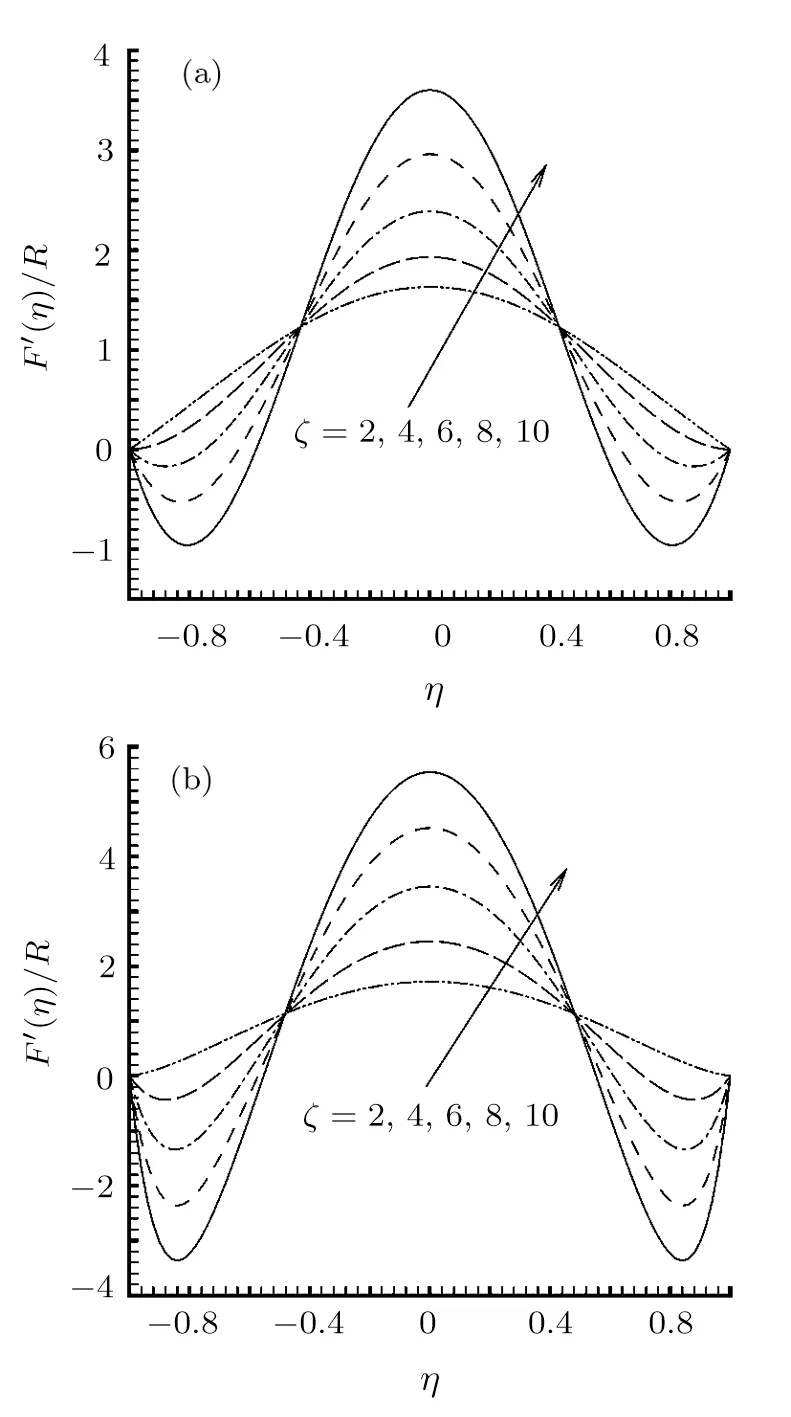
Fig.3 Distributions of the normalized velocity F′(η)/R for various values of ζ at κ =1 and G1=10.(a)R=5,(b)R=−5.
The electrokinetic separation distance κ also has significant effect on distribution of the velocity.As shown in Fig.4,the velocity profile decreases as κ increases.This is due to the double layer field exists only in the region close to the channel walls.When κ is adequately large,its effect is constrained into the thin double layer near the walls and almost has no effect on the flow far away from the walls.In this stage,the velocity distribution is almost same as compared with that without the EDL effects.On the contrary,when κ is small enough,the double layer field occupies considerable proportion of the channel cross-sectional area,its effect becomes predominant on fluid motion.Particularly,we notice for negative R,the flow reversal occurs as κ is sufficiently small.
The coefficient of the streaming potential G1,which characterizes the ratio of the streaming current to conduction current,is a key factor to affect the velocity distributions as well.As shown in Fig.5,the velocity profile at the center enhances as G1evolves.Again here the velocity variation for negative R is more obvious than that for positive one.Similarly,the flow reversal near the side walls appears as G1becomes sufficiently large for both the positive and negative Reynolds numbers.This indicates that the larger the G1,the more predominant is the effect of the streaming current caused by the double layer.Here the flow reversal is due to the skin friction force increases faster than the electric body force in the double layer.
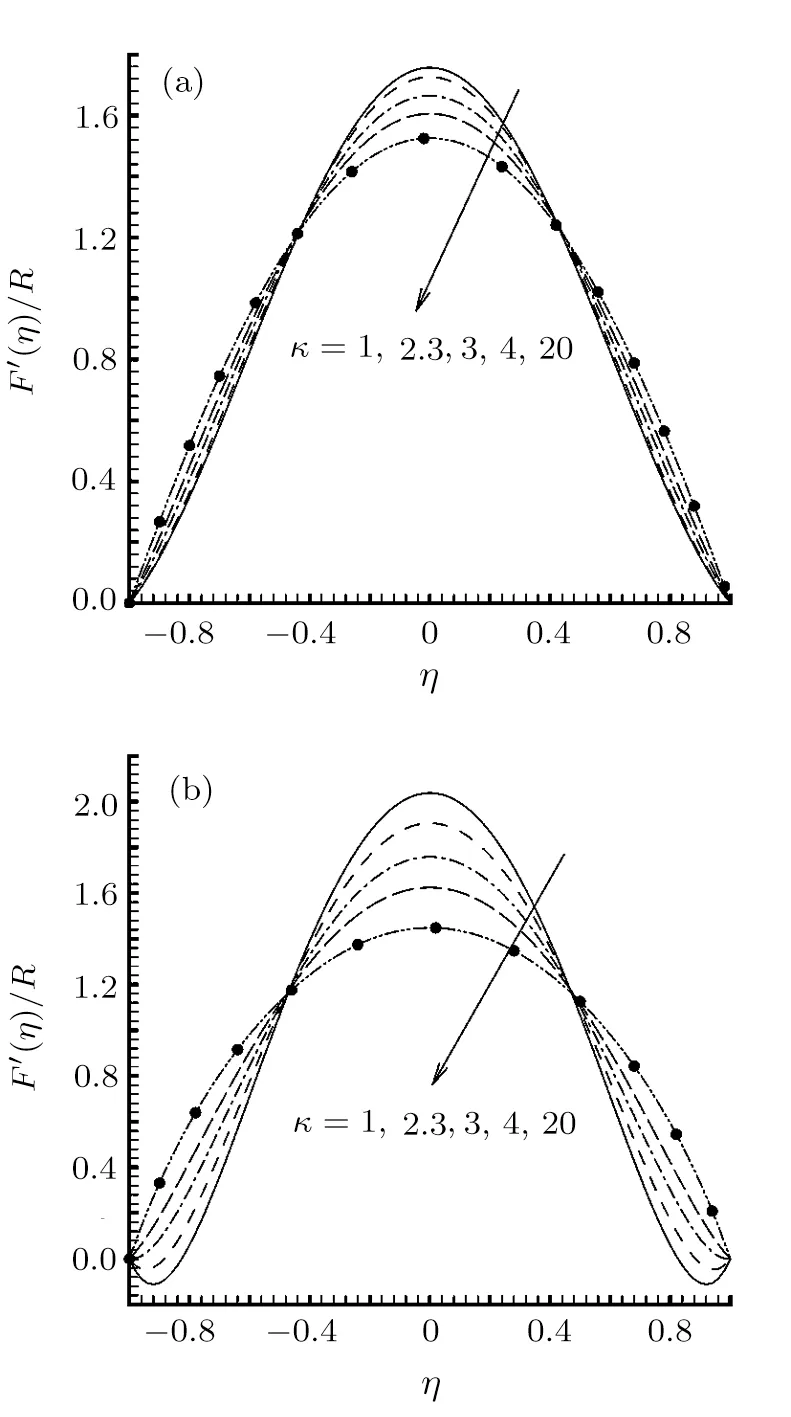
Fig.4 Distributions of the normalized velocity F′(η)/R for various values of κ at ζ=3 and G1=10.(a)R=5,(b)R=−5.
We then consider the effects of the physical parameters on important physical quantities.It is known from Eq.(27)that the volumetric rate of flow Q is only dependent on the Reynolds number R.While the ratio of the apparent viscosity to bulk viscosity µa/µ relies on K/R,the skin frictional coefficient Cfxis mainly determined by F′′(1)/R2,the stream potential Escan be computed via Eq.(36).To let the variational trends of those quantities illustrate more clearly,we normalize them by dividing them by their maximum values,i.e.where the values offor different cases are listed in Table 3,Tables 4 and 5 respectively.

Table 3 Maximum values of the reduced physical quantities for Fig.6.

Table 4 Maximum values of the reduced physical quantities for Fig.7.

Table 5 Maximum values of the reduced physical quantities for Fig.8.

Fig.5 Distributions of the normalized velocity F ′(η)/R for various values of G1at ζ=3 and κ =1.(a)R=5,(b)R=−5.
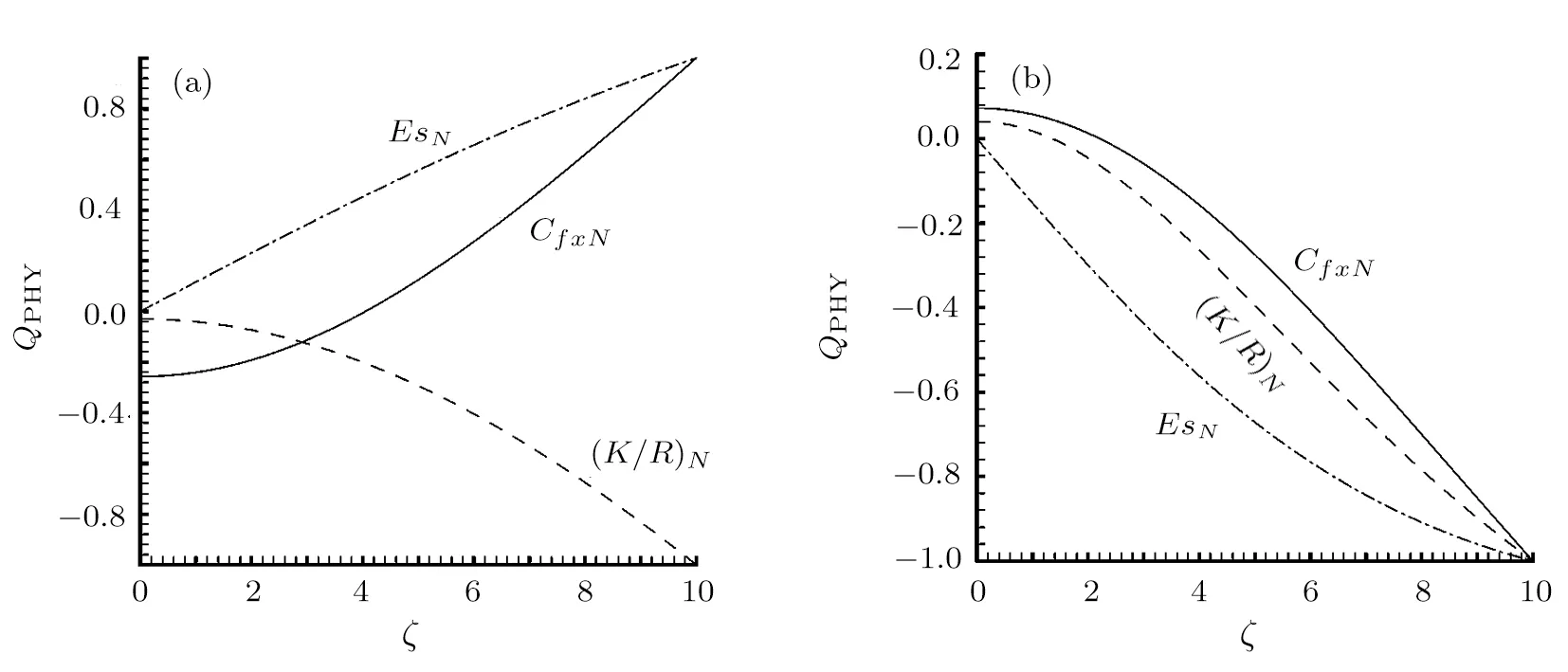
Fig.6 Various physical quantities vary with ζ at κ =1 and G1=10.(a)R=5,(b)R= −5.
It is seen from Fig.6 that,the increase of the zeta potential¯ζ causes the increment of the variational amplitudes of the reduced local skin friction CfxN,the stream potential EsN,and the reduction of the reduced ratio of the apparent viscosity to bulk viscosity(K/R)N.Physically,the increase of¯ζ indicates the enlargement of the electric body force,which accelerates of the fluid motion(the direction of fluid motion for positive R is opposite to that for negative R).As a result,the variational amplitude of the skin friction becomes large as¯ζ evolves owing to the increase of the velocity.Similarly,the changing amplitude for the pressure constant K enlarges with¯ζ growing.On the other hand,the stream potential is related to both the velocity and the electrical strength,so that its variational amplitude increases with¯ζ evolving.
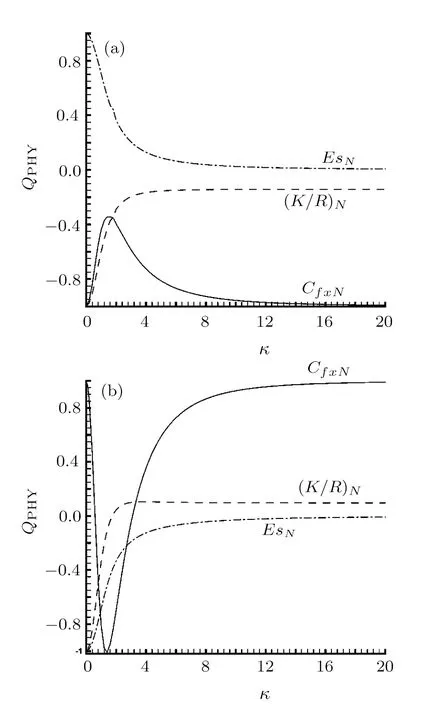
Fig.7 Various physical quantities vary with κ at=3 and G1=10.(a)R=5,(b)R=−5.
As shown in Fig.7,the variational amplitude of CfxNinitially decreases as κ grows,after reaching a peak value,it increases as κ continuously increases.Physically,for very small κ,the viscous force is dominant.As κ gradually increases,owing to the rapid reduction of the viscous force,the electrical body force starts to take action,but it is opposite to the skin friction force.As a result,the amplitude of CfxNreduces as κ increases.As κ is sufficiently large,the electrical body force becomes weak,again the viscus force gains the advantage.The changing amplitude of CfxNincreases as κ grows.While for(K/R)Nand EsN,both of their changing amplitudes reduce as κ increases.This is due to that the increase of κ indicates the increment of the electrokinetic separation distance,which results in the reduction of the electric strength in the channel.
Is is found in Fig.8 that increase of the coefficient of the streaming potential G1causes the increment of the absolute values of CfxNand(K/R)N,but leads to the decrease of the absolute value of EsN.Physically,the increase of G1means that the ratio of streaming current to conduction current increases,in other words,the fluid motion accelerates.This increment leads to the increase of the skin friction and the pressure,but results in the reduction of the streaming potential.

Fig.8 Various physical quantities vary with G1at=3 and κ =1.(a)R=5,(b)R= −5.
6 Conclusion
In this paper,a laminar microchannel flow between two paralleled flat plates with porous walls in the presence of the effects of the double layer electric field has been examined in detail.The linear model of the Poisson-Boltzmann type has been proposed to describe the double layer electric field in the vicinity of the solid-liquid interface.The equation of motion has been extended by considering the effect of the electrical body force generating from the double layer field.The fluid motion equation has been solved for the steady-state flow.The effects of various physical parameters such as the zeta potential,the electrokinetic separation distance,and the ratio of the streaming current to conduction current on the velocity,the pressure,the apparent viscosity of the fluid,as well as the streaming potential have been discussed.In summary,the main contributions of this paper are:
(i)The velocity profiles can be significantly affected by physical parameters such asκ,G1.Flow reversal could be happened if their effects become sufficiently large.
(ii) The physical quantities such as the local skin friction,the pressure,the apparent viscosity of the fluid,and the streaming potential can be altered remarkably by changingκ,G1.
(iii) Physical explanations on the changing trends of those physical quantities with various parameters are given.
 Communications in Theoretical Physics2018年10期
Communications in Theoretical Physics2018年10期
- Communications in Theoretical Physics的其它文章
- Topological Dark Matter from the Theory of Composite Electroweak Symmetry Breaking∗
- Analytical Investigation of Soliton Solutions to Three Quantum Zakharov-Kuznetsov Equations
- High Accuracy Split-Step Finite Difference Method for Schr¨odinger-KdV Equations∗
- Impact of Internal Heat Source on Mixed Convective Transverse Transport of Viscoplastic Material under Viscosity Variation
- Pair Production in Chromoelectric Field with Back Reaction∗
- Baryogenesis in f(R,T)Gravity∗
