Analytical Investigation of Soliton Solutions to Three Quantum Zakharov-Kuznetsov Equations

Rahmatullah Ibrahim Nuruddeen, Khalid Suliman Aboodh, and Khalid K.Ali

1Department of Mathematics,Federal University Dutse,Jigawa State,Nigeria

2Department of Mathematics,Faculty of Science&Technology,Omdurman Islamic University,Khartoum,Sudan

3Department of Mathematics,Faculty of Science&Arts,University of Bisha,Bisha,Saudi Arabia

4Mathematics Department,Faculty of Science,Al-Azhar University,Nasr-City,Cairo,Egypt

AbstractIn the present paper,the two-dimensional quantum Zakharov-Kuznetsov(QZK)equation,three-dimensional quantum Zakharov-Kuznetsov equation and the three-dimensional modified quantum Zakharov-Kuznetsov equation are analytically investigated for exact solutions using the modified extended tanh-expansion based method.A variety of new and important soliton solutions are obtained including the dark soliton solution,singular soliton solution,combined dark-singular soliton solution and many other trigonometric function solutions.The used method is implemented on the Mathematica software for the computations as well as the graphical illustrations.

Key words:two-dimensional QZK equation,three-dimensional QZK equations,soliton solutions

1 Introduction

Partial differential equations are of great importance in many physical phenomena describing particularly science and engineering models.However,one can easily find that the quantum Zakharov-Kuznetsov(QZK)equations[1−8]play vital roles in plasma physics that has to do with magnetized plasma and nonlinear ion-acoustic waves among others.[9]

The(2+1)-dimensional quantum Zakharov-Kuznetsov(QZK)equation is given by

the(3+1)-dimensional quantum Zakharov-Kuznetsov(QZK)equation reads

while the(3+1)-dimensional modified quantum Zakharov-Kuznetsov(MQZK)equation is

where p,q,r,and s are real-valued constants.Furthermore,since solution of a given problem helps in understating the physics and mathematics behind;different methods have been proposed to solve varieties of evolution equations.These methods include the Kudryashov method,[10−13]extended tanh based method,[14−18]rational expansion method,[19]Sine-Gordon and ansatz methods,[20−23]Jacobi elliptic function method[24]symmetry analysis method[25]and Adomian decomposition method[26−27]and other methods(see,Refs.[28–38])othors.

However,in the present article,we intend to analytically treat the above equations given in Eqs.(1)–(3)by constructing certain solitary wave solutions using the modified extended tanh-expansion method with the Riccati differential equation;[14−18]via the help of Mathematica software.The paper is organized as follows:Section 2 gives details about the methodology.Section 3 is for application of the method to the considered equations.In Sec.4 we give some graphical representations of the obtained solutions;and Sec.5 is for conclusion.

2 Analysis of the Method

We present the modified extended tanh expansion method by considering the nonlinear differential equation of the form:

where u=u(x,t).Also,we use the wave transformation

where a and d are nonzero constants.Substitution of transformation Eq.(5)into Eq.(4),we get a reduced ordinary differential equation of the form

where,′is a derivative with respect to ξ.Further,the solution is assumed to be of the finite series of the form:

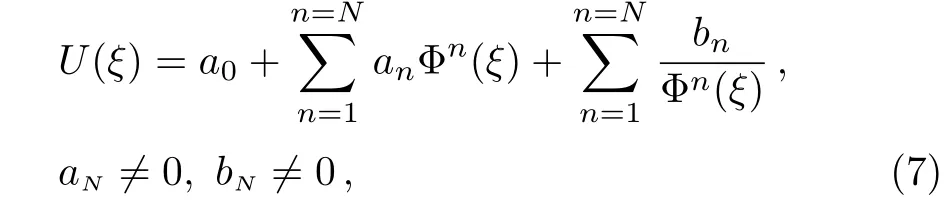
where a0,an,bn,n=1,2,...,N are nonzero constants and N is a positive integer determined by balancing the highest order derivative with the highest nonlinear term in the equation,and Φ(ξ)satisfies the Riccati differential equation:

where w is a constant.Further,the differential equation(8)admits the following solutions:

(i)if w=0,then

(ii)if w>0,then

(iii)if w<0,then

Substituting Eq.(8)and its necessary derivatives into Eq.(6)gives a polynomial in Φ(ξ)with P(Φ(ξ))=0.Collecting coefficients of the obtained polynomials and subsequently setting each one to zero,we will get a set of over-determined algebraic equations for a0,an,bn(n=1,2,...,N),and f with the aid of symbolic computation using Mathematica.Finally,solving the algebraic equations and the above possible solutions of differential equation into Eq.(7),we obtain the solution of Eq.(4).

3 Application

3.1 The(2+1)-Dimensional Quantum Zakharov-Kuznetsov Equation

We consider the(2+1)-dimensional quantum Zakharov-Kuznetsov(QZK)equation of the form

where u=u(x,y,t),p,q,and r are real-valued constants.Employing the wave transformation,

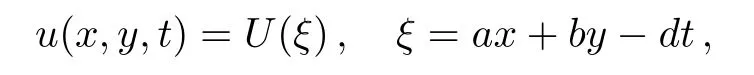
Eq.(9)becomes an ordinary differential equation:

integrating the above equation once with respect to ξ,get

and we assume the constant of integration zero.Now,balancing U2and U′by homogeneous balancing,we get N=2.Thus,Eq.(9)has a solution of the form to

where from Eq.(8)

Then,putting the values of Eq.(12)and its necessary derivatives together with Eq.(13)into Eq.(11);collecting all the coefficients of same powers of Φ(ξ)and thereafter setting them to zero,we get the algebraic equations below:

Solving the above system via Mathematica software,we get the following:

Case 1

Case 2

Case 3

Case 4

Case 5

Case 6

Thus,we get the following solutions for w>0:

Solution 1

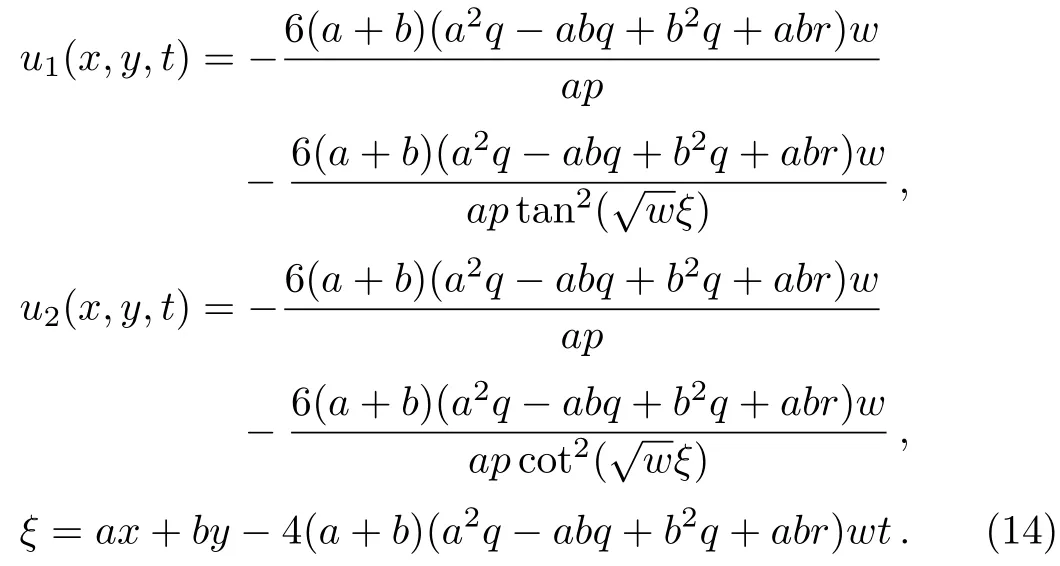
Solution 2

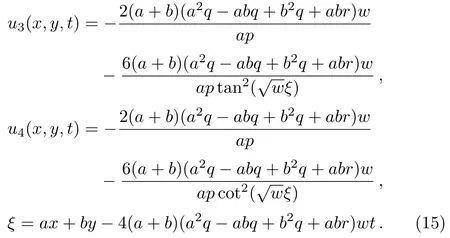
Solution 3

Solution 4

Similarly,for w<0 we get the following solutions:

Solution 5

Solution 6

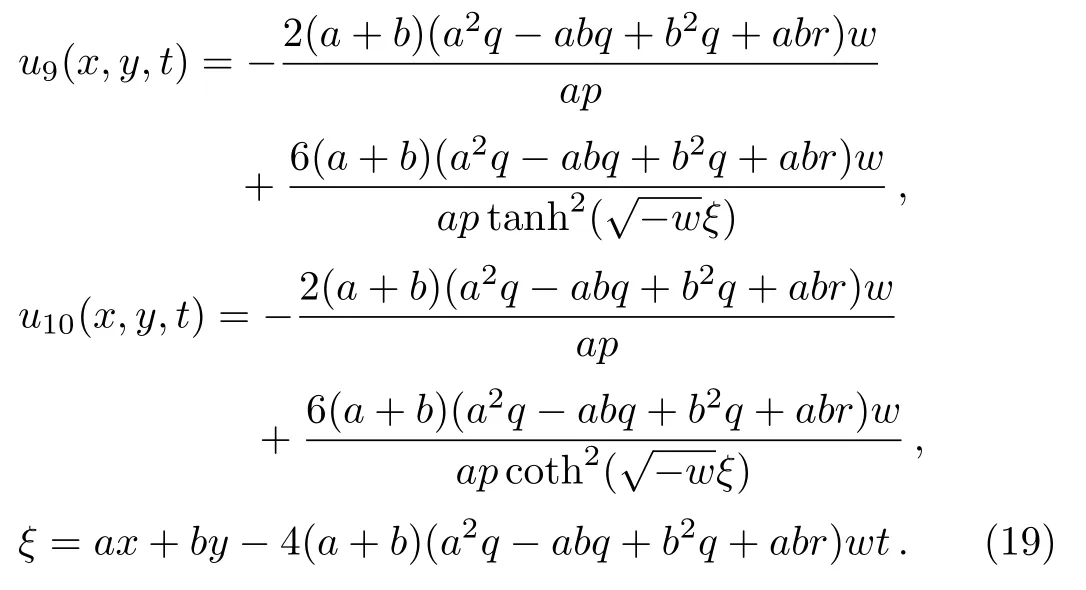
Solution 7

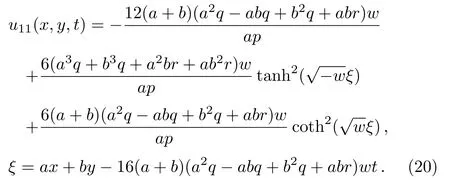
Solution 8

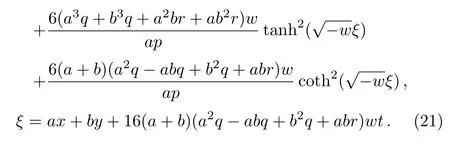
3.2 The(3+1)-Dimensional Quantum Zakharov-Kuznetsov Equation

We consider the(3+1)-dimensional quantum Zakharov-Kuznetsov(QZK)equation of the form

where p,q,r,and s are real-valued constants.Employing the wave transformation,

Eq.(22)becomes an ordinary differential equation:

integrating the above equation once with respect to ξ,get

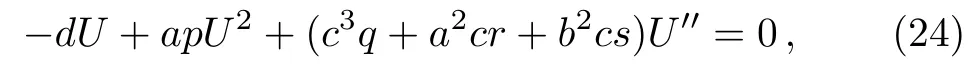
and we assume the constant of integration zero.Balancing U2and U′′by homogeneous balancing,we get N=2.Thus,Eq.(22)has a solution of the form to

where from Eq.(8)

So the young man stood carefully on one side, and by-and-bye he heard a great rushing in the water; and a horrible monster came up to the surface and looked out for the rock where the king s daughter was chained, for it was getting late and he was hungry

Then,putting Eq.(25)and its necessary derivatives together with Eq.(26)into Eq.(24);collecting all the coeffi cients of same powers of Φ(ξ)and thereafter setting them to zero,we get the algebraic equations below:

Solving the above system via Mathematica software,we get the following:

Case 7

Case 8

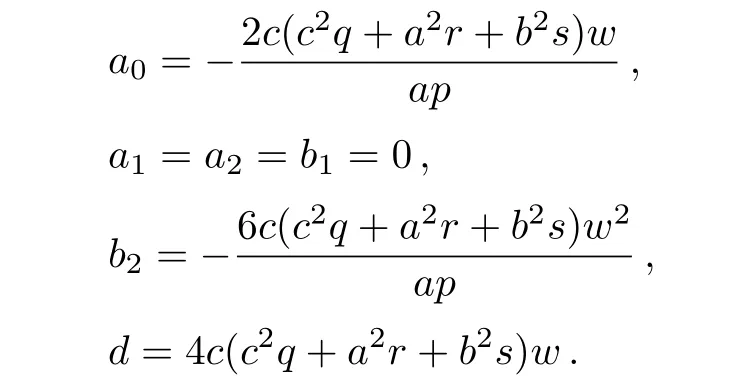
Case 9

Case 10

Case 11

Case 12

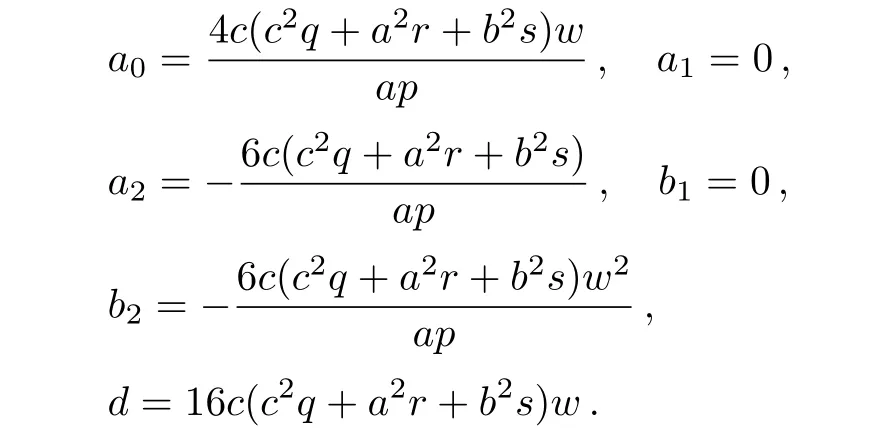
Solution 9

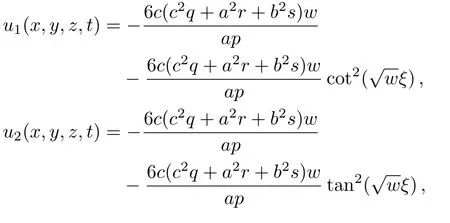
Solution 10

Solution 11

Solution 12

Also,we get the following solutions for w<0.

Solution 13

Solution 14

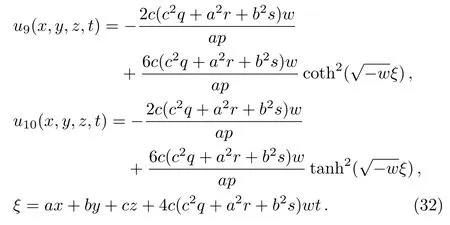
Solution 15

Solution 16

3.3 The(3+1)-Dimensional Modified Quantum Zakharov-Kuznetsov Equation

We consider the(3+1)-dimensional modified quantum Zakharov-Kuznetsov(QZK)equation of the form

where p,q,r,and s are real-valued constants.Employing the wave transformation

Eq.(35)becomes an ordinary differential equation:

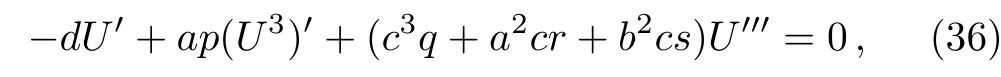
integrating the above equation once with respect to ξ,get

and we assume the constant of integration zero.Balancing U3and U′′in the above equation by homogeneous balancing,we get N=1.Thus,Eq.(37)has a solution of the form to

Then,putting Eq.(38)and its necessary derivatives together with Eq.(26)into Eq.(37);collecting all the coeffi cients of same powers of Φ(ξ)and thereafter setting them to zero,we get the algebraic equations below:

Solving the above system via Mathematica software,we get the following:

Case 13

Case 14

Therefore,we get the following solutions for w>0.

Solution 17

Solution 18

Also,we get the following solutions for w<0.

Solution 19

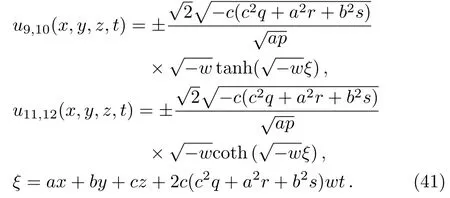
Solution 20

4 Graphical Representations of the Solutions

In this section,we give some 2-dimensional and 3-dimensional graphical representations of some solutions at different time levels.Figures 1–2 give the solitary plots for the(2+1)QZK equation in Eq.(9);Figures 3–4 give the solitary plots for the(3+1)QZK equation in Eq.(22)while Figs.5–6 give the solitary plots for the(3+1)modified QZK equation in Eq.(35).

Fig.1 Exact solutions for the(2+1)QZK equation in Eq.(9)at t=10.

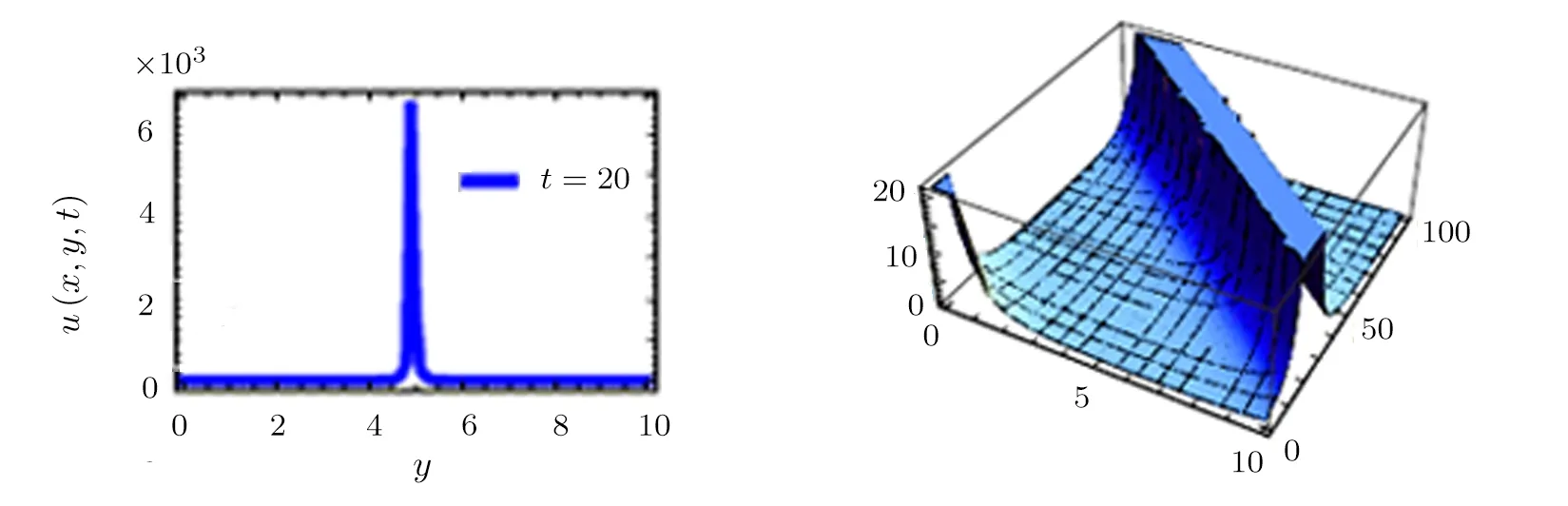
Fig.2 Exact solutions for the(2+1)QZK equation in Eq.(9)at t=20.

Fig.3 Exact solutions for the(3+1)QZK equation in Eq.(22)at t=10.

Fig.4 Exact solutions for the(3+1)QZK equation in Eq.(22)at t=20.

Fig.5 Exact solutions for the(3+1)modified QZK equation in Eq.(35)at t=10.

Fig.6 Exact solutions for the(3+1)modified QZK equation in Eq.(35)at t=20.

5 Conclusion

In conclusion,we have engaged the modified extended tanh-expansion method toconstructvarious exact soliton solutions for the two-dimensional quantum Zakharov-Kuznetsovequation,three-dimensional quantum Zakharov-Kuznetsovequations,and threedimensionalmodified quantum Zakharov-Kuznetsov equation. Various trigonometric and hyperbolic function solutions including the dark soliton solution,singular soliton solution,combined dark-singular soliton solution,and many others were obtained by the method and validated using the Mathematica software.These new soliton solutions obtained will help greatly in studying the physical aspects of the considered problems.Thus,the used method is promising and can be applied to several problems in this regards.