基于Matlab平台的图论模型的仿真实验

孙建英

(青岛理工大学 琴岛学院， 山东 青岛 266106 )

图论模型是数学建模中一类非常重要的模型，它的应用非常广泛。购买机票、设备更新、配送路线选择等，都属于最短路径问题；景区的旅游车辆的最大通行量、石油管道的最大输送量等，都属于最大流问题；电线的架设问题、居民区的供水管道问题等，都属于最小支撑树问题。Matlab2014a平台中的图论工具箱，可以实现图论模型的快速求解，不必编写复杂的程序，对计算机不是很懂的学者也可以很快地掌握。本文从3个实例出发，详细介绍了如何利用图论工具箱快速准确地求解图论模型中的最短路、最大流和最小支撑树问题，对图论模型的进一步研究有重要意义和实用价值。

1 预备知识

1.1 图论工具箱

Matlab2014a平台下图论工具箱中的相关函数，如表1所示。

表1 Matlab 图论工具箱中的相关函数

1.2 稀疏矩阵

稀疏矩阵是指零元素很多，非零元素比较少的矩阵。

稀疏矩阵的存储方式：a(i,j)=m，其中，a表示稀疏矩阵，i表示非零元素的行标，j表示非零元素的列标，m表示非零元素的数值。

稀疏矩阵的使用说明：1)有向图中，可以直接使用Matlab中的sparse命令,把邻接矩阵转化为稀疏矩阵；2)无向图中，由于Matlab只存储下三角矩阵中的非零元素，要先把邻接矩阵转置，再应用sparse命令。

2 实例仿真

2.1 最短路问题

例1购买机票问题[1]：某集团公司在六个城市C1,C2,…,C6中有分公司，从Ci到Cj的直飞航程票价如表2所示(“-”表示无直飞航班)。如今，集团巡视组要分别从C1出发到其他城市去检查工作。请问：应该如何安排航班，方可使得票价最低？

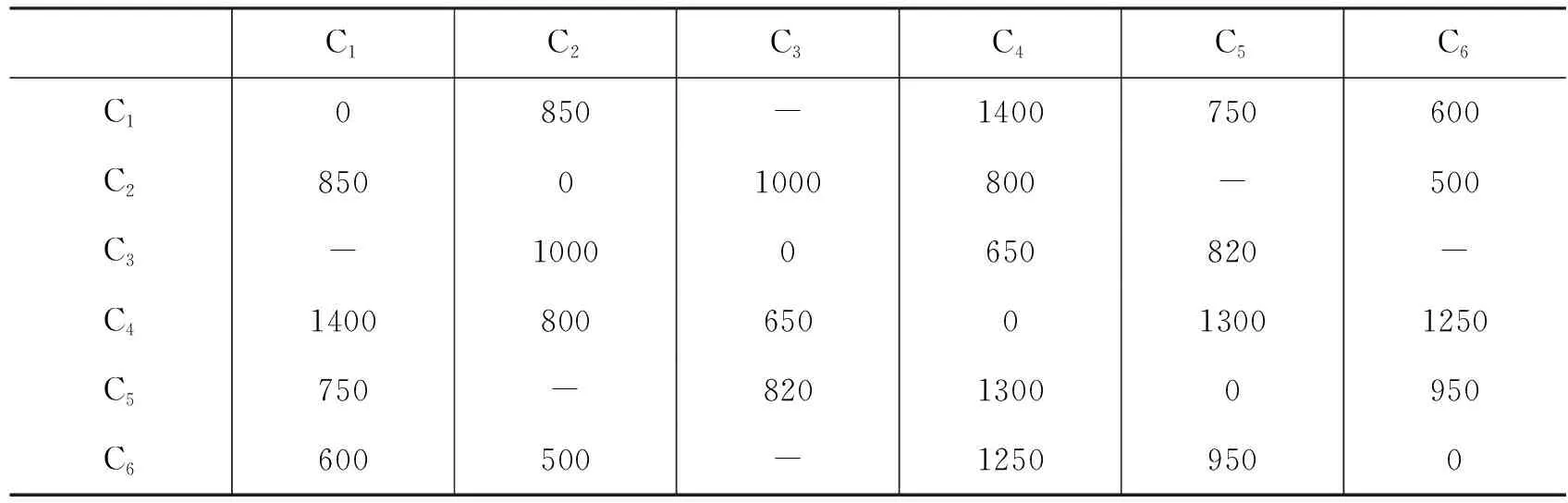
表2 各分公司所在城市之间的航程票价(单位：元)

解：Matlab程序：

clc,clear

a=zeros(6);

a(1,2)=850;a(1,4)=1400;a(1,5)=750;a(1,6)=600;

a(2,3)=1000;a(2,4)=800;a(2,6)=500;

a(3,4)=650;a(3,5)=820;

a(4,5)=1300;a(4,6)=1250;

a(5,6)=950;

a=a’;

a=sparse(a);

b=[1:6];

[price,path]=graphshortestpath(a,1,b,’Directed’,0)

运行结果：

price=

0 850 1570 1400 750 600

点击工作区中的path，出现path变量表，见表3。

表3 path变量

结果分析：C1直达到C2，C4，C5，C6，票价分别为850，1400，750，600；C1经C5

转机到C3，票价为750+820=1570。

2.2 最大流问题

例2管道输流问题[1]： 某石油公司拥有一个管道输送网络系统，如图1所示，使用该系统将石油从开采地A输送到销售地G。由于管道(以两个地点之间的弧表示)直径的变化，各段管道的容量是不一样的，弧上的数字意味着各管道的最大容量(单位：万加仑/小时)。请问：欲使得从开采地A到销售地G每小时输送的石油量最大，应采取什么样的配送方案？最大配送量是多少万加仑？

解：Matlab程序：

clc,clear

a=zeros(7);

a(1,2)=6;a(1,3)=8;a(2,4)=3;a(2,5)=6;

a(3,4)=4;a(3,6)=1;a(3,7)=3;

a(4,5)=3;

a(5,7)=5;a(6,7)=4;

b=sparse(a);

[Maxflow,path]=graphmaxflow(b,1,7);

Path=sparse(path);

Maxflow

view(biograph(Path,[],’ShowArrows’,’on’,’ShowWeights’,’on’))

运行结果：

Maxflow=9

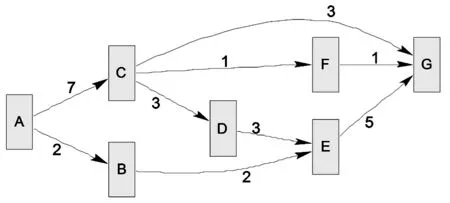
图1 石油输送量最大的配送方案

2.3 最小支撑树问题

例3电线架设问题[2]：如图2，S、A、B、C、D、E、T代表村镇，它们间连线表明各村镇间现有道路交通情况，连线旁数字代表道路的长度。现要求沿途中道路架设电线，使上述村镇全部通上电，应如何架设使总的线路长度为最短？

解：Matlab程序：

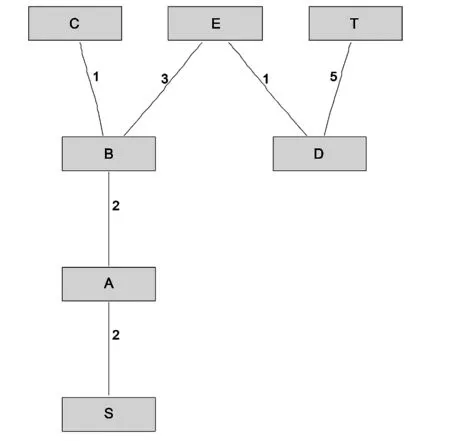
图2 线路最短的电线架设方案

clc,clear

a=zeros(7);

a(1,2)=2;a(1,3)=5;a(1,4)=4;

a(2,3)=2;a(2,5)=7;

a(3,4)=1;a(3,5)=5;a(3,6)=3;

a(4,6)=4;

a(5,6)=1;a(5,7)=5;

a(6,7)=7;

a=a’;

a=sparse(a);

[ST,pred]=graphminspantree(a,’Method’,’Kruskal’);

st=full(ST);

treelength=sum(sum(st))

view(biograph(st,[],’ShowArrows’,’off’,’ShowWeights’,’on’))

运行结果：

treelength=14

3 结语

图论中的最短路、最大流和最小支撑树问题，在Matlab2014a平台下，可以利用图论工具箱快速地得到最优解。其实，运筹学中的很多模型，像整数线性规划和目标规划问题[3]等，也可以借助Matlab实现快速求解。但是还有很多问题，例如有初始可行流的最大流问题和最小费用最大流问题等，目前，Matlab没有相应的函数可以直接求解，要转化成线性规划模型，再利用Matlab或者lingo软件求解[4]。Matlab软件已成为解决图论问题的强有力的工具，可以帮助科研工作者及时、准确地作出决策。