GPRs搭接网络分解优化定理在流水作业中的应用

孔 峰，张 睿，吴 甜

(华北电力大学经济与管理学院，河北 保定 071003)

1 引言

GPRs(Generalized Precedence Relations)搭接网络计划技术是在经典的CPM网络计划技术基础上的发展[1]，由Crandall[1]在1973年提出后广泛吸引了各国学者和应用者的注意。在GPRs网络计划中相邻工序之间的时间约束(搭接)关系，不仅存在传统的FTS(Finish To Start)型的，还存在FTF(Finish To Finish)、STS(Start To Start)、STF(Start To Finish)型时间约束。这种带有多种时间约束关系的网络计划更贴合工程实际，尤其在工期长、工序多、工艺复杂的大型工程项目中具有广阔的应用前景。

当前，关于GPRs网络计划悖论和最短工期研究也日益广泛。Elmaghraby和Kamburowski[2]对GPRs网络的基本概念做出了系统地阐述，奠定了GPRs网络的理论基础，并发现其中存在逆向关键工序引起的总工期悖论。刘树良等[3]提出搭接网络中存在某些关键工序在压缩量较大时，总工期不但缩短反而延长，以及压缩或延误关键工序总工期均不变的奇异现象等等。阚芝南等[4]发现双代号搭接网络中存在“工序间加入不同表现形式的同一时间约束，可能会产生不同的最大路长”这个悖论，并提出双代号搭接网络的一种新表示方法和求解搭接网络次关键路线的一系列精确算法。苏志雄等[5]设计了新的表示方法，即将工序之间所有的搭接关系都等效的利用传统的CPM法表示，在新的表示方法中发现了某些关键工序的缩短，总工期反而延长，而某些非关键工序无论如何变动，其总时差总保持不变等现象。这些研究为项目计划优化问题提出了新的挑战，开拓了GPRs搭接网络在研究和应用上的新领域。

国内学者将重复性项目调度称为“流水施工”或“流水作业”[6]，基于GPRs网络的重复性建设项目工期计划的研究具有重大的实际意义。关键路线的长度决定项目总工期，研究认为流水作业中施工段的划分对关键线路的长度有重要影响，科学合理的划分施工段会大大缩短关键线路长度。其中具有代表性的研究有：Selinger[7]最早提出了重复性项目中的最短工期问题，其假定所有工序均存在多种可选择执行模式，并在保持工作连续性要求和资源恒定性要求条件下给出了该问题的动态规划求解模型。Harris和Ioannou[8]在重复性工程项目进度计划管理中也引入了GPRs网络，发现总工期悖论也会出现。重复性建设项目需要合理计划，以确保资源的不间断使用，Harris和Ioannou[8]认为传统关键路径法不能满足此要求，提出采用重复调度方法(RSM)以保证施工计划中的资源连续性。Alexandros等[9]比较了Kallantzis -Lambropoulos的关键路径重复项目模型与网络计划关键路径法，指出了两者之间的异同。杨冰[10-11]把网络计划、搭接网络计划和流水网络计划统一起来，计算模型更为严谨、简明、便于应用。蒋根谋[12]等称流水作业计划为线性计划方法，并介绍了线性进度计划的绘制方法和步骤。张立辉等[13]提出了借助约束线确定重复性项目中关键路线的方法。总之基于GPRs网络的工期优化方法已经成为流水作业研究的主流方向之一。

通过对GPRs网络的总工期悖论研究，本文首次发现了在GPRs搭接网络中还存在“分解悖论”，即编制网络计划时，将某一个可分解的关键工序分解成两个顺序工序(FTS=0)以后，总工期并非保持不变反而缩短的奇异现象，工序的分解也使工序获得更多可利用的总时差。通过对该分解悖论的研究，本文提出了两个分解优化定理，用于GPRs搭接网络计划的优化。这种优化方法不仅解决了GPRs搭接网络中正确求解最短总工期的问题，还发现在总工期不变的条件下，分解某一非关键工序会增加其总时差。总时差的增加为资源优化创造了条件。工序的合理分解(施工段的科学划分)正是流水作业的重要内容之一，本文将该分解优化方法同流水作业原理相结合，用于解决流水作业中施工段划分的问题，并通过实例验证了该方法的可操作性。这对大型重复性项目的建设有着重要的实践指导意义。

2 GPRs搭接网络的关键工序分解悖论

在实际施工过程中，大部分工序因为技术间歇、人员调度、机械设备调度、工作时间限制等各种各样的原因，可以进行合理分解，尤其是对于大型重复性项目。传统CPM理论认为关键工序被分解成若干具有FTS=0的工序，总工期和时间参数均不会发生改变；在某工序中插入一段休息时间会使项目的总工期变长。但本文研究发现对特定工序进行分解，反而使总工期减少，工序的机动时间也得到增加。这种不需要增加资源投入量的工序分解方式，不但满足工期优化的目标，还节省了大量的资金成本。

本文以如图1所示的网络图为例进行分析。

图1 GPRs搭接网络计划图初始方案

2.1 分解悖论现象

在搭接网络计划中，工序间的约束关系是由相邻两工作之间的施工速度决定的。如果前一工序施工速度较后一工序快，则采用“STS”型；如果前一工序施工速度比后一工序慢，则采用“FTF”型。图1的搭接网络中各个字母表示不同工序，其中St表示开始工序，Fin表示结束工序，仅表示逻辑关系不具有实际意义。

图1网络图中关键线路为St→A→E→F→ H→Fin,总工期为46，工序A、E、F、H为关键工序。将工序E分解为E1和E2两个具有FTS=0的顺序工序，工序持续时间分别为3和4，重新绘制和计算网络图，结果如图2所示。

根据图2的计算结果可以看出，工序分解后关键线路发生了变化，为St→C→D→G→Fin,而且E1和E2都不再是关键工序，总工期也缩短为41。显然，当关键工序E可以分解时，分解之后的网络图优于初始网络图。

分解悖论还可以用另一种表现形式——咖啡时间悖论来说明。

在初始网络图中的关键工序E中插入1个咖啡时间(休息时间)E0，即在拆分后的工序E1和E2中，插入一个持续时间很短的工序E0，则E1、E0和E2成为三个搭接关系为FTS=0的顺序工序，持续时间分别为3、1、4，重新计算网络图后结果如图3所示。

图2 关键工序分解悖论

图3 咖啡时间悖论

相比于初始网络图，增加工序后总工期反而减少为41天，关键线路变为St→C→D→G→Fin。这种在某一可分解关键工序中插入休息时间(咖啡时间)后，工序虽然增加了，但是总工期却缩短的现象称为咖啡时间悖论。图3的原理与图2相同。

2.2 悖论原因分析

(1)关于关键工序分解悖论的分析

将某关键工序进行合理分解，总工期缩短的原因在于：由于工序A、E之间为STF的搭接关系，即工序A只对E的结束有直接约束，分解后该约束变为A与E2之间，工序E2需要在工序A开始后20内结束。工序E1与工序A没有直接约束关系。因此，项目开始后E1即可开始，E1最早开始时间提前了13。又由于工序E1和F之间为STS搭接关系，这就使得工序F的最早开始时间也提前了13，其所在线路长度缩短，使得关键线路发生变化，总工期缩短。

(2)关于咖啡时间悖论的分析

咖啡时间悖论和分解悖论产生的原因相似，插入咖啡时间后工序A仅对工序E2有STF的搭接关系，工序E1与工序A并不存在直接约束，所以E1工序的最早开始时间也提前，由于工序E1和F之间为STS搭接关系，这就使得工序F的最早开始时间也提前了，线路长度缩短，导致关键线路发生变化，总工期缩短。

2.3 关键工序分解优化定理

分解悖论(包括咖啡时间悖论)的存在，说明在项目没有增加资源投入的情况下，甚至增加休息时间，总工期却缩短。也就是说，原有网络计划中存在帕累托改进。因此，需要进行更科学的优化，在不增加资源投入的条件下，确保实现最优(最短)总工期。GPRs网络中存在如下的关键工序分解优化定理。

分解优化定理1：

若某一网络图中所有的关键线路，均存在如下情况，网络的总工期是可以得到优化的。

(1)某些关键工序是可以进行分解的；

(2)该关键工序与其紧前关键工序之间存在STF或FTF的搭接关系，且该关键工序与其紧后关键工序之间存在STS或STF的搭接关系。

证明：

只需证明其中1条关键路线的长度可以缩短，其它关键线路同理即可。

(1)在某关键路线中，某关键工序j与其紧前工序i之间存在STF的搭接关系，与其紧后工序k存在STS的搭接关系(简称STF-STS组合)。ESk为工序k的最早开始时间，STSj-k表示工序j与k之间存在STS的搭接关系，其他类似。

分解前，有，ESk=ESj+STSj-k

由于工序j为关键工序，其最早完成时间由与其具有STF搭接关系的紧前关键工序i决定，因此有，

ESj=max(EFj-tj,其它约束)=EFj-tj

即有，EFj-tj>其它约束。

由于工序j1与工序i之间没有了约束，其最早时间由其它约束决定，即，ESj1=max(其它约束)

所以有，ESj>ESj1。

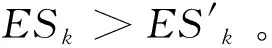
所以经过工序k的关键线路变短。

(2)其它三种情况类似，即STF-STF组合、FTF-STS组合、FTF-STF组合证明同上，略。

证毕。

3 总时差悖论及搭接网络分解优化方法

3.1 总时差悖论现象

分解悖论不仅仅体现在关键工序和总工期的改变上，进一步分析，经观察可发现，图3中插入“咖啡时间”E0后，E0总时差为21，证明其有充分的可利用机动时间(总时差)，而且工序E1同E2的总时差并未改变，仍与图2中相同，分别为8和9。

相比于图1中没有总时差的工序E，其可利用的机动时间(总时差)增加了许多。工序总时差的增加，使得项目有更多可利用的机动时间，资源优化空间大幅提升。

工序分解后总时差增加的原因分析：

(1)插入E0前：由于图2中工序E1和工序F之间STS搭接关系的存在，工序E1的最迟开始时间为LSE1=min(28-20，25-3)=8，是由STS搭接关系决定的。因此，无论E1持续时间如何变化，其总时差为定值8。

而工序A与E2之间STF搭接关系确定了E2的最早完成时间，为固定值20。同时，关键线路已确定总工期，所以工序E2的最迟完成时间为29始终不变。因此，工序E2的总时差为定值9。

(2)插入E0后：插入咖啡时间E0后，由于LSE0=min(28-20，24-3)=10，所以E1总时差保持不变为8。且工序E2的总时差仍为定值9天，工序E0具有总时差21，所以插入E0后总时差增加。

该特性不仅存在于非关键工序上，同样也会出现在关键工序中。将图3中的关键工序D拆分为D1和D2两个具有FTS=0搭接关系的顺序工序，持续时间分别为10和3，重新绘制并计算网络图，如图4所示。

由图中计算结果可知，工序D1总时差为8。

图3和图4的计算结果证明了有的工序在分解后不仅不会改变总工期，反而为工序自身获得了更多的总时差。进一步说明合理的分解工序可以达到项目的优化。

3.2 总时差分解优化定理

GPRs中存在如下关于总时差的分解优化定理。

分解优化定理2：

在GPRs网络中，若存在以下情况，通过工序的分解可以得到更多的总时差，即总时差的分布得到优化。

(1)某工序是可以进行分解的；

图4 分解悖论拓展分析——总时差悖论

(2)该工序与其紧前工序之间存在STF或FTF的搭接关系，且该搭接关系是起决定作用的约束；或该工序与其紧后工序之间存在STS或STF的搭接关系，且该搭接关系是起决定作用的约束。

证明：

(1)假设在网络图中，某工序i与其紧后工序j之间存在STF的搭接关系，且该搭接关系是起决定作用的约束。

则工序i的最迟完成时间：

LFi=min(EFj-STFij+ti,其它约束)=EFj-STFij+ti

即有，EFj-STFij+tB<其它约束。

工序i分解为工序i1和工序i2后，工序i2的最迟完成时间：

LFi2=min(其它约束)

因此，有，LFi2>LFi。

由于，LFi=LFi-EFi,LFi2=LFi2-EFi2

又因为，

EFi2=ESi2+ti2=EFi1+ti2=ESi1+ti1+ti2

=ESi1+ti=ESi+ti=EFi

因此，TFi2>TFi。

又因为，LSi1=LSi,ESi1=ESi，

因此，TFi1=TFi。

工序i分解后的工序i1的总时差与分解前相同，而工序i2总时差大于i的总时差，说明工序i分解后总时差增加。

(2)其它情况类似，证明略。

证毕。

可以看出，上述两个分解优化定理本质是相同的，都是通过工序的分解得出工序的最大总时差。可分解的工序与其紧前或紧后工序之间存在搭接关系，约束了其开始或结束时间，通过合理的工序分解使得被约束对象趋于合理。定理1可以得到正确的关键工序，定理2可以得到最大的总时差。

3.3 搭接网络的分解优化方法

根据前面两个分解优化定理，得到GPRs网络的分解优化方法：

若某工序可以进行分解，且存在下述起决定作用的搭接关系时，可以按照以下方法进行分解优化：

(1)某工序与其紧前工序若存在STF或FTF的搭接关系，则该工序应该分解为两个具有搭接关系FTS=0的工序，其中后者为不能继续分解的基本工序。

(2)某工序与其紧后工序若存在STS或STF的搭接关系，则该工序应该分解为两个具有搭接关系FTS=0的工序，其中前者为不能继续分解的基本工序。

因此，对于图1网络，最终的优化结果如图5所示。其中，工序A1、E0、E2、D2为不能分解的基本工序。

相比于图1 中的初始方案，图5的方案总工期得到了减少，部分工序的机动时间也大大增加，有的工序还具备了休息缓冲的时间。可见，分解优化定理对于项目优化管理有重要意义。

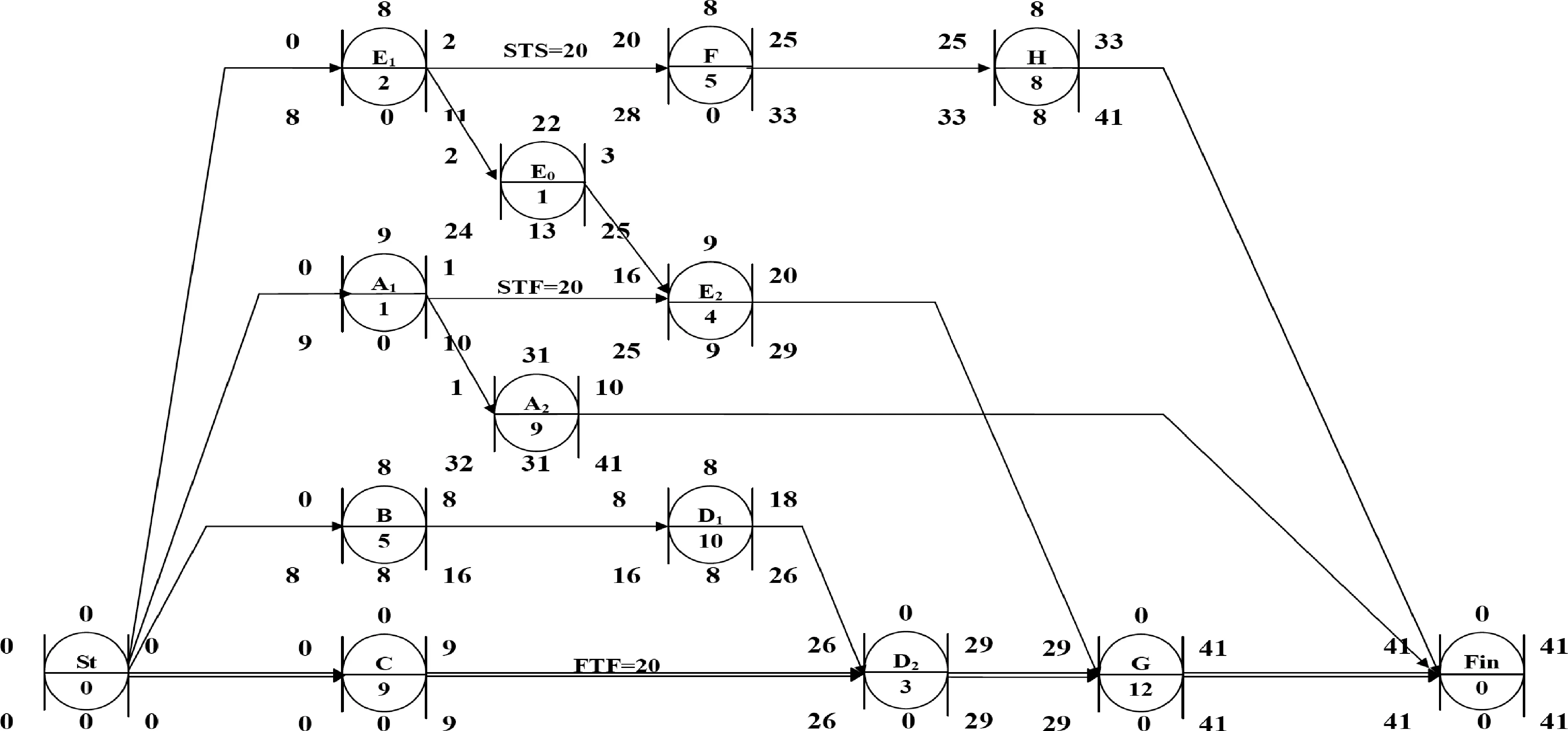
图5 GPRs搭接网络图最终优化方案

4 分解优化定理在流水作业网络计划中的应用

流水施工需将拟建工程的全部建造过程根据工艺和工程量分解为若干个施工过程，竖向的划分称之为施工层，平面上的划分称之为施工段。各组专业工人则根据施工对象的需要划分成若干个专业小组或混合专业小组，将其按照施工顺序安排在工作性质相同施工段上，依次投入施工。流水作业作为一种先进的作业方式得到了广泛的应用。

施工段的划分是流水作业施工中最主要的内容之一，将分解优化定理科学合理的应用于流水作业原理中，即通过合理的施工段划分(工序分解)，会有效的缩短总工期，使得工程项目建设更加高效合理。

本文以下一算例进行分析。

某一高架桥工程，该高架桥全长1189米，基本施工工序包括基础施工、桥台施工、桥台后填土、预制梁的架设、桥面附属工程和同两侧道路路基的连接。具体施工工序及各工序持续时间如表1所示。为保证工程的早日完工，该工程采用流水作业施工，将基础、桥台工程均分为东、西两个施工段。为尽早通车，加之山沟的地势条件，该高架桥西侧基础与西侧桥台施工之间存在STS=15天的搭接关系，东侧基础同东侧桥台施工之间存在FTF=20天的搭接关系。此外，架梁时不仅需满足桥梁自身的使用要求，也要保证同两侧公路路基对接良好，故架梁工序同桥面系及附属工程之间存在STF=20天的搭接关系，STSC-D表示工序C与D之间存在开始到开始的搭接关系。

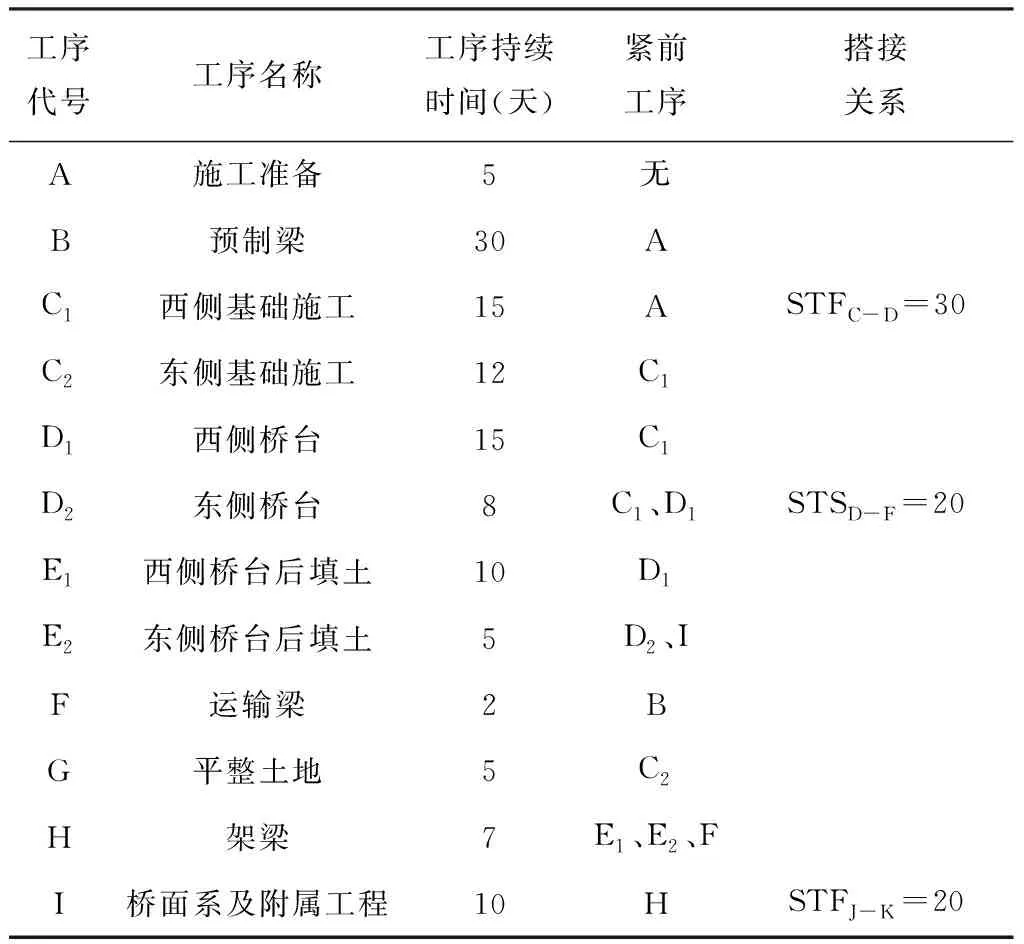
表1 高架桥施工工序及施工时间一览表

初始施工方案的流水作业网络计划图及各个工序的参数计算结果如下图6所示。

由图可知，该高架桥工程总工期为76天，其中关键线路为St→A→C1→C2→D2→E2→H→ I→Fin。关键工序C2和其紧前工序C1之间存在STF的搭接关系，与其紧后工序D2之间存在STS的搭接关系，根据关键工序分解优化定理可将工序C2进行分解。结合本实例，分解工序C2实际上就是将基础施工的施工段重新划分，可将工序C2拆分为两个具有FTS=0的顺序工序，即将东侧基础施工划分为两个施工段，则基础部分被划分为C1、C2、C3共三个施工段。显然，工序H也具备可分解的条件，故可将工序H划分为两个具有FTS=0的顺序工序H1和H2。分解优化后的流水作业网络图如图7所示。

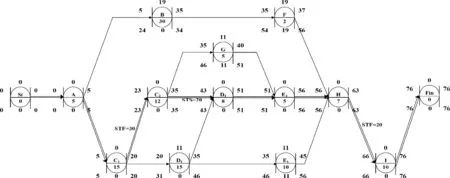
图6 高架桥流水施工初始方案GPRs网络图

图7 高架桥分解优化施工方案GPRs网络图

优化后该高架桥项目施工总工期缩短为68天，关键线路为St→A→C1→D1→D2→E2→H1→ I→Fin。施工段重新划分之后，工序D1和D2的总时差分别增加为11天和4天，工序J2的总时差增加为13天，工序F的总时差增加为1天。由此可见，分解优化定理具有很强的应用性。对于一些应用流水作业原理施工的大型重复性建设项目，分解优化定理对其施工段的划分具有重要意义。

5 结语

本文发现了传统GPRs搭接网络计划方法中的一些新的奇异现象，如在某一可分解关键工序中加入一休息时间或分解关键工序，总工期反而缩短，这些奇异现象分别称为咖啡时间悖论和关键工序分解悖论。通过对这些悖论形成原因进行分析发现，在没有增加任何资源的情况下，甚至增加了休息时间，总工期反而缩短。说明传统GPRs搭接网络计划的总工期计算结果在某些情况下存在帕累托优化改进，需要进行更科学的优化，对此，本文提出了关键工序的分解优化定理。在对工序分解进行拓展分析过程中总结并又提出了总时差分解优化定理，通过对工序的合理分解来最大程度上优化工序的总时差分布，并通过算例表明这些方法的有效性和简便性。总时差分解优化定理说明了GPRs网络计划中的分解优化不仅仅适用于关键工序，对某些非关键工序也同样适用。本文还将分解优化定理同流水作业原理相结合，通过实例说明了分解优化原理在流水作业施工段分解方面的实际可操作性，为项目资源优化提供了更科学的理论依据，从而有利于项目的资源优化和降低成本。