考虑社交网络用户行为的网络病毒传播建模

冯丽萍,韩 燮,韩 琦,郑 芳

(1.中北大学 信息与通信工程学院,太原 030051; 2.山西财经大学 信息管理学院, 太原 030006; 3.忻州师范学院 计算机系,忻州 034000; 4.重庆科技学院 电气与信息工程学院,重庆 401331)(*通信作者电子邮箱fenglp@yeah.net)

0 引言

在信息化建设高度发达的今天,互联网应用已经渗透到各个领域,给人们的生活和工作带来了极大的方便。然而,网络服务给人们带来方便的同时,网络安全已成为一个非常严重的全球化问题。2010年6月爆发的震网病毒(Stuxnet),是一次极具破坏性的、针对现实世界基础设施的蠕虫病毒,在短时间内感染了全球超过45 000个网络,伊朗核电站因此受到严重损失[1]。2017年5月12日爆发的勒索病毒(WannaCry)感染了全球100多个国家和地区,超过10万台电脑,涉及到金融、能源、教育以及医疗等多个行业[2]。可见,建设安全、可靠的网络空间环境是推动信息化社会不断发展的基本保障。

社交网络作为眼下最具影响力的网络社交平台,已拥有大量用户。以我国最流行的微信、QQ为例,2016年,网民使用率分别达到 85.8%、67.5%[3]。这些用户,以自己在现实世界中的关系网为基础,建立联系人列表、微信群或QQ群。这些用户之间存在着错综复杂的关系,很容易引起交互感染。比如,用户A的联系人列表里有用户B,但是A和B所处的微信或QQ群不一定完全一样,假如用户A受到了感染,那么A就会感染B,从而产生了不同用户群之间的相互感染。本文的目的旨在研究不同社交网络间用户相互感染的网络病毒传播动力学行为。

针对网络病毒传播建模和用户行为的研究已有许多,自从1991年Kephart等[4-5]将人类病毒传播建模机理引入计算机病毒传播研究,许多学者在此基础上做了大量网络病毒建模的工作。Zou等[6]通过建立SIR(Susceptible-Infected-Recovered)模型,分析了“红色蠕虫”传播的动力学特性,并且通过与实际红色蠕虫传播数据比较,表明微分方程动力学模型可以有效地反映真实网络病毒传播规律。Han等[7]建立了带时滞的SIRS(SIR-Susceptible)模型,刻画了具有延迟感染的计算机病毒传播过程,通过详细的数学分析,得出了控制计算机病毒大规模扩散的阈值,最后,通过数值仿真验证了理论分析的正确性。冯丽萍等[8]考虑到现实网络中节点数量是可变的,在已有工作基础上建立了改进的SIR模型,并且分析了模型的动力学性态,通过与2001年红色蠕虫爆发时实际观察值的比较发现,根据模型得到的仿真结果和实际观察值基本相符。紧接着,冯丽萍等[9-11]又通过考虑网络病毒扩散依赖的不同因素,建立了一系列不同的病毒传播模型,进一步研究了网络病毒传播的动力学性质,以及控制病毒扩散的有效措施。还有许多研究者做了大量类似的工作[12-15]。这些已有的研究从不同侧重点揭示了网络病毒传播规律,为网络管理员采取合理的网络安全防御措施提供了良好的理论指导,而且这些模型从不同角度考虑了用户的反病毒行为对网络病毒传播速度以及规模的影响。但是,针对不同社交网络间用户行为的相互作用而引起的网络病毒传播规律还没有相应研究。为此,本文通过考虑不同社交网络中用户相互联系的行为,建立相应的网络病毒传播动力学模型,进一步揭示由于不同社交网络间用户交互行为引起的网络病毒传播规律,从而提出对应的防御策略。

1 模型建立

本章采用经典的SI(Susceptible-Infected)模型来建模不同社交网络用户行为相互感染的网络病毒传播过程。在SI模型中,网络中节点的状态分为两种:1)易感染状态S，表示节点用户对网络病毒没有免疫功能,一旦和已感染节点接触就会被感染。2)已感染状态I，表示节点用户已经被网络病毒感染,而且具有感染其他用户的能力。在任意时刻t,网络中的节点处于这两种状态中的其中一种。

图1 节点状态转化图Fig. 1 Transition among states of nodes

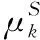
(1)

(2)

其中:

k=1,2,…,n}

假设,n阶矩阵B=(βkj)n×n是不可约的。式(1)的可行区域为:

2 模型分析

本章通过求式(1)的平衡点,确定模型中S和I的取值,进一步确定由模型(1)反映的控制网络病毒传播的临界值。从而为有效控制网络病毒传播提供理论指导。

根据平衡点的定义,令

可求得式(1)的免疫平衡点:

E0=(S0,0)

其中:

定理1 如果R0≤1,那么免疫平衡点E0在可行区域C内全局渐近稳定。

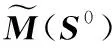
对L求导,得

如果R0=1,那么L′=0表明:

(ω1,ω2,…,ωn)

(3)

式(3)有唯一的平衡解I=0，所以,当R0≤1时,L′=0等价于I=0或S=S0。根据LaSalle’s不变集原理,可得,当R0≤1时,免疫平衡点E0是全局渐近稳定的。

证毕。

考虑到网络安全防御者关心的是如何控制网络病毒的快速扩散,保证网络正常运行,本文在理论分析部分只研究免疫平衡点的性态。

3 仿真验证

为了观察微分方程(1)刻画的网络病毒的传播过程,本章采用龙格-库塔(Runge-Kutta)法对微分方程(1)进行数值求解,在Matlab2016R环境下进行仿真验证。模型(1)中的参数分为两种类型:系统参数(bk和μk)和状态转换参数(除bk和μk之外的其余参数),其中系统参数反映网络空间要素的运行状态,状态转换参数反映社交网络中用户行为以及反病毒措施对网络病毒扩散的影响程度。另外,系统的初始状态,即S(0)和I(0)对网络病毒的扩散也会产生很大影响。不失一般性,实验时假设I(0)的取值较小。仿真实验主要是:1)验证针对模型(1)的理论分析的正确性;2)在确定系统参数值的情况下,通过改变状态转换参数的值来观察模型(1)反映的网络病毒传播过程;3)比较用户活跃的社交网络数量对网络病毒传播的影响;4)本文模型和传统模型之间的比较。

图2 R0=0.547 5<1时已感染节点比例随时间变化Fig.2 Infected nodes’ ratio versus time when R0=0.547 5<1

从图2可以看出,随着时间的演化,最终每个社交网络中被感染节点数都趋于0,也就是网络病毒的扩散被完全控制,与理论分析结果相符。同时,图中三条曲线的变化趋势都是在开始0～100的时间段内被感染节点数迅速增大,随后逐渐减小直至趋于0,这是因为,开始时,社交网络中易感染节点较多,被感染的风险就会较大,转换为已感染节点的速度也会快一些,随着易感染节点数的减少,转化为已感染节点的数量也会随着减少,直到趋于0,成为一个稳定状态。

2)然后,通过实验观察感染率βkj的变化对网络病毒扩散规模的影响。

取βkj为10-2数量级,即:β11=0.008,β12=0.003,β13=0.003,β21=0.003,β22=0.002,β23=0.002,β31=0.003,β32=0.004,β33=0.002,其他参数值和初始值都不变(同图2),计算得R0=2.384 9>1。仿真结果如图3所示。从图3可看出,当基本再生数R0的值大于1时,网络病毒不会被完全控制,而是稳定于一个正数。这个结论在已有工作中已得到证实[13],说明这一定律在交叉感染模型中仍然成立。而且,与图2相比,发现增大感染率后,病毒感染的速度大幅提升,在最初0～50的时间段内,迅速达到最高值,随后逐步下降到一个稳定的正数。这一结论与实际经验相符。

图3 R0=2.384 9>1时已感染节点比例随时间变化Fig. 3 Infected nodes’ ratio versus time when R0=2.384 9>1

3)为了观察用户活跃的社交网络个数对网络病毒扩散的影响,取参数n=2(k=1,2),考虑到家庭群成员相对较固定,而且人员数量也相对较少,所以保留工作与朋友群为活跃群,即去掉反映家庭群的所有参数,其他参数值与图2的参数取值相同。为了保持和图2的网络总节点数相同,设置Sk的初始值分别为42和100;Ik的初始值分别为4和6,其中：k=1代表由同事构成的社交网络;k=2代表由朋友构成的社交网络。仿真结果如图4所示。

图4 只考虑两个社交网络时已感染节点比例随时间变化Fig. 4 Infected nodes’ ratio versus time when considering two social networks

图4表明,当用户活跃的社交网络数为2时,网络病毒的扩散在短时间内会达到最大值,随后快速降低,直到趋于0。与图2相比,病毒爆发得快,控制得也快。而且在图4中被感染节点最大值的比例超过了图2,也就是说在病毒爆发初期,用户所在的社交网络数越多,越不利于病毒传播,但是,在病毒衰减期,社交网络数越少,越容易被控制。

4)最后,将本文模型与传统模型进行比较,仿真结果如图5所示。传统模型曲线n的取值为1，本文模型曲线n的取值为2，其余参数的取值如表1所示。观察图5发现,在病毒传播初期,本文模型反映的网络病毒扩散态势要比传统模型弱一些,这说明用户分布于不同的社交网络要比集中于一个网络更有利于缓解网络病毒的扩散,而在病毒衰减期,呈现出的是相反的态势。图5和图4呈现出了相同的规律。这一现象与文献[4]中提出的把大网络分割为不同小网络有利于控制网络病毒扩散的结论一致。

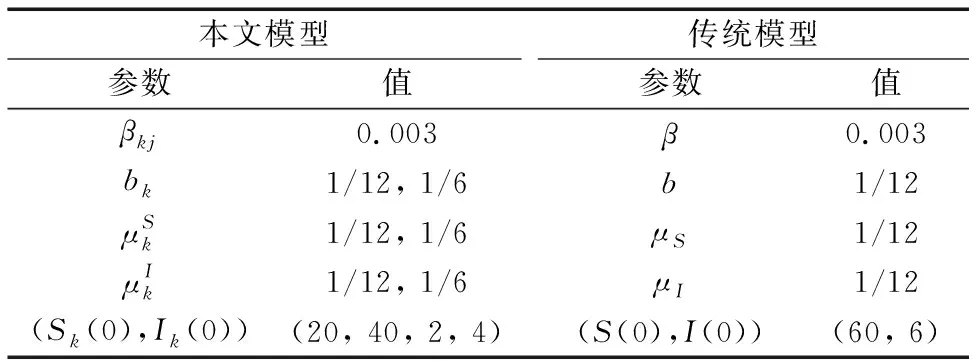
表1 图5中模型各参数取值表Tab. 1 Parameters values of Fig. 5

图5 本文模型与传统模型的比较Fig. 5 Comparison between proposed model and traditional model

4 结语

社交网络已经成为人们利用互联网进行工作、交流和生活的活跃平台，由不同社交网络间用户交互行为引起的网络安全问题也日益明显。本文构建了不同社交网络间用户交互行为引起的网络病毒传播动力学模型。该模型与已有病毒传播模型[7-8]的不同之处在于考虑了社交网络间的交叉感染。利用微分方程稳定性理论分析了模型反映的网络病毒传播的动力学性态,得到了控制网络病毒扩散的基本再生数R0的阈值，当R0的值小于等于1时,网络病毒会被完全控制，这与不考虑交叉感染的已有模型结论一致。最后,数值仿真实验验证了理论分析的正确性。同时,通过取不同参数值进行模拟,发现网络病毒传播的态势是由基本再生数直接决定的,只要基本再生数R0的值小于1,病毒扩散最终就会被控制；相反,当基本再生数R0的值大于1时,病毒在网络中会一直存在。另外,仿真结果表明,在网络节点总数相同的情况下,用户在社交网络中越分散,越有利于缓解网络病毒的爆发。

今后,将对不同活跃用户参与的社交网络数,以及对敏感信息处理的态度进行调研和统计分析,进一步检验模型的实际应用价值。