基于自步学习的无监督属性选择算法

龚永红，郑 威，吴 林，谭马龙，余 浩

(1.桂林航天工业学院 图书馆，广西 桂林 541004； 2.广西师范大学 广西多源信息挖掘与安全重点实验室，广西 桂林 541004)(*通信作者电子邮箱zwgxnu@163.com)

0 引言

伴随信息采集技术的不断发展，具有大样本、高维度特点的大数据已经普遍应用于模式识别和机器学习等领域中[1-2]。高维大数据不仅提升了数据处理的成本，而且数据中存在的冗余属性还会影响数据处理的效果，此外还可能造成维度灾难等问题[3]。在高维大数据的研究中，大数据知识挖掘或者数据认知模式建立之前，合理地移除数据中的冗余属性和噪声样本，能够有效提高知识获取的准确性，因此数据降维成为了一个重要的研究领域[4-5]。属性选择方法[6]是一种重要的数据降维方法，按照学习方式的不同可分为三类：有监督学习[7]、无监督学习[1,8-10]和半监督学习[11-12]。在现实应用中，获取数据的类标签是十分困难的，通常需要消耗大量的人力物力，因此无监督学习更具有实际应用价值。

高维大数据除了包含冗余的属性外，往往也包含了噪声样本。由于数据降维方法只考虑样本之间的共同性(即所有样本都包含有用信息)，却忽略了样本的差异性(即不同样本拥有不同的重要性)[13]，因此，不能有效避免数据中噪声样本对模型的影响而导致获得的属性选择模型并不理想。根据文献[2,14]的研究表明，属性选择方法对冗余属性具有良好效果，而自步学习方法对噪声样本的处理具有显著效果。因此，本文通过结合无监督属性选择和自步学习两种学习理念，提出了一种新的属性选择模型——基于自步学习的无监督属性选择(Unsupervised Feature Selection base on Self-Paced Learning, UFS-SPL)算法，能够同时在样本层次和属性层次进行有效筛选，挖掘数据内在的认知模式，提高属性选择模型的学习能力。

本文首先使用属性自表达方法获得自表达系数矩阵实现无监督学习；然后利用L2,1-范数惩罚自表达系数矩阵去除冗余属性，实现属性选择的目的。此外，在属性选择框架中添加自步学习正则化项，通过考虑样本的共同性和差异性，使得目标函数首先自动选取重要的样本子集进行模型学习，然后通过迭代学习方式从剩余样本中逐步选择次要样本训练模型从而提升模型泛化性能，直至所有样本均参与模型训练或者模型性能降低。通过考虑样本的差异性并依据样本重要性逐步对模型进行训练，本文提出算法能够降低噪声样本对训练过程的干扰，因此可以保证最终获得的属性选择模型同时具有健壮性和泛化性。此外，本文提出了一种简单有效的优化方法，能够使目标函数快速收敛。由于本文采用自步学习方法对数据进行抽样训练，所以比传统的属性选择方法具备更好属性选择效果。实验结果表明，相较于常规属性选择算法，通过本算法获得的新属性集在聚类分析上具有更良好的表现。

1 相关理论

1.1 稀疏属性选择

稀疏学习[15]因其强大的内在理论以及应用价值被引入机器学习等领域并获得广泛应用，而属性选择的目标是在所有属性中寻找一个最能描述样本的属性子集。所以将稀疏学习理论应用到属性选择方法中，通过稀疏表示方法约束获得的属性权重，最终通过稀疏解进行属性选择。稀疏学习的引入可以实现属性的自动选择，因此能在去除冗余和不相关信息的同时保留重要特征。基于稀疏表示的属性选择方法可以表示为：

(1)

其中：L(x,w)是损失函数；φ(w)是稀疏正则化项；α是稀疏控制参数,α值越大w就越稀疏,反之亦然。

选择有效的稀疏正则化因子能够提升稀疏属性选择的性能。在稀疏学习中，最有效的稀疏正则化因子是L0-范数，但由于其难以优化求解(NP难问题)，故许多文献采用L0-范数的最优凸近似L1-范数代替。L2,1-范数正则化因子能够促进行稀疏，可以在移除冗余及不相关属性的同时有效地降低离群点的影响，所以本文采用L2,1-范数代替L1-范数作为正则化项，而且求解L2,1-范数正则化项是凸优化问题，故能够保证本文模型获得全局最优解[2]。

1.2 自步学习

受到学习方式的启发，文献[13]提出了课程学习理论并建立了一种由简到难的学习框架，其核心思想是通过模拟人的学习过程，首先从简单的知识学起，然后逐渐增加学习难度，最后学习更困难、更专业的知识。而自步学习则是使用数学形式表达课程学习理论的方法。

给定数据集X∈Rn×d及对应响应矩阵Y∈Rn×c；L(yi,f(xi,w))表示损失函数，φ(w)为变量w的正则化项；v=[v1,v2,…,vn]表示自步权重向量，其中vi∈[0,1]为二分变量用于表示第i个样本是否被选择；φ(v)为自步学习正则化项。基于自步学习的目标函数可写为：

(2)

s.t.v∈[0,1]n

其中:α为稀疏正则化控制参数；λ为样本选择控制参数。

自步学习根据预测误差(损失值)来定义样本的重要性，通常将不存在预测误差或者小于一定阈值的样本定义为重要样本(即“简单”样本)，而将预测误差较大的噪声或异常值定义为次要样本(即“困难”样本)。将自步学习方法融入到属性选择中，能够更有效地避免噪声样本参与属性选择模型的训练，最终获得具有鲁棒性与泛化性的训练模型。

2 算法描述与优化

2.1 算法描述

假设给定数据集X∈Rn×d，其中n和d分别为样本和属性的数量。不同于有监督学习，无监督学习由于缺少类标签引导学习，导致无法直接通过拟合响应矩阵Y与样本矩阵X获取属性权重矩阵。虽然可以将属性选择问题转化为多输出问题，即通过计算样本间的相似性或流形结构的方法建立响应矩阵，但是想要选取一个合适的响应矩阵仍然比较困难。

实际上，每个属性都可以通过其他属性的线性组合去近似表示，因此，本文利用X代替Y作为响应矩阵建立属性自表达关系：

X=XW+E

(3)

选择适当的稀疏正则化因子可以有效地去除冗余属性和离群点的影响。由于L2,1-范数可以引导行稀疏，可以迫使系数矩阵W中对应不重要特征的系数趋近于零或直接等于零，从而去除无关属性，实现属性选择的目的。故本文采用L2,1-范数作为稀疏正则化项，得到的无监督属性选择的目标函数为：

(4)

虽然式(4)可以有效移除冗余属性从而达到属性选择的效果，但是采用全体样本进行训练不仅会造成计算资源的浪费,而且其中包含的噪声样本也会影响模型的训练。

虽然简单随机抽样方法可以缓解资源消耗的问题，但其既无法避免噪声数据的影响，也不能兼顾样本间的共同性和差异性，这不仅不能优化模型的训练，还有可能因为样本信息的缺失而导致模型训练的失败。因此，本文融合自步学习方法与无监督属性选择两种学习模型，首先通过训练获取重要样本，然后再通过重要样本训练获得重要属性，由于没有噪声样本的影响而提升属性选择的准确性，其目标函数为：

(5)

s.t.v∈[0,1]n

其中:k为自步学习参数，用于决定自步学习过程中参与训练的样本。当k值较大时，自步学习倾向于选择拟合误差较小的样本进行训练；当k值逐渐减小就会有越来越多的样本被选择。因此，自步学习是一种由简到难的学习模式，也是一种能够有效避免噪声数据的抽样方式。

式(5)通过分配给每个样本一个二分权重(vi为0或1，其中i=1,2,…,n)实现了“硬性”的样本选择，但是由于数据中的噪声样本并非均匀分布在所有样本中，所以硬权重并不能精准判断是否选取样本。而软权重分配给每个样本一个0～1的实数值(包括0和1)，这样能够更加真实地反映训练中样本的潜在重要性，因此比硬权重具有更好的抽样效果[16]。使用软权重自步学习正则化因子替换原有正则化项，得到最终目标函数为：

(6)

s.t. 0≤vi≤1;i=1,2,…,n

其中：β为区间控制参数；k为自步学习参数。软权重自步学习正则化项能够通过更精确选取样本，进一步避免噪声样本的影响，从而获得更优秀的属性选择效果。

本文提出的UFS-SPL算法具有以下优点：

1)本文算法使用属性自表达方法建立模型不仅解决了无监督学习中响应矩阵难以确认的问题，而且该方式对离群点并不敏感，因此具有良好的鲁棒性和泛化性；而且在自表达模型中引入L2,1-范数实现行稀疏能够有效地移除冗余属性，使模型能够自动选取重要属性。

2)加入了一种新的样本训练模式。自步通过模拟人或动物的学习机制，实现了一种由简到难的学习方式；在传统的无监督属性选择中添加自步学习正则化因子，可以避免噪声样本对模型训练的影响，提升属性选择模型的鲁棒性。

3)使用了软权重自步学习正则化因子进行样本抽样。不同于硬权重正则化因子使用二分权重(选择样本的权重为1，否则为0)，软权重在硬权重的基础上添加了“模糊区间”(权重值为0～1)[17]，这不仅可以细化样本的抽样，而且还可以进一步降低噪声样本在训练中的影响，从而提高属性选择模型的效果。

4)UFS-SPL在迭代过程中对样本进行逐步抽样，并且通过对某一迭代过程所选择的样本进行优化获取当前最优解，直到所有样本参与训练并获得最终的全局最优解。

本文算法流程如下：

1)获取自表达系数矩阵W∈Rd×d。

输入 训练样本X∈Rn×d，控制参数α、β、k、k_end，步长参数μ>1。

输出 系数矩阵W∈Rd×d。

①如果k≤k_end，则退出。

②通过式(14)获取v(t);

③根据式(11)获取W(t);

④通过式(10)更新D(t+1)；

⑤更新参数k=k/μ，t=t+1；重复以上步骤。

2)计算每个属性权重θi(θi=‖wi‖2),其中wi是系数矩阵W的第i行。

3)对属性权重θ按降序排序并选取前c个权重对应的X的特征向量组成新的属性集。

2.2 算法优化

本文UFS-SPL算法包含两个变量，因此采用两步交替优化法分别优化：

1)固定v，优化W。

当固定v后，目标函数(6)变为：

(7)

为方便优化，将式(7)改写为：

(8)

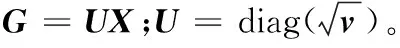
式(8)可以看作关于W的函数，因此，对式(8)进行求导，并且使导数为0得到：

-GTG+GTGW+αDW=0

(9)

其中D为对角矩阵，它的每一个元素：

(10)

通过简单数学变换得到最终解为：

W=(GTG+αD)-1GTG

(11)

2)固定W，优化v。

当固定W后，原目标函数可写为：

(12)

s.t. 0≤vi≤1;i=1,2,…,n

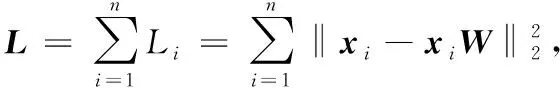
(13)

s.t. 0≤vi≤1;i=1,2,…,n

通过式(13)可以得到v的解为：

(14)

3 优化算法收敛性证明及参数决定

3.1 收敛性证明

由于式(8)是非平滑的，使得对W的优化求解变得困难，但本文使用了一种简单有效的算法来求解该问题，下面将给出算法第t次迭代中优化矩阵W的收敛性证明。

假设算法的第t+1次迭代结果为：

(15)

在求得第t+1次的解W后,可以得到：

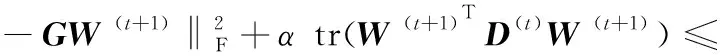
(16)

将式(8)得到的对角矩阵代入到不等式(16)，得到：

(17)

对于W(t)和W(t+1)的每一行，可以得到下列不等式：

(18)

在累加后并乘以控制参数α可以得到：

(19)

最后，结合不等式(17)、(19)可得到：

(20)

由式(15)～(20)可知，目标函数的值在优化过程中保持单调递减，所以本文提出的优化算法可以在当前所选择的样本下使目标函数稳定收敛从而获得全局解。

3.2 参数设置

由式(14)可知，参数k和β的值决定了学习过程中样本的选取，因此，选择合适的参数可以提升自步学习的效果。假设第一次被选入样本的最大损失值为LS，根据式(14)可以得到：

(21)

为简化计算，令k=1/β，可以得到：

(22)

根据式(22)可以得到:

(23)

由式(22)与(23)可知，本文方法可以根据初始选取的样本的数量获取合适的参数，因此，可以降低本文算法对参数的依赖。在固定参数k和β之后，其他参数仍需要调整，本文将在实验部分给出具体的参数设定。

表2 不同算法在不同数据集上准确率、互信息、纯度统计 %Tab. 2 Accuracy, mutual information, purity statistics of different algorithms on different data sets %

4 实验结果与分析

4.1 实验设置

本文使用6个真实数据集测试提出属性选择算法的性能，其中数据集Umist、Isolet来源于UCI(UCI machine learning repository)[20]，USPS来自手写数字数据库[21]，Jaffe来自人脸图像数据库[22]，Coil、DBword来自属性选择数据库[23]，数据集的详细信息见表1。

本文实验使用Matlab 2014a软件在Windows 10系统下进行测试。为验证本文算法的有效性，本文实验选择4种对比算法进行比较：1)NFS(Non Feature Selection)方法，对不经属性选择的数据直接进行k-means聚类。2)凸半监督多标签属性选择(Convex Semi-supervised multi-label Feature Selection, CSFS)方法[18]，通过真实标签构造的预测标签去拟合数据获得属性权重，并且使用L2,1-范数对权重矩阵进行稀疏处理。3)正则化自表达(Regularized Self-Representation, RSR)方法[10]，通过自表达方法使用样本矩阵代替响应矩阵，然后嵌入到稀疏回归模型进行属性选择。4)无监督属性选择的耦合字典学习方法(Coupled Dictionary Learning method for unsupervised Feature Selection, CDLFS)[19]，依据矩阵分解的思想构造分解字典矩阵与合成字典矩阵进行无监督属性选择。

在参数设置方面，本文算法中的稀疏控制参数α=10-3,10-2,…,103，自步学习步长参数μ>1。对于其他对比算法，本文均按照其原实验参数进行设置。

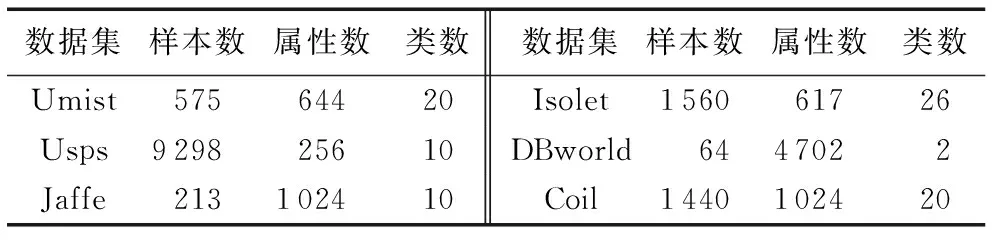
表1 数据集信息统计Tab. 1 Dataset information statistics

4.2 实验结果与分析

在本文实验中，除NFS外，利用所有属性选择算法对数据集属性的重要性进行学习，并且依据重要程度排序，选择前[20%，40%，60%，80%]的属性作为新的属性集，然后分别进行k-means聚类，选取最优结果作为最终结果。本文采用准确率、互信息、纯度3种评价指标评估所有算法的效果。表2分别展示了所有算法在6个真实数据集上的准确率、互信息和纯度。

通过分析表2可以看出，在全部数据集中,本文提出的UFS-SPL方法在三项评价指标上相较于CSFS、RSR、CDLFS方法平均提高了12.06%、10.54%和10.5%。具体地，在聚类准确率上UFS-SPL方法分别比NFS、CSFS、RSR、CDLFS四种算法提升了20.38%、12.20%、11.29%、12.68%，因此，可以验证本文方法比使用传统训练方式的属性选择方法拥有更好的性能。特别地，在数据集USPS(样本最多)和DBworld(维度最高)上，本文方法均获得良好的表现，准确率不但比NFS分别高出26.88%和11.54%，而且与CDLFS算法相比分别提高15.02%和8.18%，这是因为UFS-SPL算法充分考虑了样本的共同性和差异性，在降低噪声样本干扰的同时去除冗余信息，因此，在处理多样本与高维度的数据上能取得更好的效果。表2还展示了各算法在互信息与纯度的对比结果，本文算法的效果仍然均超过其他对比算法，进一步说明本文算法的鲁棒性。

图1 不同参数下准确率的直方图Fig. 1 Histograms of accuracy under different parameters

图2 不同样本数下的聚类准确率Fig. 2 Clustering accuracy under different samples

图1为不同参数下准确率的直方图，可清楚地看到本文UFS-SPL算法通过设置不同的参数可以获得不同的效果。从图1可以看出：当设置参数α=10-3并且设置参数μ=1.4时，本文方法在数据集USPS上获得最佳表现。这说明了UFS-SPL算法对于参数是敏感的，因此通过调节参数可以获得更好的效果。

图2为不同样本数下的聚类准确率，从中可以看出：1)非抽样方法由于采用所有样本进行训练，相对随机抽样方法来说模型的泛化性更强；但由于缺少对样本重要性的判别，所以难以获得更有效的模型。2)随机抽样方法由于没有考虑样本间的共同性和差异性，造成结果同样存在随机性。3)自步学习方法能克服随机抽样方法不稳定且不易获得好结果的缺点，该方法可以首先选择重要样本进行模型训练，获得健壮的初始属性选择模型，然后通过不断添加次要样本进一步提升模型的泛化性能，从而获得最好的属性选择效果。

因为不同的数据集具有不同的数据分布，往往所含有的干扰因素也是不同的。实验结果表明，本文UFS-SPL算法在不同数据集上均获得了更好的效果,因此，UFS-SPL算法能够输出更具有判别力的属性子集，模型具有更强的鲁棒性。

5 结语

本文通过结合属性自表达、稀疏学习和自步学习提出了一种新的无监督属性选择方法——UFS-SPL算法。本文算法通过在稀疏属性选择框架中引入自步学习对数据进行迭代抽样，选择重要样本参与模型训练，有效避免了噪声样本带来的干扰，从而更加准确地捕捉重要属性，提升属性选择的准确性。经实验验证，本文算法可以获得鲁棒的属性选择模型。在今后工作中，将尝试在本文算法中添加图正则化以进一步提升属性选择算法准确性，并尝试拓展算法到半监督学习中。