基于Matlab的SINS算法仿真
沈阳理工大学 王海生
为了使实际SINS(捷联惯导系统)算法仿真程序编写更加方便,列写了一些与SINS更新算法有关的函数计算公式。对SINS算法进行了仿真,仿真结果与理论分析结论吻合。
1.引言
SINS算法的核心部分是姿态更新解算,由于四元数算法的优良特性,它在工程上常被采用。本文总结了与SINS算法有关的函数计算公式,对SINS算法进行了仿真,为SINS/GPS组合导航的研究打下基础。
2.SINS算法
本文选用地理坐标系为导航坐标系,记为n系,载体坐标系记为b系。
2.1 SINS更新算法
SINS更新的基本理念是,把前一时刻的姿态、速度和位置等导航参数作为初值,利用前一时刻至当前时刻的惯性器件采样输出,解算此时刻的导航参数,作为下一时刻SINS解算初值,如此反复。惯性器件采样经过误差补偿后获得等效旋转矢量和比力速度增量,再经过以下三步骤便可实现SINS更新,计算公式为:
(1)速度更新算法

位置更新算法

(3)姿态更新算法

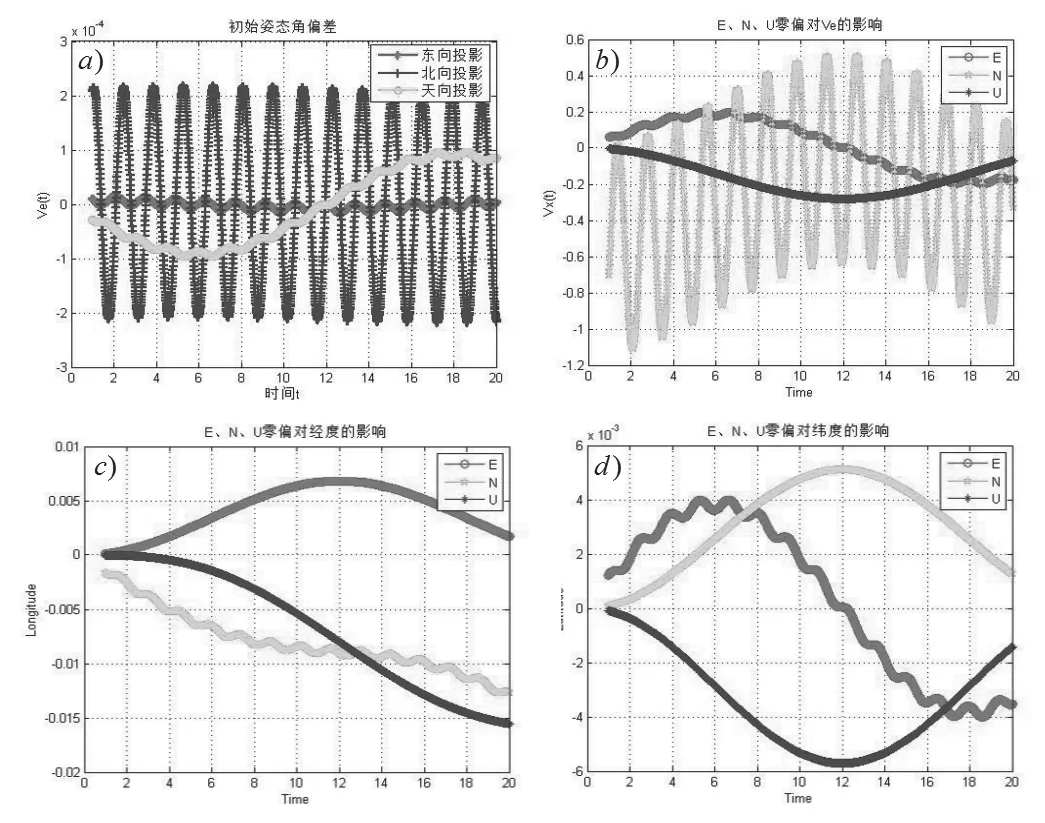
图1 陀螺漂移对导航精度的影响

图2 捷联惯导算法仿真
2.2 SINS速度与位置误差分析
速度与位置是积分关系,二者紧密相连,在误差上也是递推的。
速度误差的递推关系式是:
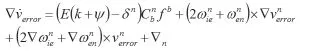
位置误差:

3.SINS仿真与分析
以ENU坐标系为导航坐标系,在41.5纬度下仿真东、北、天三方向的初始姿态误差、初始位置误差和加速度计零偏误差对导航精度的影响,结果如图1所示。
由仿真图可知,东向速度精度受初始姿态偏差北向投影和初始北向零偏影响较大;经度精度受初始东向零偏影响较大;纬度精度受初始北向零偏和天向零偏影响较大。而且由于地球自转和地球加速度的影响,速度和姿态都会发生略微偏差。
图2中,速度误差和位置误差小图中,高度通道的误差为红色发散曲线,而水平平台误差、经纬度和水平速度误差呈现振荡趋势,方位平台误差变化比较小。
4.结束语
总结了一些SINS算法的计算公式,对SINS算法进行了仿真分析。SINS仿真结果与INS误差理论分析结论向吻合。证明了所设计算法是正确的。

