电力系统潮流计算算法研究

安徽理工大学电气与信息工程学院 秦 孜 秦晓佳 王梦伟

首先本文简单介绍了潮流计算的原理及意义，电力系统稳态运行以及故障分析时都需要提前进行潮流计算。随后对采用极坐标牛顿法潮流计算的过程做了简要分析。最后，对13节点的编程计算结果表明，运用极坐标牛顿法进行潮流计算缩短了迭代次数，精度可达。

0 引言

电力系统潮流分布一般指正常稳态运行时的功率分布与电压分布，对潮流分布的计算称为潮流计算。该计算是电力网络设计及运行中最基本的计算，其目的在于对用户电力供应的质量以及电力网运行的安全性预测和经济性评估提供基础数据。通过对电力网络进行潮流计算，可以得到各母线上电压的大小与相位，各电力网功率分布以及功率损耗（陈珩.电力系统稳态分析[D].中国电力出版社,2007）。

高斯赛德尔法是早期进行潮流计算的一种算法，它对初值的选择并不敏感，能够稳定的算出结果。但缺点是运算速度较慢，因此实际计算中并不单独使用。牛顿拉夫逊法因具有使用运算内存较少，收敛性好，运算速度较快等特点受到人们的欢迎。实际中，研究人员通常先用高斯赛德尔法得到一个合理的初值，然后使用牛顿拉夫逊法进行迭代来完成系统潮流计算。

本文主要对牛顿拉夫逊法进行讨论与研究。通过其数学模型了解该算法的执行过程，并通过实际电网接线图对该算法迭代过程进行分析。

1 电力系统潮流计算

节点分类：

根据初始变量的不同，可将系统中的节点分为以下类型：第一类称为PQ节点。这种节点的注入有功功率和无功功率是给定的，当发电机达到无功出力极限时发电机节点可以选为该节点。因此，该节点数目众多。第二类称为PV节点。由于等值负荷和等值电源的有功功率是给定的，从而注入有功功率是给定的，通常选择有一定无功功率储备的发电厂的母线作为PV节点。该类节点在电力系统中数量很少，有些情况下没有此类节点。第三类称为平衡节点。这类节点的等值负荷功率、电压幅值和相角都是给定的，它的有功、无功的注入完全没有限制。该节点的选定是作为潮流计算时的参考，因此是必须存在的。担负调整系统频率的任务的发电厂母线往往被选作平衡节点（姚振宇.平衡节点设置对电力交易公平性的影响[D].华北电力大学(北京),2008;胡建,杨宣访,陈帆.基于牛顿-拉夫逊电力系统潮流计算的改进算法[J].计算技术与自动化,2013,32(04):41-44）。

2 牛顿拉夫逊法

2.1 牛顿迭代法潮流计算原理

求解功率方程的式子如下：

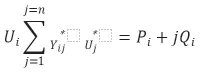
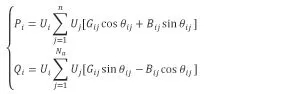
式中i=1,2…,n为节点数。Pi为PQ节点与PV节点的注入有功；Qi为PQ节点的注入无功；Ui为PV节点电压。

2.2 牛顿迭代法潮流计算步骤

（1）由网络接线列出节点导纳矩阵。

（2）给定各节点电压的原始值。

（3）将节点电压的初始值代入功率方程展开式，求出修正方程各节点功率以及电压偏移。

（4）求解雅可比矩阵中各元素。

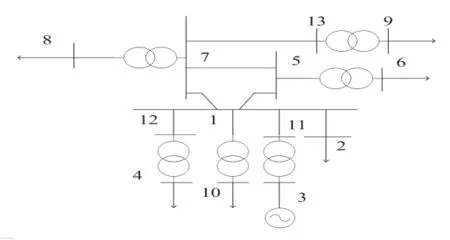
图1 节点接线图

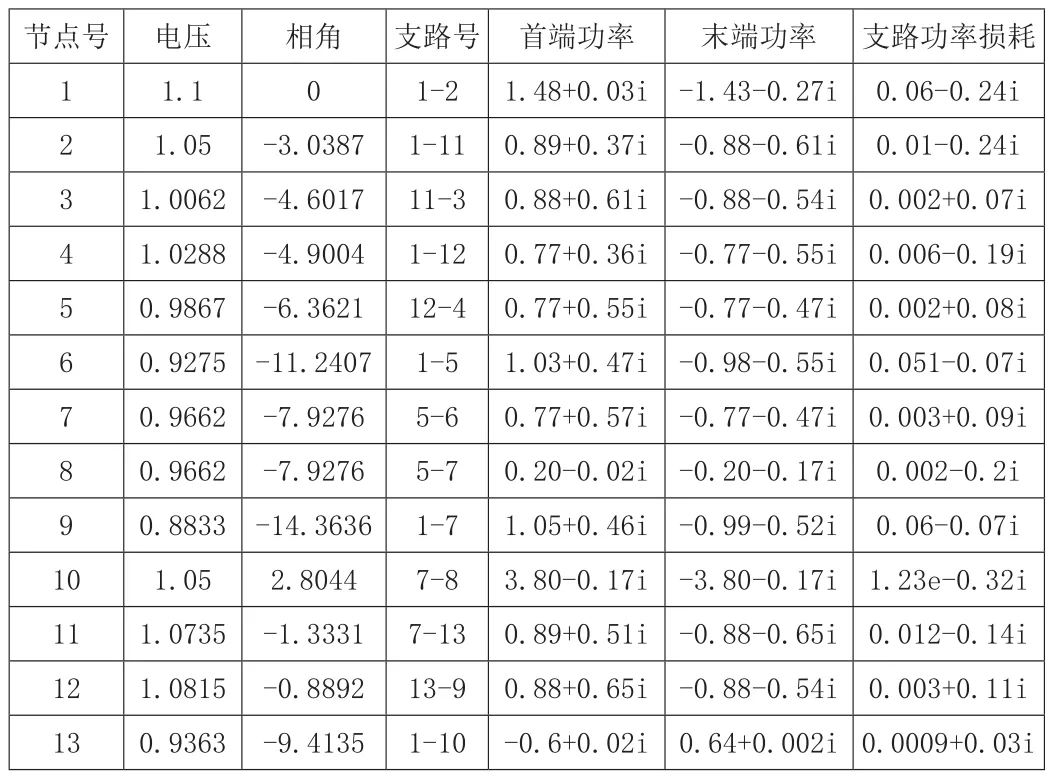
表1 计算机运行结果表

（5）解修正方程式，求出电压修正量。

（6）求出电压新值，进入下一次迭代。

（7）输出平衡功率与线路功率。

3 实例分析

本文通过某地区实际电网参数设计的13节点网络图来实现牛顿拉夫逊法的应用。该系统有一台发电机，六个变压器。仿真结果如图1、表1所示。

4 结束语

本文首先对电力系统潮流计算工作原理进行了分析，比较分析高斯赛德尔法与牛顿拉夫逊法的优缺点。随后阐述了牛顿拉夫逊法的基本流程，最后通过实例说明了牛顿拉夫逊法具有迭代迅速，易于收敛等特点。