人工免疫算法在机器人路径规划中的研究

南京大学金陵学院 孙海洋 郭黎黎 谢鹏飞 王先一

Aiming at the shortcomings of traditional immune algorithm applied to robot path planning, such as premature convergence, easy to fall into local optimum and weakening of late acquisition ability, this paper introduces clonal selection operator and selects clone according to the affinity of antibody in the population. The improvement of the antibody using high frequency variation is also made. The Matlab is used to build the robot path planning simulation platform. In the grid map environment, the traditional algorithm and the improved algorithm are compared and simulated. The simulation results show that the artificial immune algorithm is improved, which avoids local convergence and improves the convergence speed. The planning path is closer to the optimal path, and the search range is expanded, and problems such as poor local search ability are improved. Verify that the improvements proposed in this paper is feasible and effective.

针对传统免疫算法应用于机器人路径规划中，存在的早熟收敛、容易陷入局部最优及后期收索能力减弱等缺陷，本文引入克隆选择算子,按照种群中抗体亲和度的大小进行选择克隆，并对抗体采用高频变异的方式进行改进。使用Matlab搭建机器人路径规划仿真平台，在栅格地图环境下，对传统算法和改进算法进行对比仿真分析，仿真结果表明改进后的人工免疫算法，有效地避免了局部收敛，提高了收敛速度，所规划路径更接近最优路径，并且扩大了搜索范围，改善了局部搜索能力差等问题。验证了本文所提改进方案的可行性和有效性。

1 引言

人工免疫算法模仿生物免疫系统的过程，而提出的一种启发式随机搜索算法，其具有全局并行分布式搜索、多样性保持机制和鲁棒性强的特点。在对问题的解进行局部搜索的同时利用变异算子和种群刷新算子产生新个体使得算法可以在可行解区间内进行搜索，是一个全局优化能力的算法，具有全局收敛性能。生物免疫系统与人工免疫算法概念对应关系，如表1所示。

表1 生物免疫系统与人工免疫算法概念对应表

人工免疫算法在机器人路径规划中具有重要研究价值，但直接把传统的免疫算法应用于机器人路径规划方案中，会存在容易陷入局部最优，而非全局最优，以及收敛速度慢等缺陷。

2 免疫算法基本概念

2.1 人工免疫算法原理

人工免疫算法将生物免疫过程中的进化链（产生抗体群→计算亲和度→选择克隆→变异→计算抗体浓度→促进/抑制→更新抗体群）抽象成为数学上的进化寻优过程。

2.2 人工免疫算法流程

Step1 抗体识别：将待优化的问题抽象为抗原形式。

Step2 产生初始种群：随机产生初始种群。

Step3 计算亲和度：通过计算抗体与抗原之间的亲和度，选择亲和度大的抗体进行增殖。

Step4 终止条件判断：如果满足条件则算法终止；否则继续寻优运算。

Step5 计算抗体浓度和激励度：计算抗体群的浓度，促进浓度低且具有较高亲和度的抗体，抑制浓度高且具有较低亲和度的抗体。

Step6 更新抗体群：用亲和度高的抗体代替亲和度低的抗体，产生新的抗体。

Step7终止条件判断：若得到最优解则结束，否则返回Step3。

人工免疫算法的流程图如图1所示。

图1 人工免疫算法流程图

2.3 人工免疫重要算子

（1）抗体i与抗原亲和度

亲和度是免疫算法中最重要也是最复杂的计算，通常，其计算如公式（1）所示。

其中，ti是抗原与抗体i的结合强度，(Ag)i是抗体i与抗原之间的亲和度，其值介于0和1之间。当(Ag)i=1（ti=0）时,表示抗体i与抗原匹配度极高，即该抗体为最优解。

（2）抗体浓度

在人工免疫算法中采用基于抗体浓度调节的机制来保持种群中抗体的多样性。在免疫调节算法中，那些高抗原亲和度且样本浓度较低的抗体将被增强；相反，那些低抗原亲和度且样本浓度较高的抗体将被抑制。抗体浓度的计算如公式（2）所示。

其中，(Ag)i表示抗体i与抗原的亲和度，θ为亲和度常数，一般取值为0.9 ≤ θ ≤ 1，M表示亲和度大于θ的抗体个数，N为抗体总数。

（3）交叉算子

交叉通常又称为重组，是以较大的概率从种群中选择两个个体，对两个个体编码串上的某个或某些位进行交换。交叉是产生新个体的主要方式。交叉操作方式主要有单点交叉、多点交叉、均匀交叉和算术交叉等。

（4）变异算子

变异通常以较小的概率对个体编码串上的某个或某些位进行改变，是产生新个体的辅助方式，但是必不可少的一个环节，它可以改善算法的局部搜索能力，并且可以维持样本的多样性，避免出现“早熟”现象。

交叉算子和变异算子相结合，可进一步保证算法的局部和全局搜索能力，从而使得免疫算法以较优的性能完成寻优过程。

3 基于传统免疫算法的机器人路径规划

3.1 环境建模

环境建模是机器人路径规划中的重要环节，目前常见的建模方式主要有人工势场法、栅格法、路标法等。采用20*20栅格地图对机器人运动环境进行建模，其中黑色栅格表示障碍物，白色栅格表示自由空间。

3.2 仿真验证

利用Matlab对基于传统免疫算法的路径规划方案进行仿真，设置仿真参数如下。

设置初始种群数为20，迭代次数为200，交叉概率为0.6，变异概率为0.2。仿真结果如图2(a)和图2(b)所示。

图2 （a）传统免疫算法的路径规划图

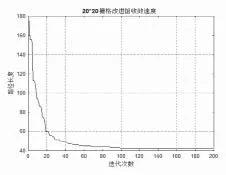
图2 （b）传统免疫算法的收敛曲线

通过观察图2（b）可以发现，该算法在第150次迭代时才趋于稳定，最短路径长度为42.0416。

4 免疫算法的改进

4.1 克隆算子和高频变异

（1）克隆选择算子：对种群中的抗体按照亲和度由高到低进行排序，选择亲和度高的抗体进行克隆繁殖。

（2）高频变异算子：克隆变异能够在父代抗体的种群内进行有效搜索的同时，通过变异操作使抗体群跳出局部最优，从而得到全局最优解。本文采用高频变异，即让亲和度较高的抗体进行高频变异，减少了相似抗体在种群的繁殖速度，从而提高了抗体种类的多样性，同时，也改善了克隆选择过程导致的算法收敛速度较慢的缺点。

4.2 算法流程图

Step1 抗原识别：识别环境并记录障碍物的信息，设置起始点和终点。

Step2 计算抗体亲和度：对抗体抗原的亲和度进行计算，亲和度的计算如公式（3）所示。

其中，ds表示机器人与障碍物之间的距离，de表示机器人到目的地的距离，X（0～2pi）是路线与机器人和终点连线的夹角。

Step3 终止条件判断：初始化时设置一个中间变量time和迭代次数N，time初始为0，如果N次迭代后得到了无碰撞的路径，则执行Step4，否则，令time=time+1。

Step4 克隆繁殖：根据种群中亲和度的高低进行排序，选择亲和度高的个体进行克隆繁殖。

Step5 克隆变异：以较高的概率对种群中的抗体进行高频变异操作。

图3 改进免疫算法流程图

4.3 仿真结果分析

定义初始种群数为20，迭代次数为200，交叉概率为0.6，变异概率设为0.8。即在相同的地图环境及仿真参数设置中，引入克隆算子，并将种群中抗体变异操作改为高频变异。仿真结果如图4(a)和图4(b)所示。

图4 （a）改进免疫算法的路径规划图

图4 （b） 改进免疫算法的收敛曲线

从图4(b)可以看出，改进后的算法大概在第10代就已经趋于稳定，路径长度为28.6274。改进后的算法与传统算法相比，不仅具有较高的收敛速度。而且最短路径长度也有较大缩短。

结束语

本文基于人工免疫算法的机器人路径规划方案，在传统免疫算法的基础上引入了克隆算子，并对种群中的抗体采用高频变异的方式，以便保持群体中抗体的多样性，扩大了搜索范围。通过Matlab仿真验证，改进后的算法无论在算法收敛还是所寻最短路径方面都取得了较好的性能。