四旋翼飞行器建模、仿真与PID控制

北京航空航天大学自动化科学与电气工程学院 陈听雨

四旋翼是一种实用的无人飞行器。本文首先对四旋翼进行了动力学分析，在其基础上建立了四旋翼的数学模型。在对模型进行化简后，设计了飞行控制系统，并将控制系统拆分为内环姿态控制与外环位置控制，分别设计了PID控制率对其进行控制。最后在Matlab/Simulink中搭建了完整的四旋翼飞行控制仿真模型，并对模型与控制率进行了仿真验证。

1.引言

四旋翼飞行器是一种能实现垂直起降的非共轴式多旋翼飞行器（李俊,李运堂.四旋翼飞行器的动力学建模及PID控制[J].辽宁工程技术大学学报(自然科学版),2012,31(1):114-117）。小型四旋翼飞行器具有四个螺旋桨，并且螺旋桨呈十字交叉结构的旋翼式飞行器，它通过调整四个电机的转速来实现俯仰、横滚、偏航等飞行动作，并具有可悬停、机动性好、结构简单等优点（江杰,岂伟楠.四旋翼飞行器建模与PID控制器设计[J].电子设计工程,2013,21(23):147-150）。

图1 四旋翼飞行器

与固定翼飞行器相比，四旋翼控制相对简单，只需调节其四个旋翼转速即可实现对四旋翼飞行姿态的控制。为使得四旋翼能够按照设计的姿态与轨迹进行飞行，必须首先对四旋翼进行建模，然后根据得到的模型设计飞行控制系统并进行仿真验证。因此，对四旋翼进行建模，在此基础之上设计合理的控制率，并进行仿真验证是四旋翼实现各种姿态与路径飞行的关键。目前，四旋翼的控制方法主要有反步控制、H∞控制与滑模控制等（王树刚.四旋翼直升机控制问题研究[D].哈尔滨:哈尔滨工业大学,2006;聂博文.微小型四旋翼无人直升机建模及控制方法研究[D].长沙:国防科学技术大学,2006;王丽新.基于滑模理论的四旋翼直升机的姿态控制研究[D].沈阳:东北大学,2009）。

本文对通过对四旋翼进行动力学分析，建立了四旋翼的动力学模型，并对其进行了化简。根据化简的模型，使用PID控制方法设计了四旋翼飞行控制率，并在Matlab/Simulink中对其进行了仿真验证。

本文共分为四个部分，第一部分对四旋翼与本文目的进行了简述，第二部分简要介绍了四旋翼动力学建模与简化的内容，第三部分完成了对四旋翼模型的仿真、PID控制率设计与验证，第四部分对全文进行了总结，并提出了未来工作的重点方向。

2.四旋翼动力学建模与简化

2.1 基本假设与坐标系变换

正常情况下，四旋翼飞行器结构呈X型。

图2 四旋翼飞行器结构

在为四旋翼建模之前，为简化模型分析，抓住主要矛盾，忽略次要矛盾，提出以下七点假设：

（1）四旋翼飞行器是刚体，在其飞行过程中质量保持不变；

（2）地面坐标系视为惯性坐标系；

（3）地球表面是平的，且忽略地球自转与公转；

（4）重力不随高度变化而变化；

（5）四旋翼飞行器形状与质量是关于中心对称的（吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005:46-47）；

（6）四旋翼低速飞行时忽略空气摩擦力；

（7）四旋翼进行低速小角度飞行。

首先为四旋翼建立合适的坐标系。

图3 地面坐标系与机体坐标系

其中，地面坐标系定义如下：选取地面上的一点，即四旋翼至地球中心连线与地面的交点，定义X轴指向水平正东方向，Y轴指向水平正北方向，Z轴垂直于XOY平面，指向天空，即与重力方向相反。

机体坐标系定义如下：由于四旋翼在形状上关于中心对称，因此四条机臂是等价的。选取Xb轴指向其中一条机臂的方向，Yb轴指向逆时针转过90°，与Xb轴垂直的另一条机臂的方向，Zb轴垂直于XOY平面，指向四旋翼飞行器上方。

为确定四旋翼姿态，分别定义欧拉角如下。

●滚转角φ：在YOZ平面的投影与OY的夹角

●俯仰角θ：在XOZ平面的投影与OZ的夹角

●偏航角ψ：在XOY 平面的投影与OX的夹角

从机体坐标系变换至地面坐标系的转换矩阵记作Rg/b，需要经过三次欧拉旋转获得（许喆.四旋翼无人机控制系统的设计与实现[D].南京:南京理工大学,2017）：

首先，绕Zb转动ψ角，变换至中间坐标系A，此变换矩阵记作RA/b。

之后，绕转动θ角，变换至中间坐标系B，此变换矩阵记作RB/A。

最后，绕转动φ角，变换至地面坐标系，此变换矩阵记作Rg/B。

可得由机体坐标系变换至地面坐标系的转换矩阵Rg/b。

最终得到Rg/b。

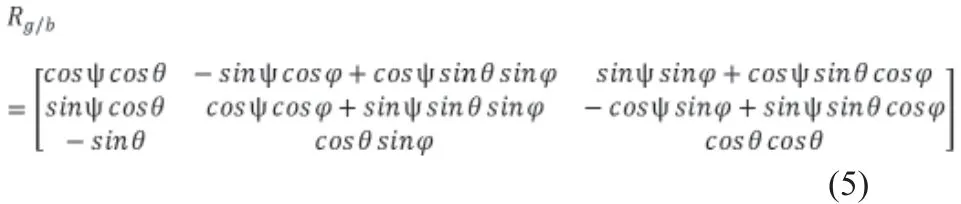
2.2 四旋翼动力学建模

记四个旋翼的转速分别为～，这也是实际的输入的控制量。单个旋翼沿轴正方向的拉力可近似认为与该旋翼转速的平方成正比（米培良.四旋翼飞行器控制与实现[D].大连:大连理工大学,2015）。

其中，f 为升力系数。

容易写出四旋翼在地面坐标系下受到的合力。

同理，可以写出机体坐标系下三个力矩平衡方程（冯培晏.四旋翼无人机建模与PID控制器设计[J].工业设计,2018(6):135-137）。

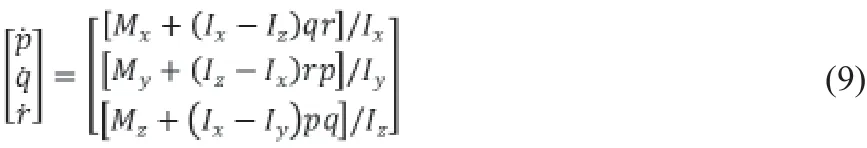
其中，l为四旋翼机臂长，d为电机反扭矩系数。

可以写出机体坐标系下各轴角速度与四旋翼滚转、俯仰、偏航角速度之间的关系。

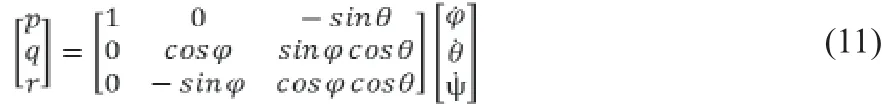
根据前文假设，本文研究的情况为四旋翼无人机小角度、低速度飞行，因此可以做如下近似。

即：

通过对进行变换，令：

可得四旋翼飞行器最终模型。

3.四旋翼仿真与控制率设计

3.1 四旋翼模型仿真

根据查阅的文献（李俊,李运堂.四旋翼飞行器的动力学建模及PID控制[J].辽宁工程技术大学学报(自然科学版),2012,31(1):114-117），得到四旋翼模型参数如表1所示。

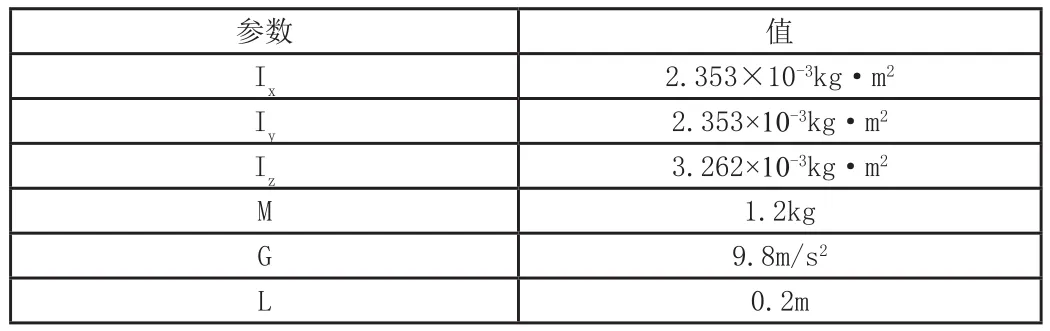
表1 四旋翼模型参数

四旋翼仿真使用Matlab/Simulink完成。仿真模型代码如下：

其中，使用rand()函数，生成0～1之间的随机数，以模拟四旋翼受到的扰动。

3.2 四旋翼控制率设计

由四旋翼模型可以看出，其模型有四个输入变量与六个输出变量，属于不完全控制，各变量之间相互之间存在耦合。

在设计控制率时，首先对模型进行化简。由于本文假设四旋翼是在小角度、低速度的情况下进行飞行，因此可以忽略陀螺效应对三轴角速度带来的影响（米培良.四旋翼飞行器控制与实现[D].大连:大连理工大学,2015）。从而得到化简后的模型。

观察化简后的四旋翼模型，可以发现其三个姿态角变量以及高度变量仅与四个输入变量有关，而X、Y轴位置的控制则同时与输入以及姿态角有关（米培良.四旋翼飞行器控制与实现[D].大连:大连理工大学,2015）。四旋翼飞行器的姿态与高度均完全可控。因此，将四旋翼模型拆分成两个子控制系统，内环系统为姿态控制系统，外环系统为位置控制系统。

图4 姿态角控制系统与位置控制系统

系统使用PID控制率进行控制。PID是P（比例）算法与I（积分）算法与D（微分）算法三种算法各种组合的统称。可以选择为PD，PI，单独的P算法等。P（比例）以减少系统稳定性为前提减小系统误差。I（积分）和D（微分）必须和P（比例）控制搭配使用，I（积分）反映系统的累计偏差，使系统消除稳态误差。D（微分）反映系统偏差信号的变化率，具有预见性，从而进行超前控制（冯培晏.四旋翼无人机建模与PID控制器设计[J].工业设计,2018(6):135-137）。

图5 四旋翼控制系统仿真

从系统仿真框图中可以明显看出位置与姿态两个相对独立的字系统。X、Y位置指令首先输入外环控制系统，即位置控制系统，其输出作为内环控制系统，即姿态控制系统的输入控制四旋翼的滚转角与俯仰角。采用先调节内环，后调节外环的策略，调节系统各个PID的参数。最终结果如表2所示。

表2 四旋翼PID控制参数

3.3 四旋翼控制率验证

对控制系统进行测试，令四旋翼在1米的高度按照半径为2的圆轨迹进行飞行，输入如下控制指令。

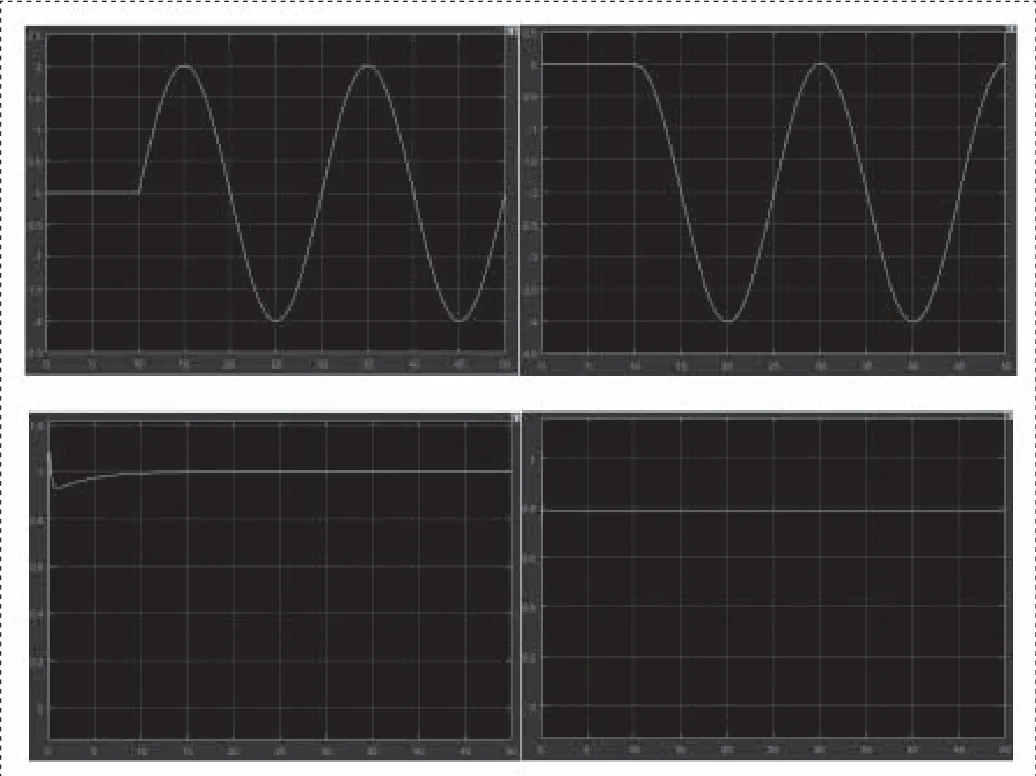
图7 X、Y、Z与φ控制结果仿真

从结果可以看出，PID控制系统对于四旋翼飞行器有较好的控制效果，飞行器可以在具有扰动的情况下，根据指令按照设计的轨迹进行飞行。

4.结语

本文首先对四旋翼飞行器进行了简介，之后对四旋翼进行了建模，并对模型进行了简化，得到了适合控制使用的四旋翼动力学模型。根据得到的模型，本文对该模型进行了仿真，并设计了PID控制率，使得飞行器能够按照指令沿一定轨迹进行飞行，并验证了控制率的正确性。

然而，本文的模型与控制率设计仍然存在不足。对比真实的四旋翼模型，本文的模型过于简单，并没有考虑到许多实际中可能出现的影响因素，如空气阻力等。同时，本文的PID控制率也不适用于在复杂的实际条件下进行飞行。未来的工作将会重点集中于对四旋翼进行精确建模，并采取更加先进的控制方法以实现对四旋翼飞行更好的控制效果。