松花江流域省界缓冲区水质监测指标优化
郑国臣,官 涤,崔 迪,姜厚竹
(1.松辽流域水资源保护局,吉林长春130021;2.哈尔滨工程大学航建学院土木与环境工程系,黑龙江哈尔滨150001;3.哈尔滨商业大学生命科学与环境科学研究中心,黑龙江哈尔滨150076;4.东北林业大学林学院,黑龙江哈尔滨150040)
1 序言
为了准确认识松花江流域省界缓冲区的水环境问题,在确定监测指标范围、指标种类、监测指标水质标准时,对水质监测工作中要求的必测指标进行全面长期监测,根据相关的监测数据对水质监测指标进行优化。《地表水环境质量标准》(GB3838-2002)中规定的监测水质指标有温度、浊度、pH、溶解氧、高锰酸盐指数、化学需氧量(COD)、总磷等共109项。若在水质监测时将所有的指标都进行测定,则会增大工作量,同时也会降低主要污染物对环境的主导作用。因此,有必要对标准中规定的监测指标进行优化筛选,最终确定的监测指标必须可以全面的、较为准确的反映松花江流域省界缓冲区的水质特征。在对指标进行优化筛选时须将流域缓冲区内的主要的污染物、超标污染物、随时空变化而变化较大的污染物等污染特征等因素考虑进去:如COD、氨氮是造成水质恶化的重要污染物,国家将这两项列为国家重点监控的污染物,因此,水体中COD、氨氮是水质监测的必测项目,使监测结果满足全面性、准确性、科学性,为明确水环境质量现状和变化趋势提供数据支持。
2 软件及其研究方法
2.1 SPSS软件
SPSS23.0软件的编程步骤键位简单,具有完美的图形处理能力,运用类似的表格方式输入与管理数据,强大的数据对接功能,能方便的从其他数据库读入数据。用二维图和感知图来清晰地更完整方便的分析出数据中的关系,通过类似传统的回归分析、主成份分析及典型相关分析的分析方法,处理分类数据及定序数据[1]。
考虑松花江省界缓冲区主要的污染源为生活污水、工业废水和动植物腐烂分解后随降雨流入水体、农用化肥的流失及雨水径流[2];主要污染途径分别为生活污水、工业废水与径流补给这三类。经过简单的筛选后得到13项常规理化指标因子,文中选用2015年松花江流域省界缓冲区51个监测断面的13项常规理化指标因子(pH值、溶解氧、高锰酸盐指数、化学需氧量、五日生化需氧量、氨氮、总磷、铜、锌、氟化物、硒、砷、粪大肠菌群)的监测数据作为元数据,利用SPSS 23.0软件对水体监测指标进行主成分分析,得到维度较少的几个因子,从而实现对水质监测指标进行优化[3]。
3 水质监测指标优化过程分析
3.1 监测数据标准化处理
数据的标准化处理过程是将同一指标的监测数据减去其均值后,所得结果除以该组监测数据的标准差。用SPSS软件分析后得出的原始变量的描述性结果输出如表1所示,该表中包含原始变量的统计结果,包括平均值、标准差和分析样本个数。从表1中可以看出我们所选的51个监测断面中pH值、溶解氧、高锰酸盐指数等13个水质指标的监测数据结果。
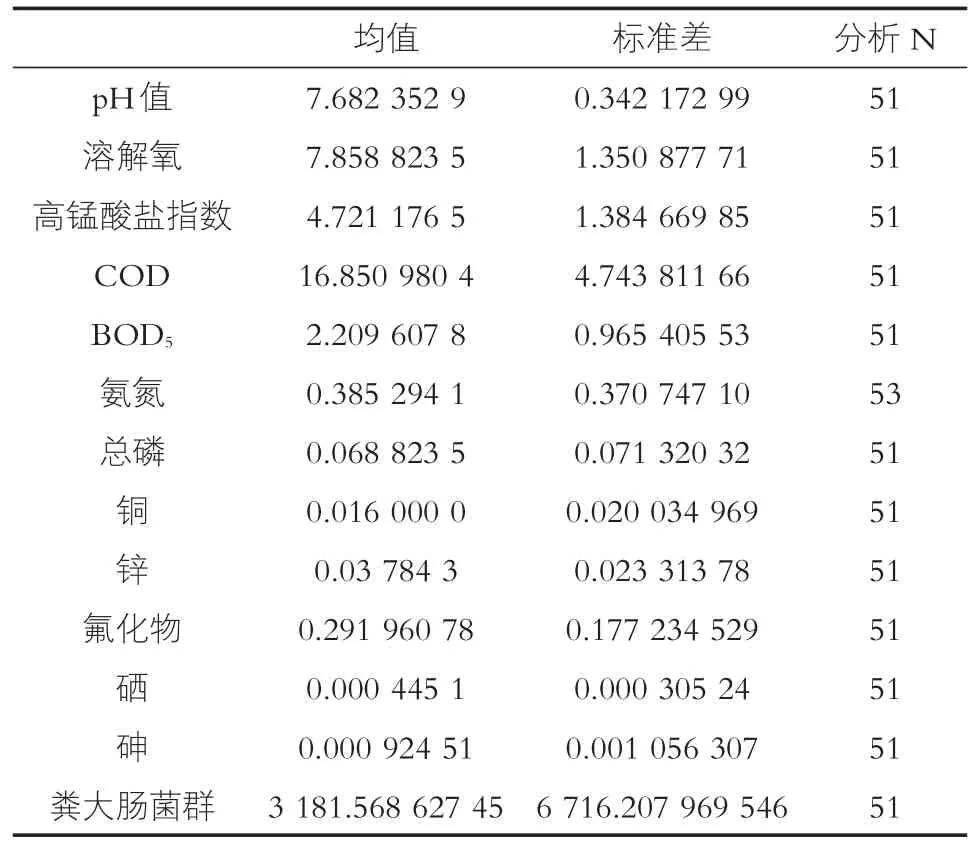
表1 描述统计量

表2 相关系数矩阵
从表2相关系数矩阵中可以看出,大部分相关系数几乎均大于0.3,表明上述数据中各变量之间存在着的较强的直接相关性,这证明各指标之间所传达的信息具有一定的重叠,这一结果表明这些原始变量比较适合做因子分析。
3.2 检验是否符合主成分分析条件
在用SPSS做主成分分析时,通常需要对所收集的数据做KMO检验和Bartlett’s球型检验来判断元数据是否符合主成分分析条件。KMO统计量是通过比较各变量间简单相关系数和偏相关系数的大小来判断变量间的相关性,取值范围在0和1之间。Kaiser给出了常用的KMO度量标准:一般情况下,KMO越接近1,意味着变量间的相关性越强,表明该组数据越适合做主成分分析,当KMO<0.5时,则不适合做主成分分析。
Bartlett’s球型检验(巴特利球形检验)是用于检验相关阵是否是单位阵,即各变量是否独立,以变量的相关系数矩阵为出发点做出零假设:相关系数矩阵是一个单位阵。如果巴特利球形检验的统计计量数值较大,且对应的相伴概率值小于用户给定的显著性水平,则应该拒绝零假设;反之,则不能拒绝零假设,认为相关系数矩阵可能是一个单位阵,不适合做因子分析。若假设不能被否定,则说明这些变量间可能各自独立提供一些信息,缺少公因子,适合做主成分分析[4]。

表3 KMO和Bartlett的检验
从表3的主成分分析结果可以看出,KMO测量值为0.660,明显大于0.500,表明该组数据适合做因子分析。Bartlett的球形检验的显著性为0.000,小于0.050,即拒绝原假设相关系数矩阵为单位矩阵,说明变量之间存在着相关性,同样表明该组数据适合进行因子分析。
3.3 特征根及方差贡献
特征值大小表征矩阵正交化之后所对应特征向量对于整个矩阵的贡献程度,在某种程度上可以理解为主成分影响力度大小的指标,若特征值小于1,说明该主成分的解释力度还不如直接引入原变量的平均解释力度大,因此,一般可以用特征值大于1作为纳入标准。累积贡献率,即因子对原始变量的解释程度。由表4可知,通过主成分分析法提取了四个主要成分,即m=4。其中第一主成分的贡献率为27.330%,第二主成分的贡献率为18.945%,第三主成分的贡献率为18.944,第四主成分的贡献率为11.344,第1到第4个主成分的累计方差贡献率达到了76.563%,表明这4个主成分可完全代替原13项指标。
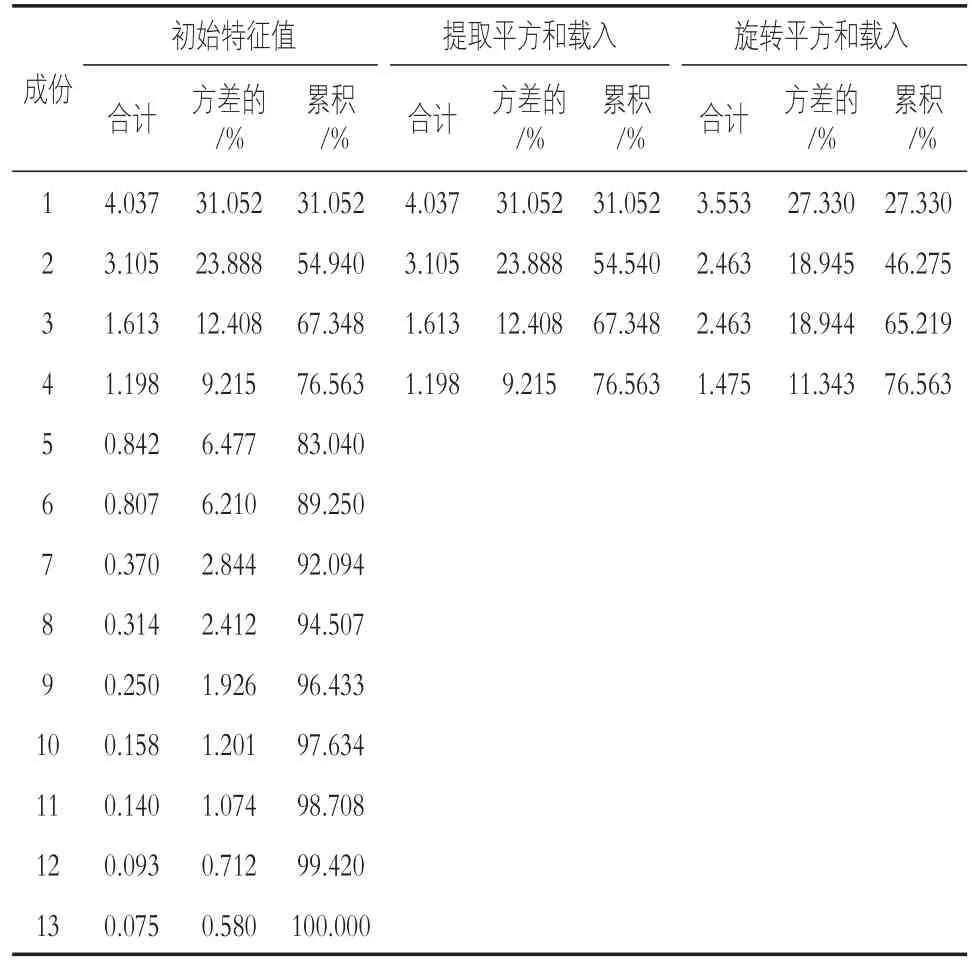
表4 解释的总方差
3.4 主成分负荷及主成分得分
表5是最终的因子载荷矩阵。
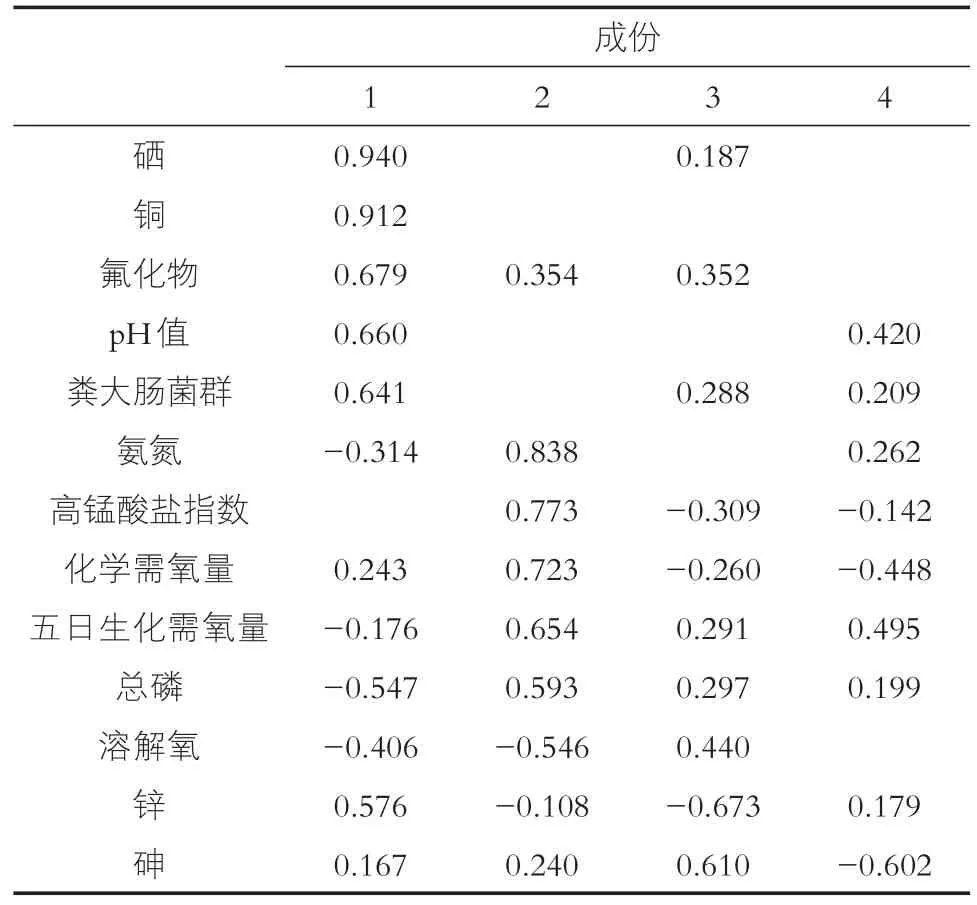
表5 成份矩阵a
按照前面设定的方差极大法对因子载荷矩阵旋转后的结果如表6所示。主成分载荷矩阵每一列载荷值都显示了各个变量与有关主成分的相关系数相关系数的绝对值越接近1,表明该成分越具有代表主成分的性质。未经过旋转的载荷矩阵中,因子变量在许多变量上都有较高的载荷。经过旋转之后,可以看出第一主成分上铜、硒载荷较大,即与第一主成分的相关系数高,第二主成分上只有COD在占有较高的载荷,而在第三主成分上,BOD5、氨氮和总磷三个指标所占的载荷较高,第四主要成分同样也只有一个指标,砷,所占的载荷较大,因此,砷同样作为第四主成分来反映水质情况。为了实现水质监测指标的优化,可以考虑用铜、硒、COD、BOD5、氨氮、TP和砷7项水质监测指标来代表原来的13项水质指标。
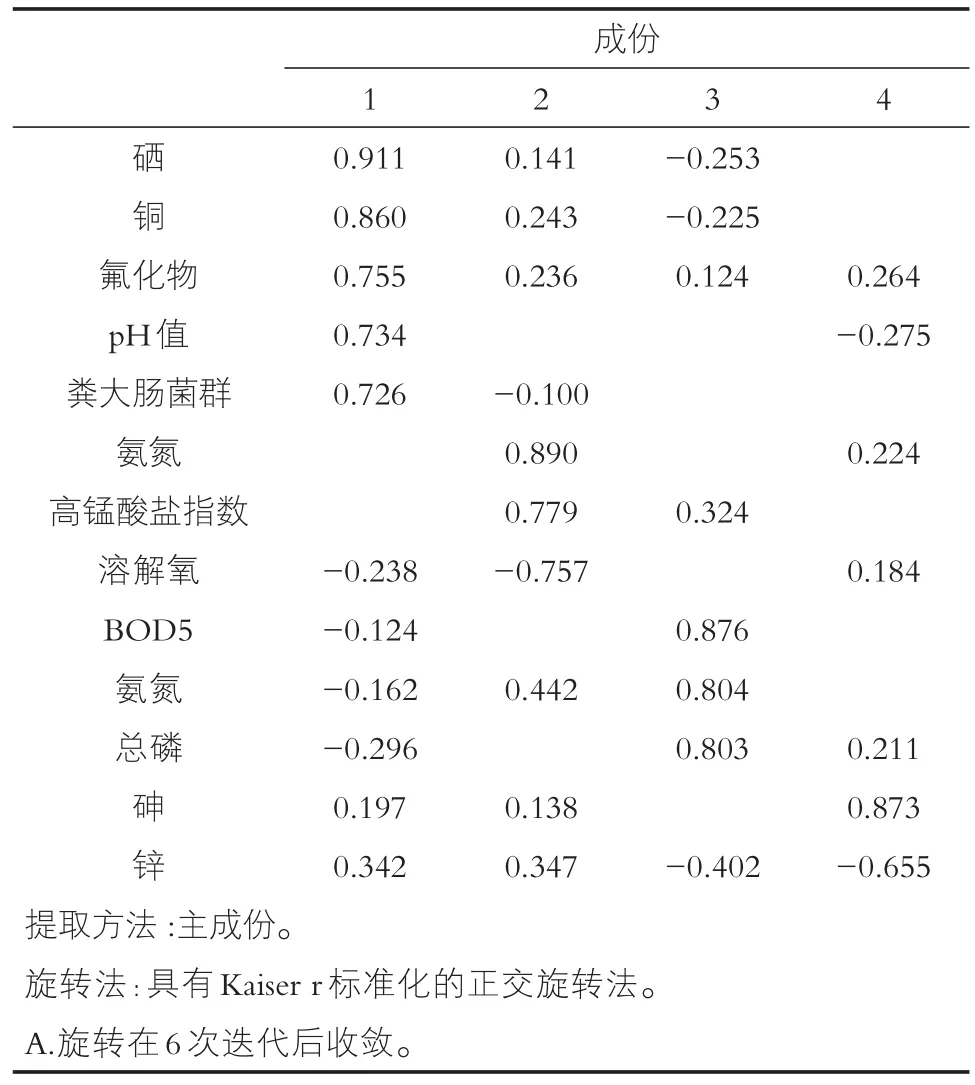
表6 旋转成份矩阵a
4 结语
对2015年松花江省界缓冲区水质监测数据分析,将监测指标划分为必测项目、优化频率必测项目和选测项目等类型,经过简单筛选选出13项常规理化指标(pH值、溶解氧、高锰酸盐指数、化学需氧量、五日生化需氧量、氨氮、总磷、铜、锌、氟化物、硒、砷、粪大肠菌群),以上述指标监测值作为元数据,利用主成分分析法,借助SPSS 23.0软件来对水质指标进行进一步筛选,通过计算和模拟,确定松花江流域省界缓冲区的可以考虑用铜、硒、化学需氧量、五日生化需氧量、氨氮、总磷和砷等7项指标来代表该流域水质状况,从而实现对松花江流域省界缓冲区水质监测指标的优化。

