基于改进图论与水文模拟方法的河网水系连通性评价模型

高玉琴，汤宇强，肖 璇，陈鸿玉，刘云萍，周 桐

(河海大学水利水电学院，江苏 南京 210098)

水系连通是河流生态保护与修复以及河流健康评价的重要指标，畅通的河网水系能够改善流域应对环境变化的能力，实现水资源的高效配置，是流域防洪抗旱、保障供水及水生态安全的重要基础[1]。近年来，国内外学者逐步开始了对水系连通概念及其评价方法的研究。徐慧等[2]将河流廊道理论和景观生态学方法应用于太仓市水系规划前后水系连通度的对比分析中，用以验证城市水系规划的效果；Lane等[3]通过构建CURM2D水文模型，提出了可以用流域湿度分布来评价水系的景观水文连通性；Cui等[4]基于图论中的最短路径算法对低流量和高流量两种情况下的河网结构进行了优化；Karim等[5]通过MIKE21构建了水动力学模型来量化湿地与河流之间的连通程度；孟慧芳[6]基于水流运动阻力与水文连通性，提出河流连通性计算模型，反映了河网水系的自然和社会属性对河流连通的影响；窦明等[7]构建了描述水系连通形态和连通功能的两套指标体系，定量分析了二者之间的相关性，进一步探究了水系连通形态的变化对连通功能的影响。

目前的水系连通模型多数仅对水系结构进行分析，忽视水流的运动状态[8-10]；或基于水力学的评价方法，所需数据量大且不易获得，计算步骤烦琐[11-12]。因此有必要完善现有水系连通评价方法，综合考虑影响水系连通程度的多方面、多层次因素。本文在文献[13]的基础上进一步改进评价方法，基于改进图论算法与水文模拟方法，计算连通因子w，以w表征河道的动态输水能力，实现对流域水系的动态输水连通与静态结构连通的综合评价。

1 评价模型的建立

基于水文模拟得到的河道径流量q计算连通因子w，以其作为边的权值得到加权邻接矩阵B，进而计算出判断矩阵T，将该判断矩阵中的各元素与传统图论得到的判断矩阵S中的各元素相除得到各顶点平均连通度uij，取均值作为水系整体连通度U。为使评价结果更具有可比性，进一步提出连通水平的概念，以更加直观地了解流域水系连通程度。

表1 防洪保护区的防洪等级和防洪标准

1.1 水量传输能力指标选取

可以表征水量传输能力的指标有年平均径流保证率、河道流量、河道水位、平均流速等[14]，这些指标从多角度反映了河网水系的水量传输能力。基于流动性和连续性两个角度对指标进行优选，用河道流量作为评价指标时，其值大于零表示水流连续，且值越大流动性越好，因此河道流量既能表征连续性也能表征流动性，是水量传输能力最直观的表征参数。此外，水系连通的目的是实现特定的服务功能，包括防洪、供水、排污、通航等，而这些功能均要求河网具有较大的流量，以达到强化洪涝外排能力、增大供水量、促进以清释污等效果，因此选用河道流量作为水量传输能力指标[15]。

1.2 模拟流量基准选取

河道流量采用水文模型HEC_HMS模拟得到，该模型通过划分子流域的方式充分考察流域下垫面的区域性差异，各子流域独立设置参数并进行径流模拟，然后再以子流域为单位进行产汇流演算得到流域出口的径流过程[16]，充分考虑了地形、土壤含水率、土壤类别以及土地利用方式等因素对径流模拟的影响，模拟结果符合实际情况，合理可信。

通过对数场降雨进行模拟，得到河网各节点处的峰值流量，运用上述方法计算连通度，发现大部分数值偏小且集中分布在较小范围内，无法较好地基于连通水平对连通程度进行分级。此外，为充分发挥河道潜在的排涝、排污能力，需要尽可能提高设计降雨标准以检验河道最大过流能力，但需要满足区域内防洪要求，因此在模拟河网产汇流过程时，选用满足一定防洪标准的典型设计降雨过程作为模型输入，将得到的峰值流量作为水系连通评价的流量基准。城市与乡村防护区的防洪等级和标准如表1所示。

综合考虑城市和农村地区的防洪要求，选取重现期为50年一遇的设计洪水作为防洪标准，可满足一般城市和重要乡村的防洪需求。假定设计洪水与设计暴雨同频率，本文采用适线法绘制经验频率曲线，并用同倍比放大法计算经验频率为2%的设计降雨过程。

1.3 连通度计算

1.3.1 基于水文模拟方法的连通因子计算

将HEC_HMS模型模拟得到的河网各节点处的峰值流量作为水量传输能力指标值。通过大量实例运算，发现若直接将流量值替换邻接矩阵中的元素，会由于邻接矩阵本身包含的数据量巨大，且含有大量乘方运算，导致程序运行缓慢、容易超出计算能力而报错，因此，进一步构造连通度因子wij∈(0,1)，用该连通度因子来表征连通程度的好坏，计算公式为

(1)

式中qi为顶点i处河道峰值流量，m3/s。当qi=0时，wij=0，表示顶点i与顶点j完全不连通；当qi→+时，wij=1，表示顶点i与顶点j完全连通；qi越大则wij越接近于1。

1.3.2 流域平均连通度计算

将连通度因子wij替换邻接矩阵中的元素，得到改进后的邻接矩阵Bn×n=(bij)n×n，则判断矩阵

任意两河流节点间的连通度为

(2)

式中：n为节点数；tij为顶点i和顶点j之间连接长度为1、2、…、n-1的所有路径的连通度因子之和；sij为顶点i和顶点j之间连接长度为1、2、…、n-1的所有路径的总数，sij≠0。

节点间连通度uij可以衡量流域中任意两河流节点间的连通性，对流域整体来说，对所有节点间连通度求均值可得到流域平均连通度U：

(3)

1.3.3 连通水平计算

为使评价结果更具有可比性，本文提出连通水平的概念。将研究区历史最大降雨过程作为HEC_HMS模型输入，得到历史最大连通度，以该值作为标准连通度Us，则水系连通水平L可表示为

(4)

综上，基于改进图论与水文模拟方法的河网水系连通评价模型的主要特点有：

a. 综合考虑城市和农村地区的防洪要求，选取一定重现期下的设计洪水作为防洪标准，推求相应设计降雨作为模型输入。

b. 将表征水量传输能力的指标——河道流量q，转化为邻接矩阵中的元素，使邻接矩阵不仅能反映河网节点间是否连通，还能反映连接通道的过流能力。

c. 进一步提出了连通水平的概念及计算方法，可直观反映出区域在某段时间内的连通程度。

2 实例验证

2.1 秦淮河流域概况

秦淮河流域位于长江下游江苏省境内，流域面积2 631 km2，地势由东南向西北倾斜。流域地处亚热带湿润、半湿润季风气候区，四季分明，降水丰沛，汛期在5—9月，平均降雨量为652 mm，占年均降水量的63%。秦淮河全长110 km，干支流纵横交错，有溧水河、句容河两源，两源在江宁县西北村汇为秦淮河干流，流至江宁区东山街道又分为两支：北支为主河道，过市区后于三汊河口入长江；西支为秦淮新河，经西善桥至金胜村入长江[17]。

2.2 数据处理

2.2.1 数字水系图获取

分别选取2000年和2010年的高程数据，基于ArcGIS软件中水文分析工具箱，对数据执行填洼、流向、流量、栅格计算器、栅格河网矢量化等命令，提取数字河流网络，并对照Google Earth影像图进行适当修正，进一步概化为包含40个顶点的拓扑结构图。图1为秦淮河流域数字水系，图2为2010年研究区拓扑结构。

(a)2000年

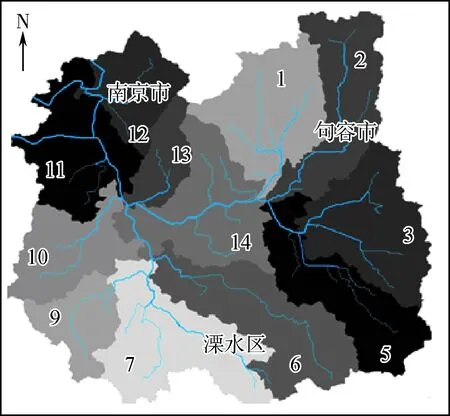
(b)2010年

图2 2010年秦淮河流域拓扑结构

2.2.2 洪水过程模拟

a. HEC_HMS模型率定与验证。对HEC_HMS模型构建过程中使用的大量估算参数进行率定与验证[18]，秦淮河流域HEC_HMS模型模拟评价指标如表2所示。由表2可见，率定期3场洪水的洪量及洪峰相对误差均在20%以内，Nash系数及相关系数均大于0.7；验证期4场洪水的洪量及洪峰相对误差基本控制在20%以内，Nash系数及相关系数均大于0.7，模拟值与实测值吻合较好，模拟的峰值流量可用于评价模型的计算。

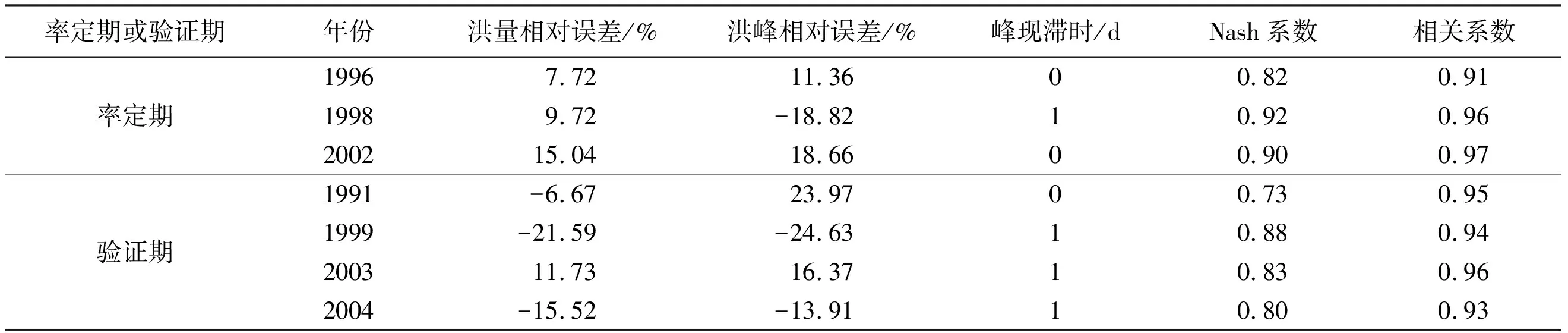
表2 秦淮河流域HEC_HMS模型模拟评价指标

表3 秦淮河流域2000年和2010年水系结构指标

b. 2000年和2010年洪水过程模拟。对秦淮河流域武定门闸1986—2006年年最大降雨量进行排序，选用皮尔逊Ⅲ型曲线进行水文频率计算，采用矩法计算曲线参数，得到

通过查询皮尔逊Ⅲ型曲线离均系数ψ值表，可计算得到P=2%时的设计降雨量为618.08 mm。选择洪峰流量最大的198606次洪水作为最不利降雨过程，采用同倍比放大法得到50年一遇设计降雨过程。将放大后的降雨过程导入HEC_HMS模型，即可模拟全流域相应的流量过程，以其峰值流量作为该水文要素的水量传输能力指标值。

2.2.3 连通度及连通水平计算

由图论连通度计算可得，2000年和2010年秦淮河流域河网水系连通度均为2。由此可见，仅使用图论对秦淮河流域进行水系连通评价时，结论为流域水系连通水平在10年间无显著变化，这显然不符合实际情况。运用本文提出的评价模型计算，秦淮河流域水系2010年连通度U2010=0.002 9，该值代表了流域在满足防洪要求下的连通状态。根据秦淮河流域内有观测记录以来的降雨资料，最大降雨过程发生在2007年7月，总降雨量为729.2 mm，以该历史最大降雨过程作为HEC_HMS模型输入，可求得标准连通度Us=0.005 3，则L2010=54.7%。采用同样的方法，可得U2000=0.004 4，L2000=83.0%。

2.3 结果分析

表3为秦淮河流域2000年和2010年水系结构指标统计，可以看出，从2000—2010年秦淮河流域水系的河流长度、河网密度以及水面率均呈缩减趋势，水系连通性变差。基于本文提出的评价模型的计算结果可知，秦淮河流域水系连通度由2000年的0.004 4下降至2010年0.002 9，水系连通水平由83.0%下降至54.7%，2010年水系连通度处于较低水平，这与水系结构指标变化情况一致，说明本文提出的评价模型是合理、可靠的。

秦淮河流域2000年和2010年水系连通性变差的原因，可能与该期间秦淮河流域内以南京为代表的城市群加速推进城市化进程有关，剧烈的人类活动导致流域不透水面积增加，部分天然河道萎缩甚至消失，土地覆被退化，区域防洪、供水与生态安全受到严重威胁，流域连通水平受到极大影响。

3 结 语

进入21世纪以来，图论方法被国内学者不断应用于水系连通评价领域，本文模型利用水文模型模拟出的峰值流量对边赋权值，将河网结构特性与河道实际水文特性相结合，避免了用传统图论方法进行水系连通评价过程中出现的“连”却不“通”的现象，使评价结果更符合实际情况。较目前流行的水流阻力与图论相结合的评价方法而言，本文模型计算过程简单，数据易获取，有较大的推广意义。

本文对水系连通评价方法进行了探索与研究，但仍存在不足，未将该方法与水资源调配、洪旱灾害、水生态环境等实际问题相联系，因此，可进一步进行水系连通性与可调配水量、洪涝风险因子、水质变化规律的相关性分析，验证评价模型的准确性。此外，2000—2010年期间水系连通性是否一直呈现下降趋势，还有待进一步分析研究。