道路养护作业区交通延误分析

黄旭成

(广西翔路建设有限责任公司，广西 南宁 530029)

0 引言

近年来我国道路交通事业迅速发展，随着运营时间的推移，我国将面临道路养护维修任务繁重的局面。道路养护维修工作必然会对城市道路和高速公路的正常运行带来干扰，甚至带来危害。道路养护作业区必然会对交通流产生一些影响，比如：车辆延误、交通拥挤等。在道路作业区存在的情况下，车辆延误费用激增[1]。

因此，开展养护作业区交通延误研究，对于减少道路使用者出行费用、养护作业区布置及其交通管理具有重要的作用和价值。国内外很多学者对道路养护作业区进行了比较系统的研究，并取得一定的研究成果[2-5]。

以往对于道路养护作业区的研究，基本都是对于整个养护作业区的，鲜有对上游过渡区的研究。因此，该文利用Vissim软件从限速与上游过渡区这两个方面来研究，并分析了其两者的关系。

1 上游过渡区延误分析

道路养护作业区共分为警告区、上游过渡区、缓冲区、工作区、下游过渡区、终止区等6个部分[6]。在本文中，用S、Ls、H、G、Lx、Z等6个字符分别代表警告区、上游过渡区、缓冲区、工作区、下游过渡区、终止区的长度数值大小(不含单位)，各区的长度单位均为米。双向四车道道路养护作业区示意图如图1所示。两条车道的车流在上游过渡区汇集，封闭车道的车辆在上游过渡区驶入原正常车道时会形成一个中断区域，到达这个区域的车辆会受到阻滞，产生延误(主要包括运行、排队、减速延误[7])，从而使交通延误增加，路段阻抗上升，服务水平降低。由于造成车辆延误的影响因素很多[8]，而交通仿真[9]技术能模拟不同车辆在不同的管理条件下的运行状况，因此将其用来分析上游过渡区交通延误。

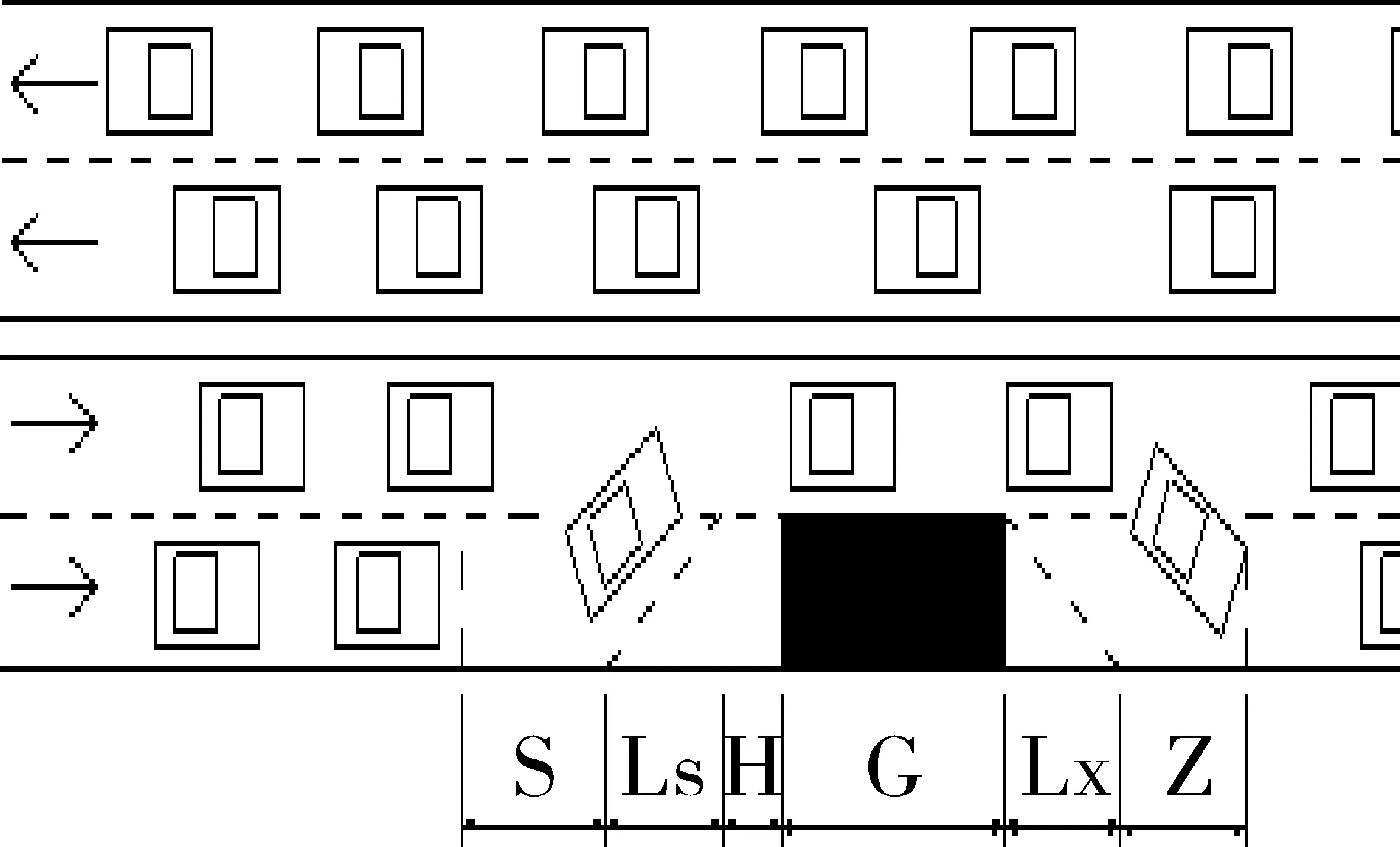
图1 双向四车道关闭1条车道道路养护作业区示意图

2 交通仿真技术分析上游过渡区车辆延误

2.1 Vissim交通仿真软件简介

本文采用德国PTV公司开发的微观交通流仿真软件Vissim作为分析工具，它是一个基于时间的、时间离散的、随机的微观模型，以驾驶员—车辆—单元为基本实体，采用生理—心理跟车模型(Wiedemann 1974)[10]。Vissim软件能提供行程时间、延误、排队长度及停车次数等多项指标来评价交通过程，而且较解析法建立的延误模型更贴近于实际[11]，更加详实准确。

2.2 研究方法

该文采用图1所示模型，假设条件：

(1)到达上游过渡区上游的交通量q/(pcu/h)给定，且各条车道的车辆比例为1∶1；每条车道的宽度均为3.75 m，其中q仅代表交通量的数值大小(不含单位)，交通量的单位为pcu/h。

(2)模型中忽略不同类型车辆带来的影响，并将各种车型换为标准车型小客车[12]。

选取限速v/(km/h)，相对应的Ls/(m)分别为0.5v、v、1.5v、2v，其中v仅代表限速的数值大小(不含单位)，限速的单位为km/h。分别取q为1 000、2 000、3 000，v为20、40、60。记录时间从600 s～3 600 s，每个600 s出一次数据。其他参数均选取Vissim软件默认参数。结果见表1，行程时间、延误、停车次数、平均排队长度的数值大小用T、D、C、A来表示(其中T、D、C、A仅代表数值大小(不含单位)，其相对应的单位分别为s、s、次、m。

3 仿真结果与分析

表1 q=1 000时不同v与Ls的交通延误指标表

表3 q=3 000时不同v与Ls的交通延误指标表

由表1～3中的数据可知，v、q在一定范围以内，随着上游过渡区长度Ls的增大，行程时间T也随着增大。

(1)v=20

当Ls=0.5v、q为1 000、2 000、3 000时，没有延误，但C、A都较大，且相差不大，很可能是因为过渡区长度短，速度相对较慢，因此造成冲突较多，导致停车次数较多，平均排队长度较长。当q=1 000、Ls为v、1.5v、2v时，出现了延误，但C、A都为0，很明显，在速度一定的情况下，随着Ls的增大，车辆汇集到一条车道的空间也随着增大，冲突减少，车辆在过渡区已不需要停车与排队等候，之所以会出现延误，是因为受到车速的制约。当Ls为v、2v时，q=2 000相对当q=1 000的情况，延误分别增加了0.5 s、0.1 s。

可见，当v、Ls长度一定，随着车流量的增大，延误也会随之增大；当Ls=1.5v，q为2 000、3 000时，D均为0，很明显，在Ls=v与Ls=2v之间，会存在一个或者多个使延误为0的Ls值。假设Ls=1.5v，q为1 000、2 000、3 000时的T分别为4.4、4.5、4.9，相对行程时间均为1.7 s的Ls=v的情况，波动起伏较大，而且在同样没有延误的情况下，可以认为在v=20的情况下，Ls至少可以取为0.5v。

(2)v=40

当q=1 000时，随着Ls的增大，车辆不存在延误，很明显就是交通量过少的原因造成的。当q=2 000时，其与q=1 000的情况差不多，但当Ls=20时，出现了交通延误。行程时间为1.9 s，延误为0.1 s，很明显，若不存在交通延误则会与q=1 000的情况一致。可见，当Ls一定，随着车流量的增大，延误也会随着出现。当q=3 000时，Ls=0.5v、Ls=v的D、C、A分别为0.9、0.4、53；22、8、6，相对q=2 000的情况出现了很比较大的延误，可见，当Ls长度一定，随着车流量的增大，停车次数、平均排队长度、延误也会随着增大，同时q=3 000时，Ls=1.5v、Ls=2v的C、A均为0，可见，随着Ls长度的增大，停车次数与平均排队长度也会随着减少。

很明显，在Ls=v增加到Ls=1.5v时，在q为2 000、3 000相同的情况下，交通延误已经消失。而且，考虑到q为2 000、3 000，Ls=v时，T为3.5、3.7，Ls=60时，T均为5.3，两者的行程时间之差相隔1.8、1.6，因此选择Ls至少为40 m，即v。

(3)v=60

当q=1 000时，只有Ls=0.5v时出现延误，且D为0.3 s，很明显就是上游过渡区长度太短的原因造成的。随着Ls长度增大，车辆不存在交通延误，是因为车速比较快，而且车流量过少。

当q为2 000、3 000时，其与q=1 000的情况差不多。但是Ls=2v时，出现了0.1 s的交通延误，很明显，这是由于交通量的增大造成的，若不存在交通延误则会与q=1 000的情况一致。

很明显，在速度一定即60 km/h，车流量在一定范围内增大时，Ls为1v、1.5v时不出现延误。但是60 km/h的速度相对较快，万一遇到突发情况，需要及时刹车，再加上人体的反应延迟时间，会使车辆在停止运动之前再前进一段距离。因此，Ls的大小可以选取为1.5v。

4 结语

本文利用Vissim软件从限速与上游过渡区这两个方面来研究道路养护作业区交通延误，并分析其两者的关系，得出了限速为20 km/h、40 km/h、60 km/h时相对应的上游过渡区长度为10 m、40 m、90 m，验证了公路养护安全作业规程中规定的上游过渡区最小的长度，同时也可为决策部门提供理论和技术参考。