基于双剪强度理论的岩溶隧道掌子面防突厚度分析
何升锋
(广西浦信高速公路有限公司,广西 南宁 530000)
0引 言
我国地域辽阔,岩溶地貌分布广泛,约占国土总面积的11%,尤其在西部地区,岩溶地貌分布更加集中。随着我国西部大开发的不断进行,岩溶地貌给工程建设带来的问题不断涌现,比如:基础下的岩溶问题、路基下的岩溶问题、隧道建设中的岩溶问题等。本文针对岩溶隧道中富水溶腔对掌子面造成的突水问题进行探讨。
近些年随着我国交通基础设施的大力发展,尤其在山区,经常会遇到需要开挖隧道的情况。在岩溶地区,由于地下水的溶蚀作用,很容易形成具有高压富水溶腔。在隧道开挖的过程中,当遇到前方分布有高压富水溶腔的情况时,很容易造成掌子面突水及隧道的垮塌、人员伤亡等工程事故。因此,合理地解决岩溶区隧道掌子面的防突水问题,具有重要的工程和经济意义。
目前,针对岩溶区隧道掌子面的防突水问题,已有很多学者对此进行了研究。郭佳奇等基于厚板理论对岩溶区隧道掌子面的防突厚度进行了分析,并给出了在固支和简支两种模型下的防突厚度的计算;杨子汉等基于上限稳定理论和Hoek-Brown准则对隧道环向隐伏富水溶洞防突厚度进行了分析;刘超群等采用数值分析软件建立相应的掌子面防突岩墙的模型,对掌子面防突厚度进行了分析并与理论计算结果进行了对比。本文在前人研究的基础上,引入双剪强度理论与极限分析上限法相结合,进一步考虑中间主应力对掌子面防突厚度的影响。
1 双剪强度理论
1.1 轴对称问题的屈服条件
俞茂宏在1961年提出了双剪强度理论。它可以充分考虑单元体在双剪应力作用下,所有的应力分量对材料的影响,并且还可以考虑岩体在受力屈服条件下的塑性,对于求解岩体等材料的抗冲切问题极为适用。对于轴对称问题,双剪强度理论的具体表述如下:
设岩体的抗压强度为σc,抗拉强度为σt。并令:
(1)
(2)
式中,α<1,m>1。
由双剪强度理论可知,岩体屈服破坏的条件为:

(3)
式中,σ1为大主应力、σ2为中间主应力、σ3为小主应力。
对于轴对称情况下的刚塑性模型的中间主应变为:
ε2=σ2-μ(σ1+σ3)
(4)
式中,μ为岩体的泊松比。
对于轴对称的模型可得ε2=0,带入式(4)可得:
σ2=μ(σ1+σ3)
(5)
联立式(3)与式(5)可得:
(6)
令:
(7)
(8)
(9)
(10)
联立式(6)~(10)可得:

(11)
1.2 极限应力圆包络线
根据双剪强度理论可以得到材料的极限应力圆和包络线如图1所示。根据几何条件可以得到包络线的方程为:
(12)

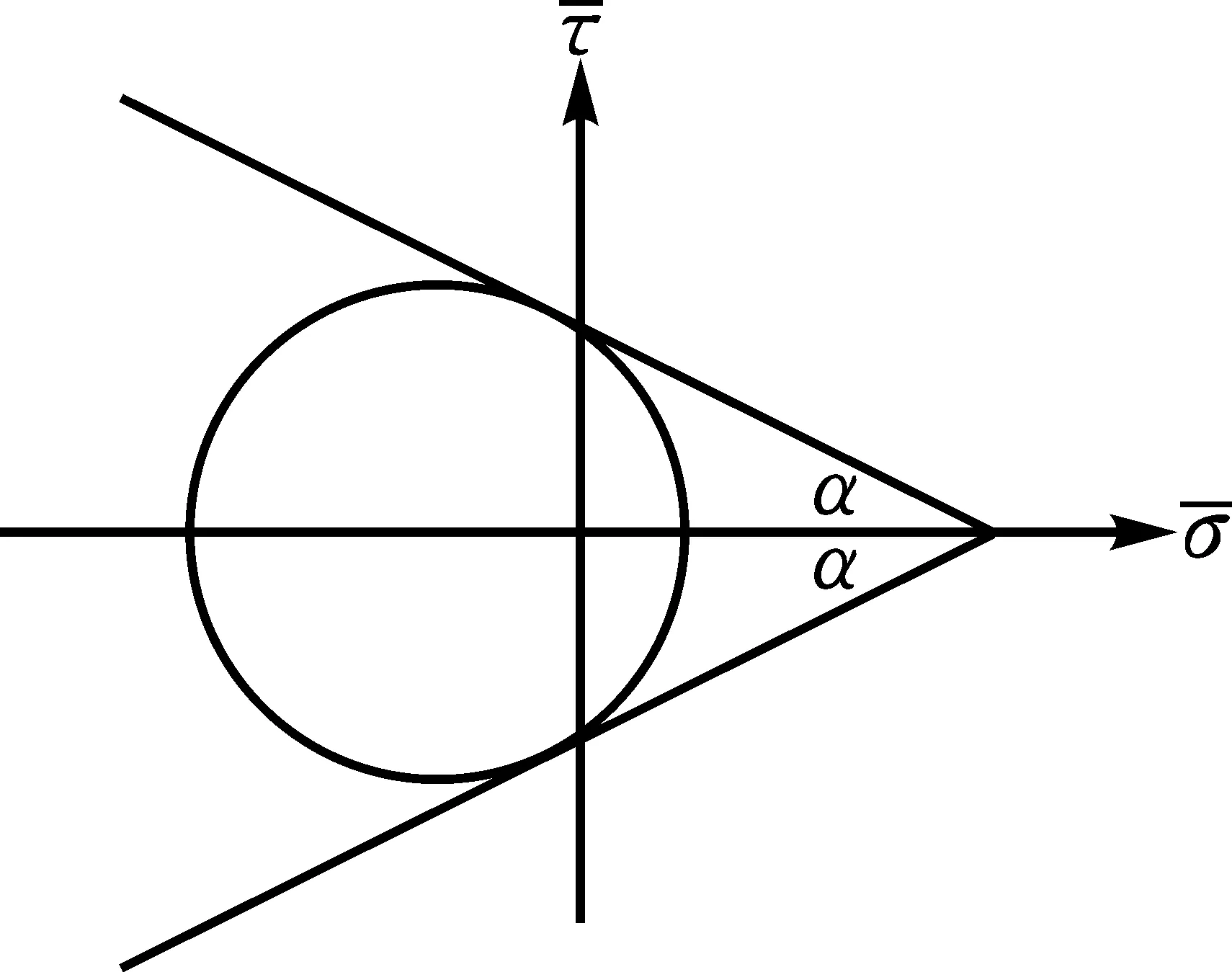
图1 极限应力圆示意图
有几何条件可以得到极限应力的表达式为:
(13)
由式(13)可得:
(14)
由式(14)可得:
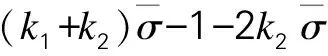
(15)
根据图1和式(12)可得:
(16)
联立式(9)与式(10)得:
(17)
(18)
联立式(17)-(18)得:
(19)
2 岩溶隧道掌子面防突厚度求解
2.1 计算模型的假定
在富水溶腔作用下隧道掌子面的受力机理十分复杂。为了便于理论分析以及保守起见。如图2所示,本文对计算模型做出如下假设:

图2 防突岩墙冲切破坏模式示意图
(1)假定富水溶腔处于隧道掌子面的正前方,且隧道的掌子面为厚度为H的圆板,将该模型视为轴对称问题;
(2)富水溶腔对掌子面的作用力的作用点处于掌子面的中心;
(3)在富水溶腔作用下掌子面自身的重力不计;
(4)掌子面在极限状态下,所形成的冲切体的母线均为直线。
2.2 极限荷载求解
对于掌子面冲切体,在富水溶腔外力的作用下,外力的功率为:
(20)
塑性区的内能耗散率N为:
(21)
式中:A为掌子面冲切体冲切面的面积;σ、τ为冲切面上的正应力和剪应力;εn、γn分别为冲切面上的法向应变率和切向应变率。
根据图2可得:
(22)
(23)
联立式(22)和(23)可得:
(24)
根据塑性区的应服从关联流动法则可得:
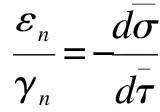
(25)
联立式(24)与(25)可得:
θ=α
(26)
根据式(15)可得:
(27)
联立式(27)与(12)可得:
(28)
由上限法的原理可知,外力的功率与内能耗散功率应相等可得:
(29)
由式(7)、(8)及(29)可得:
(30)
联立式(16)、(22)、(23)、(26)-(28)、(30)可得:

(31)
对式(31)进行积分可得:
(32)
2.3 掌子面防突厚度求解
当富水溶腔与掌子面接触面的相互作用处于极限状态时,应当满足:
q=σc
(33)
联立式(32)、(33)可得:
(34)
由式(34)可以求得掌子面防突厚度为:
(35)
3 工程实例验证
3.1 工程概况
本文的工程实例选自文献[5]中的工程案例进行分析验证。该隧道为处于湖北省的马鹿箐隧道,隧道的布置图如图3所示。该隧道的Ⅰ号线隧道,全长7 879 m,该隧道的Ⅱ号线隧道全长7 832 m,隧道的埋深最大处达到660 m。根据地质勘查报告,在该隧道所处的地层并未发现有断裂构造的存在,隧道穿越的地层主要包含有碎屑岩和碳酸盐的岩地层。该隧道在2006-01-21上午6点隧道平行导洞的施工进行到桩号K255+978段,10点50分时在该桩号的掌子面的拱顶处出现崩溃并发生了严重的突水,直到下午13点10分此次涌水才基本停止。经现场数据分析,此次涌水量最大时达到了30×104m3/h,在平行导洞内测得涌水量达到了300 m3/h。此次突发的岩溶隧道掌子面突水事故造成了多人伤亡。事后施工方合理布置泄水洞对施工所涉及的富水溶腔进行了泄水处理。
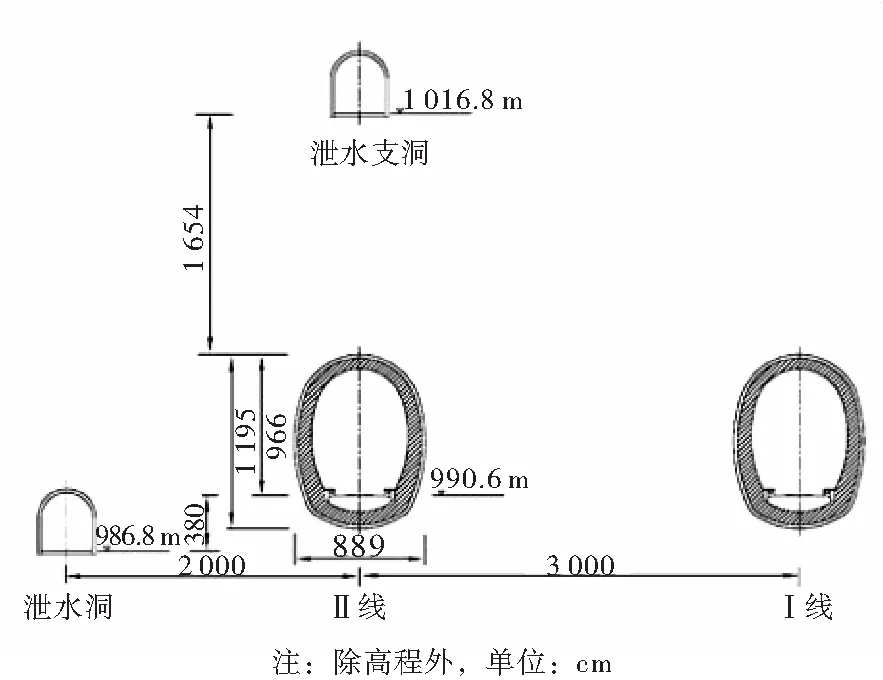
图3 马鹿箐隧道泄水支洞、泄水洞布置平面图
3.2 对隧道掌子面防突厚度进行验证
由《马鹿箐隧道工程报告》可知,该段隧道岩体的岩体力学性质较好,无软弱夹层的出现,岩石的等级可划分为Ⅲ级。根据测量资料显示,该处富水溶腔内的压力为0.8~1.2 MPa。根据该处隧道的工程地质资料,并结合《铁路隧道设计规范》(TB10003-2005),选取岩石的泊松比μ为0.275、岩石抗拉强度σt为1.05 MPa。根据所取得参数可以求得隧道掌子面的防突厚度H为1.295~1.943 m。当富水溶腔内的压力取1.0 MPa,求得的防突厚度H=1.619 m,该结果与文献[6]中预留的掌子面的防突厚度为1.5 m的经验值较为接近,且稍微偏大于经验值,这是因为本文采用了双剪强度理论,考虑了中间主应力对掌子面防突厚度的影响,使得理论计算结果偏于安全。经过已有工程实例的验证,说明本文的计算结果是合理的。
4 结语
(1)本文基于双剪强度准则,考虑了隧道掌子面在受富水溶腔压力作用下,中间主应力对掌子面防突厚度的影响。在此基础上又引入了极限分析上限法原理,并考虑到掌子面的塑性破坏,从而求出了掌子面的防突厚度。
(2)将本文的理论分析结果应用到已有的工程实例当中,并与隧道掌子面防突厚度取值结果吻合较好,且更偏于安全,说明本文的计算分析方法是合理的,可为同类工程提供相应的参考。

