基于积分求导还原思想的新型边坡变形预测UGM(1，1)建模方法

冯学茂

(广西新恒通高速公路有限责任公司，广西 南宁 530021)

0 引言

边坡的变形变化受地质因素和工程因素综合影响，是一个复杂的非线形开放系统[1]。传统的GM(1，1)模型是基于等时距的数据序列进行预测的，而在实际边坡变形监测中，所获得的数据往往并非是等时距的。灰色系统理论的主要思想是以时间距离作为乘数，并将原始数据序列进行一次累加，生成新的序列，从而削弱原始时间序列的随机性[2-3]。UGM(1，1)模型的出现，有效地解决了非等时距数据序列等时距转换问题。传统UGM(1，1)灰色模型先利用实测数据与时区长度的乘积，再通过一阶累加构造新的数据序列，但传统方法构造的数据序列都会与实际情况存在出入。为了缩小两者之间的差距，罗党等人对灰色GM(1，1)模型进行优化，认为灰色模型预测误差主要来自计算式中构造的背景值，并提出全新的背景值构造式[4]；赵晓燕等人提出了对灰色模型平滑改进以提高预测的方法[5]；胡华等人研究了边坡变形监测数据S型函数光滑处理对马尔可夫模型预测结果的影响[6]；姜峰等人将优化的背景值和新信息优先原理运用到传统非等时距灰色模型中，研究表明该方法可以扩大数据有效预测范围[7]；李秀珍等人研究了灰色残差修正模型的滑坡位移灰色预测结果具有很好的修正作用[8]。

在仔细研究了传统UGM(1，1)灰色预测模型的建模原理后，为了提高预测模型的新建序列和实测数据的吻合度，本文从时间序列数据入手，提出一种新的UGM(1，1)模型。该模型基于积分法和近似逼近的思想，利用相邻均值方法，通过一阶累加构造出新的数据序列，使得模拟数据变化情况更加接近实测数据的走势，再通过积分求导还原得到边坡历史累计变形的拟合函数，最后通过实例仿真来验证UGM(1，1)模型在数据模拟和数值预测方面的可行性和可靠性。

1 新型UGM(1，1)灰色预测模型建模原理

1.1 传统UGM(1，1)模型

设有一组不等时距监测数据序列：

X(0)={x(0)(t0)，x(0)(t1)，x(0)(t2)，x(0)(t3)，…，

x(0)(tn)}

(1)

各时段的时间间隔为：

Δti=ti-ti-1；Δtj=tj-tj-1

(2)

式中，Δti≠Δtj；i≠j；i，j∈{1，2，…，n}表示各段时间间隔不等。

传统方法为将不等时距数据序列一阶累加生成新的序列[9]：

(3)

通过数据预测找到数据序列的变化规律，然后根据数据序列的规律变化预测未来可能出现的数值，如果原始序列的变化情况在一阶累加构建新序列过程中没有准确反映，预测模型的模拟与预测精度都会受到影响。传统UGM(1，1)模型的建模原理如图1所示。

图1 不等距序列构造示意图

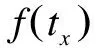
(4)

由此建立的原始序列{x(0)(tk)}与新建序列{x(01)(tk)}之间的关系，表明了数据序列重构是以原始数据变化为基础，保证了新序列的合理性和科学性。

图2 不等距序列误差来源示意图

1.2 新型UGM(1，1)模型

1.2.1 新型UGM(1，1)模型建模原理

对传统UGM(1，1)灰色预测模型的建模原理进行仔细研究之后，针对传统模型的误差来源，通过对一阶累加序列的构建过程和模型的计算方法的改进，提出了一种全新的UGM(1，1)灰色预测模型。该新模型的建模原理如下：

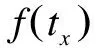
(5)

(2)在预测监测点的边坡变形时，基于连续函数积分求导还原思想，通过对预测模型所求得的面积变化的时间响应式求导还原得到监测点的累计变形时间序列方程。

如图3所示，通过区间相邻均值与区间长度的乘积的变化值近似表示时间响应方程在区间上的增量，灰色模型模拟和预测的准确性就可以利用面积近似逼近来实现提高。

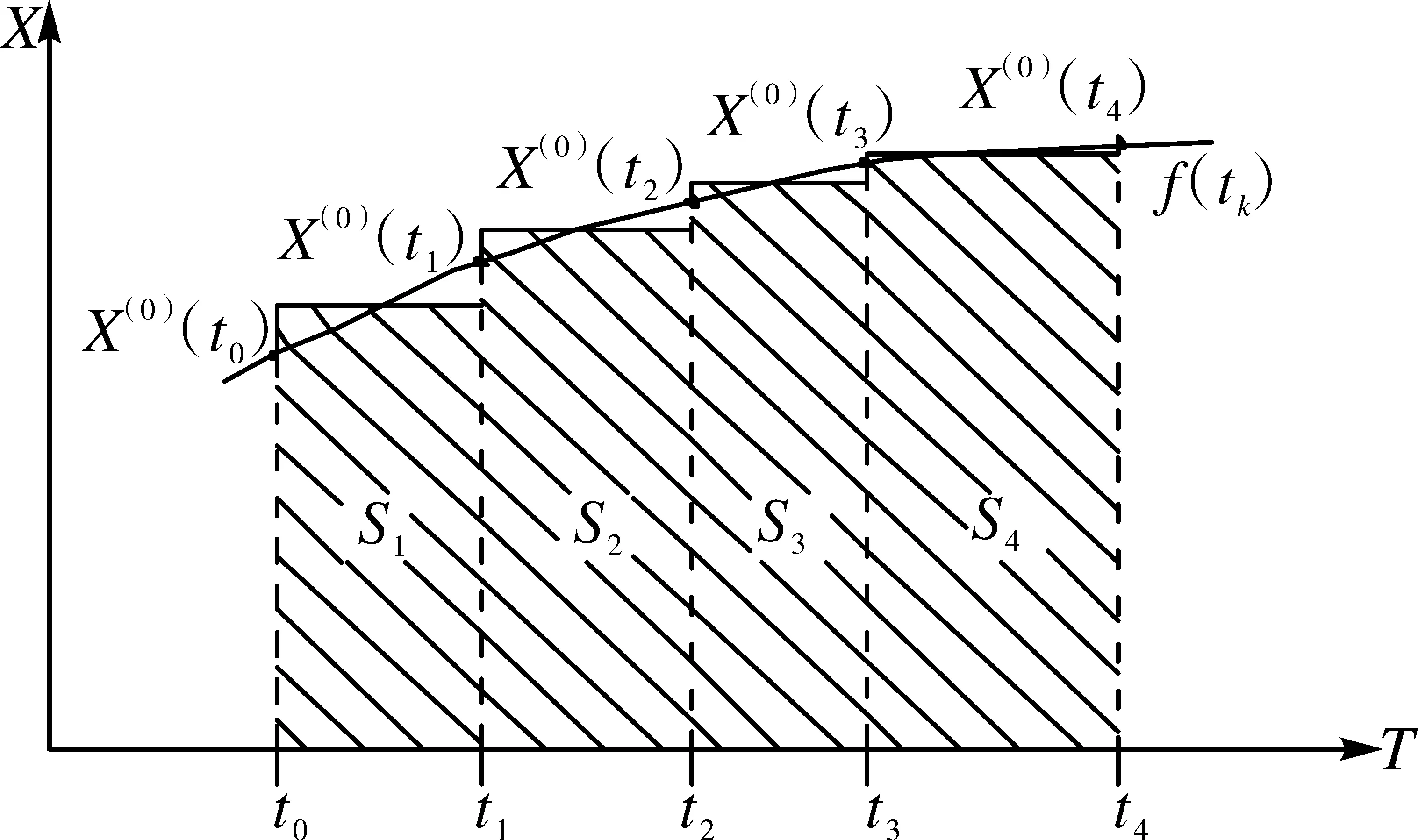
图3 相邻均值法示意图

1.2.2 新型UGM(1，1)模型构建

设有一组不等时距监测数据序列：

X(0)={x(0)(t0)，x(0)(t1)，x(0)(t2)，x(0)(t3)，…，x(0)(tn)}

(6)

各时段的时间间隔为：

Δti=ti-ti-1；Δtj=tj-tj-1

(7)

式中，Δti≠Δtj；i≠j；i，j∈{1，2，…，n}表示各段时间间隔不等。

建模前，将原始序列中任意两个相邻实测数据取均值得到一组新序列：

(8)

处理后的数据序列即为：

X(00)={x(00)(t1)，x(00)(t2)，x(00)(t3)，…，x(00)(tn)}

(9)

对处理后的不等时距数据序列进行一次累加：

X(01)(tk)=x(00)(t1)×Δt1+x(00)(t2)×Δt2+…+x(00)(tk)×Δtk

(10)

(11)

后续步骤与传统UGM(1，1)模型建模基本保持一致，采用最小二乘法解得新UGM(1，1)模型中时间响应方程[10-11]：

(12)

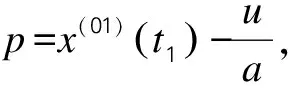
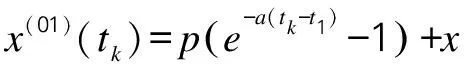
(13)

(14)

(15)

2 新型灰色预测模型在边坡位移中的算例分析

以某高速公路路基边坡位移监测为例，选取其中一组监测数据作为依据，使用新型UGM(1，1)预测模型对原始监测数据序列建模并预测位移，以此来验证新模型在数据模拟与预测方面的准确性与有效性。边坡位移实测数据如表1所示。

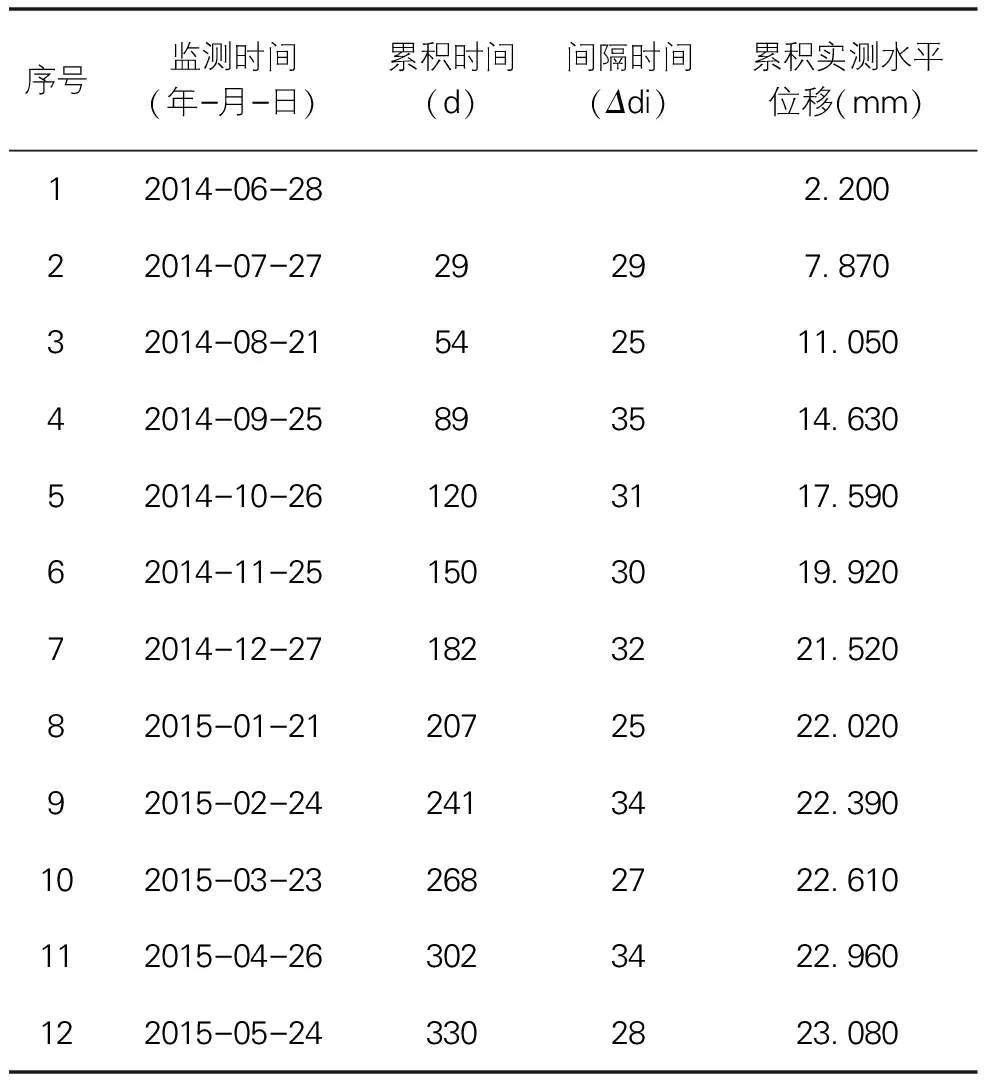
表1 监测点监测数据表

2.1 模型建模及计算过程

根据灰色模型GM(1，1)适用范围的讨论结果[12-13]，发现当初始数据恒正且为凹函数时是其最佳的适用范围；又因灰色预测模型的时间序列方程是基于指数函数建立的，本文将对计算的每一阶段的数据进行处理，使其时间-位移曲线为呈恒正的凹函数形式。

(1)初始序列

由表1，将实测数据处理后构成的原始数据序列为：

x(0)={x(0)(t1)，x(0)(t2)，…，x(0)(t10)}

={22.80，17.13，13.95，10.37，7.41，5.08，3.48，2.98，2.61，2.39，2.04}

(16)

(2)新建序列

原始位移数据一阶累加生成的新序列为：

x(01)={x(01)(t1)，x(01)(t2)，…，x(01)(t10)

={578.985，967.485，1 393.085，1 668.675，1 856.025，1 992.985，2 073.735，2 168.765，2 236.265，2 311.575}

(17)

(3)时间响应式

与传统方法一样通过最小二乘法来计算出灰色参数，并得到新型UGM(1，1)预测模型新建序列的时间响应式：

(18)

根据初步得到的模型模拟结果与实测数据的差值，同样采用相邻均值方法建立对应的残差模型如下[14]：

一次残差修正：

(19)

二次残差修正：

(20)

最终得到传统灰色UGM(1，1)预测模型的时间序列方程为：

(21)

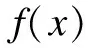
2.2 预测结果分析

通过建模计算取得的灰色预测模型的时间响应式，对路基边坡变形位移的预测结果分析如表2和图4所示：

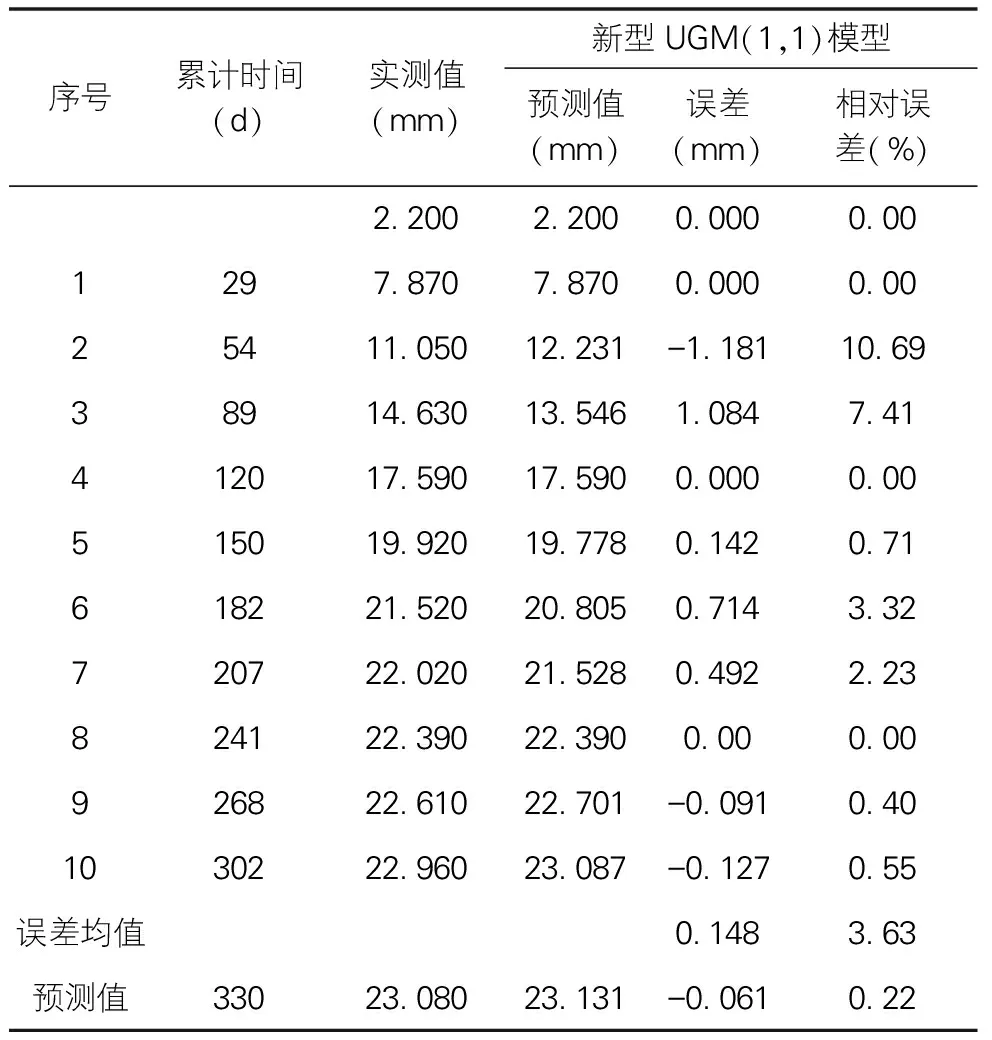
表2 新型UGM(1，1)灰色预测模型预测结果分析表

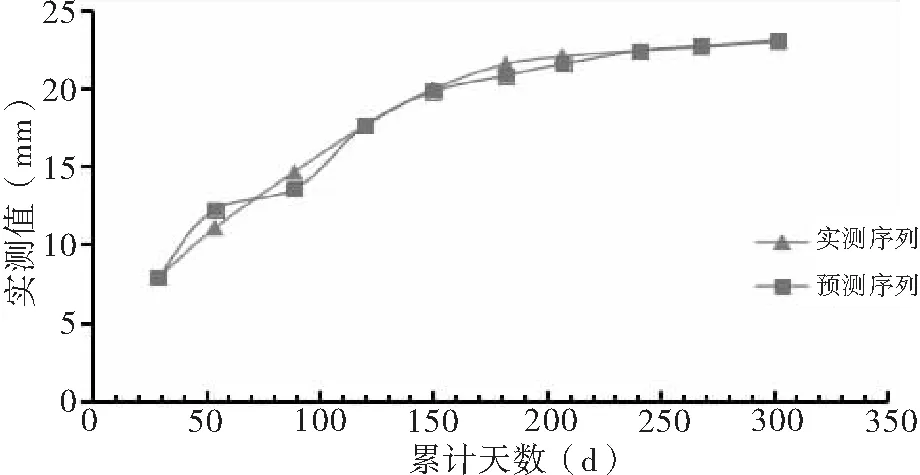
图4 边坡位移预测模型拟合预测图

3 结语

本文所述的新型UGM(1，1)灰色预测模型是通过研究传统预测模型的误差来源和传统UGM(1，1)灰色预测模型建模原理提出来的。以某高速公路一段路基边坡实测数据为依据来验证新型UGM(1，1)灰色预测模型的模拟和预测效果，初步得到以下结论：

(1)新型UGM(1，1)灰色预测模型的模拟曲线与实测曲线非常吻合，且其预测数值的误差为0.22%，远小于5%的合理范围，说明新型UGM(1，1)灰色预测模型可以用作数值灰色预测。

(2)经过两次残差修正，新UGM(1，1)灰色预测模型生成的时间响应方程随着实测数据缓慢趋于稳定，其模拟的误差逐步缩小，说明了新模型适用于对变化平缓且逐渐趋于稳定的数据序列进行模拟与预测。

(3)对于逐渐趋于稳定的数据序列，模型残差修正是一个循序渐进的过程。前期残差修正是调整预测模型的时间响应式的整体走势；后期残差修正则是进行局部微调。

(4)新型UGM(1，1)模型数据预测的精度会随着时间的延续而下降，初步分析预测与灰色预测模型的时效性有关。建议今后研究中引进等维新息方法对数据进行新陈代换[15-16]，通过数据序列的不断更新来提高灰色模型的预测精度。

结论分析表明，在数据预测方面，新型UGM(1，1)灰色预测模型具有一定的可行性和可靠性，对发展和优化非等时距灰色预测模型具有一定的参考意义。