面向公有云的数据完整性公开审计方案

缪俊敏,冯朝胜,2,李 敏,刘 霞

(1.四川师范大学 计算机科学学院,成都 610101; 2.电子科技大学 信息与软件工程学院,成都 610054)(*通信作者电子邮箱csfenggy@126.com)

0 引言

云存储已引起学术界以及其他各行各业的广泛关注,但这种新的数据存储模式也带来了许多安全挑战[1],其中之一就是如何确保在半可信服务器上的用户数据完整性。数据审计是确保云数据完整性的重要方法,现有方案分为公开审计和私有审计两大类。私有审计因为由数据所有者负责,故不存在隐私泄漏给第三方审计者(Third Party Audit, TPA)的问题,不足是审计时要求数据所有者在线且需要消耗其主机资源;而公开审计无需数据所有者在线且不会占用其资源,但需考虑数据泄漏给第三方的问题。另外,由于用户及TPA都未保存原数据,所以需要一个有效的方法判断审计过程中云存储服务器(Cloud Storage Server, CSS)是否按照要求计算返回对应数据块的相关数据。

本文基于MHT-PA(Merkle Hash Tree-Public Auditing)方案[2-3]提出了一种面向公有云的数据完整性公开审计方案,该方案在支持动态更新和批量审计的基础下实现了针对第三方审计者的隐私保护，并避免了针对CSS的替代攻击。

1 相关研究

Deswarte等[4]在2003年提出了第一个基于RSA(Rivest-Shamir-Adleman)的远程数据审计方案,几年后,Ateniese等[5]使用同态可验证标签技术[6]首次提出支持公开审计的可证明数据持有(Provable Data Possession, PDP)方案并在文献[7]中进行改进，提出了可扩展PDP模型，以支持动态操作；但该方案并不支持数据块插入。次年,Erway等[8]首次探索动态PDP方案架构,提出了基于等级的认证跳表(Rank-based Authenticated Skip List, RASL)概念,并在之前的可扩展PDP模型基础上废除了标签索引信息以实现支持包括数据插入的完全数据更新操作的PDP方案；但该方案不支持批量审计和数据隐私保护。由于PDP方案仅支持验证数据的完整性,不能保证数据的可恢复性。Juels等[9]提出了一个专注于大文件静态存储的可恢复证明(Proof of Retrievability, PoR)方案,但挑战次数有限。Shacham等利用BLS(Boneh、 Lynn和Shacham)签名[10]在文献[11]中提出了一个支持公开审计的紧凑PoR方案,但该方案同样只支持静态数据且容易泄露用户隐私信息。

Wang等利用同态可验证标签技术和数据分段技术先后在文献[2,12-13]中引入TPA提出了云数据完整性公开审计方案,以克服以上方案的不足，他们在文献[12]中提出了在分布式情况下考虑动态数据存储且能定位错误数据的云存储安全性方案；后在文献[2]中引进Merkle哈希树(Merkle Hash Tree, MHT)提出了新的改进方案,其可应用在PDP或PoR方案中,支持完全数据更新操作,且TPA能高效进行数据完整性批量审计，但该方案引入了新的隐私泄漏问题。虽然文献[13-14]利用同态密钥随机掩码技术解决了此问题,但本文中的哈希值混淆法在解决问题的基础上减少了对应审计阶段的TPA计算量。文献[15]在文献[2]基础上通过改进MHT实现了支持细粒度更新数据的功能,文献[16]则将多个副本的MHT合并成一个MHT以提高效率；但这些方案都会带来CSS在数据不完整的情况下仍可伪造应答证据欺骗审计的安全问题,本文利用基于MHT的覆盖树加强了审计过程，避免了半可信的CSS发起此伪造攻击。

2 MHT-PA方案

2.1 方案概要

MHT-PA方案[2]如图1所示。客户端首先将文件预处理后化分成多个数据分块,对每一个数据分块进行签名得到签名集合,再创建一棵Merkle哈希树,并对根节点签名。最后将原文件、签名集合、根节点签名值及一些附加信息一并存入CSS。客户端做了审计委托后当TPA需要审计时,由TPA选取部分数据块,并为每个数据块选取一个随机数,组成一个挑战请求发送给CSS。CSS收到挑战请求之后通过块索引找到相应数据块及其标签,计算出证据返回给TPA。TPA随后验证收到的证据从而判断云数据的完整性。

图1 MHT-PA方案基础架构Fig. 1 Basic architecture of MHT-PA

其方案具体实现过程如下:

构建双线性映射e:G×G→GT,其中G和GT是乘法循环群,生成元为g,大素数阶为p,令一个映射到G的散列函数H(·):{0,1}*→G,一个映射成定长字符串的散列函数h(·)。

1)初始化阶段。客户端首先将文件F预处理后化分成n个数据分块mi(i∈[1,n]),其中mi∈Zp。选择一个随机数α∈Zp,并计算出υ←gα,再另外随机选择一对签名公私钥(spk,ssk),形成最终的公私钥对,其中私钥为sk=(α,ssk),公钥为pk=(υ,spk)。在G中随机选择一个元素u,结合文件名name,文件块数n及对其的签名得到文件标签t=(name‖n‖u‖ssigssk(name‖n‖u)),对文件的每个数据块进行签名σi=(H(mi)·umi)α,得到文件签名集φ={σi|1≤i≤n}。同时创建以{h(H(mi))|1≤i≤n}为叶子节点的MHT,用私钥α对根节点R进行签名得到sigR=(H(R))α。最后,客户端将{F,t,φ,sigR}发送给CSS,并将本地存储删除。

2.2 方案的不足

MHT-PA方案支持第三方公开审计协议以及完全动态数据更新操作,用户利用私钥对数据块进行签名后,TPA利用公钥即可完成审计工作。相对于Juels等[9]提出的方案,该方案的验证次数不受限制。方案中使用的签名标签具有同态特性,使得云服务器生成证据时,能够将多个值聚合成一个值,从而减少通信开销。但是MHT-PA方案存在两个问题：一方面由于MHT-PA方案没考虑数据的隐私保护,用户的隐私信息可能会泄漏给TPA；另一方面,为了支持完全动态数据操作,去除了文献[9]和文献[11]方案中签名的索引信息,用H(mi)替换h(v‖i)和H(name‖i),使得TPA不能通过自身保存的索引号{s1,s2,…,sc}验证返回的证据正确性,因而云存储服务端由于各种原因可以不按要求,而根据已有数据伪造应答证据,而伪证据不能被MHT-PA方案的审计策略所识别,依然能通过验证。

2.2.1 泄漏用户隐私

半可信的TPA对相同的数据块发起多次审计请求后会收到CSS返回的多条审计证据,通过分析并处理这些证据信息可以恢复出用户的数据信息,具体过程分析如下。

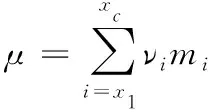
(1)

由于方程(1)的系数行列式不重复且不为零,TPA可以通过拉格朗日插值法或高斯消元法计算得到{mx1,mx2,…,mxc}的值,从而获取用户信息,致使用户数据信息不安全。

2.2.2 CSS证据替代

MHT-PA方案中,TPA自身保存的索引号失去了验证CSS返回数据正确性的作用后,数据块信息mi在脱离原始文件后也不再为用户所知,而用户和TPA都未保存,且TPA也不能获取mi,无法计算出H(mi),因此必须交由CSS计算,且没有一种有效的方式验证其是否按正确的顺序返回正确的H(mi)。在源文件增、删、改后,所创建MHT的树结构不一定为简单的满二叉树且用户和第三方都未保存,只能由CSS返回。然而,半可信的云服务提供商可以利用这些优势操控MHT以及H(mi)和mi,用其他数据块作替代,伪造证据欺骗验证者。

假设CSS保存的文件MHT如图2所示。TPA想要通过验证数据块m1和m2来检查文件的完整性。若文件完整且云存储服务端正常返回,则顺利通过验证并返回TRUE,但当云存储服务端中m1和m2数据不完整或其他某种原因时,便可用已有的正确数据如m3和m4来计算得到证据返回给验证者TPA。

图2 文件的MHT示例Fig.2 Example of MHT authentication of data elements

首先,若CSS正常返回,TPA通过返回的H(m3)和H(m4)以及伴随节点信息h(b)和h(d)构造出图3(a)的树得出正确的R通过第一步验证,但由于各种原因,CSS把已有的数据H(m3)和H(m4)以及伴随节点信息h(b)和h(e)发送给TPA,TPA收到这些数据过后,无法判断数据正确与否,按照CSS的想法构造出图3(b)的树且同样能得出正确的根节点R的值,进而顺利通过第一步验证:e(sigR,g)=e(H(R),gα)。

图3 替代攻击示例Fig. 3 Example of alternative attack

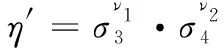
(2)

式(2)左边:

e((H(m3)·um3)ν1·(H(m4)·um4)ν2,gα)=

e((H(m3)ν1·uν1m3)·(H(m4)ν2·uν2m4),υ)

式(2)右边:

e(H(m3)ν1·H(m4)ν2·uμ′,υ)=

e(H(m3)ν1·H(m4)ν2·uν1m3+ν2m4,υ)=

e((H(m3)ν1·uν1m3)·(H(m4)ν2·uν2m4),υ)

可见,式(2)成立,第二步验证也同样通过。因此,云存储服务端通过伪造的证据成功欺骗了TPA。

3 本文公开审计方案

3.1 改进策略

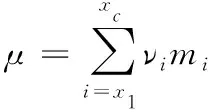
图4 TPA和CSS所得覆盖树示例Fig. 4 Examples of overlay trees calculated by TPA and CSS

采取如下步骤和措施防止CSS操控MHT和H(mi)进行审计替代:1)TPA在发起正式验证挑战前先向CSS请求压缩后的文件MHT树结构。解压后简单判断树的叶子节点数与文件数据块数目是否相等,若不等则直接返回FALSE。2)根据文件的MHT树结构选取要验证的数据块,由这些数据块序号和MHT树结构得到覆盖树(即能从所选叶子节点出发由下往上涉及最少节点数得到根节点的树，其为MHT的子结构)的树结构T(如图4(a)所示)并保存待用。3)CSS接收到TPA挑战请求后亦由这些数据块序号和MHT得到覆盖树T′(如图4(b)所示)作为证据的一部分返回。4)TPA在接收到证据后首先匹配两棵覆盖树的结构，匹配成功后方才将{H(mi)|x1≤i≤xc}依次取出存储,并计算出对应的{h(H(mi))|x1≤i≤xc},进而求得R进行下面的验证。

3.2 方案描述

3.2.1 初始化阶段

令双线性映射函数e:G×G→GT,其中G和GT是乘法循环群,且生成元为g,大素数阶为p。令H(·)是映射到G域的散列函数{0,1}*→G,f(·)是映射到Zp域的单向散列函数:{0,1}*→Zp,h(·)是基于安全哈希算法(Secure Hash Algorithm, SHA)的散列函数[17]。

1) 生成公私钥对KeyGen(1k)→(sk,pk)。

由客户端执行,生成方案基本参数。根据输入的安全参数1k选择一个随机数α∈Zp作为主私钥,计算出公钥υ=gα,再随机产生一个附加签名公私钥对(spk,ssk),形成最终的私钥sk=(α,ssk)以及公钥pk=(υ,spk)。

2)生成同态签名集SigGen(sk,F)→(φ,sigR)。

由客户端执行,生成数据块的签名及验证元数据,并将其传入CSS中存储。首先将文件F用里德所罗门编码(Reed-Solomon Codes)[18]预处理,划分成n块数据块mi(i∈[1,n])∈Zp。在G中随机选择一个元素u,结合文件标识FName和文件数据块总块数n,再用附加私钥ssk对这三元组做签名得到文件标签t=FName‖n‖u‖sigssk(FName‖n‖u)。利用私钥α和元素u对每个数据块mi进行签名得到σi=(H(mi)·u(mi f(mi)) mod p)α∈G,构成同态签名集合φ={σi|1≤i≤n}。构建以数据块哈希值{h(H(mi))|1≤i≤n}为叶子节点的MHT,对树的根节点签名得到sigR=(H(R))α,最后把元组{F,t,φ,sigR}发送CSS并将本地文件存储删除。

3)云存储初始化CSSInit(F,t,φ,sigR)。

由CSS执行,做相关初始化操作。接收到用户的源文件和签名信息等数据后,先做相应存储,当第一次接收到用户增删改请求或TPA的审计请求时构建以数据块哈希值{h(H(mi))|1≤i≤n}为叶子节点的MHT,并将其结构或部署策略保存。

4)审计委托AudDel(FName)。

由客户端执行,把需第三方审计的文件标识告知给TPA,作审计委托。

3.2.2 审计阶段

1)验证准备PreChal(pk,t,tree)→(I,T)。

由TPA执行,为发起正式审计挑战做基础检查及相关准备。TPA先向云存储服务端获取文件标签t以及压缩后的MHT树结构tree,并用附加公钥验证标签,若验证通过则取出文件块数n及验证时需用的元素u。根据得到的文件结构树tree,判断其根节点数,即文件块数是否等于n,若不等则直接返回FALSE中止审计,反之分析树结构,从数据块索引[1,n]中选取需要验证的c个最优元素,构成有序的索引子集I={s1,s2,…,sc},其中s1≤s2≤…≤sc。根据tree及序号集I计算出覆盖树T(节点不含值)并保存。

2)发起挑战StatGen(1k)→(chal)。

⑲OECD，Competitive Neutrality:Maintaining a level playing field between public and private business，Paris:OECD Publishing，2012，p．53．

由验证者TPA执行,向CSS发起正式的审计挑战。对集合I中每一个值i,选择一个随机数νi∈Zp,形成一个挑战请求chal={(i,νi)|i∈I}发送给CSS。

3)生成证据ProofGen(F,φ,chal)→proof。

4)验证证据ProofVerify(pk,proof,T,chal)。

由TPA接收到CSS传回来的证据后执行,验证证据返回TRUE或FALSE。第一步,判断CSS端返回的覆盖树T′和自身计算的覆盖树T的树结构是否相同,若有异则直接返回FALSE;反之,从覆盖树T′中提取{H(mi)|s1≤i≤sc}另存后,计算出{h(H(mi))|s1≤i≤sc}替换对应值,若各叶子节点完整则可计算出根节点R。第二步,验证式(3)判断根节点R的值是否正确,若验证失败,说明返回的{H(mi)|s1≤i≤sc}数据有误或者其他挑战验证外的数据块信息错误,直接返回FALSE。第三步,检验式(4)是否成立,其中{H(mi)|s1≤i≤sc}已在第一步中得到。

e(sigR,g)=e(H(R),gα)

(3)

(4)

3.2.3 动态更新

本文方案支持完全动态更新操作,由于更新操作不涉及第三方,所以不存在对TPA的隐私保护问题。方案增加修改删除数据块操作与MHT-PA方案相同,具体操作请参看文献[2]。

4 安全性及性能分析

4.1 安全性分析

本文方案的安全性基于CDH问题(Computational Diffie-Hellman problem)难以求解,且经过里德所罗门编码后的文件可以在可忽略不计的差错下恢复出原始文件,以上两点在文献 [2] 中已经证明,由于篇幅所限,本文不再赘述具体证明过程。本文方案的正确性及安全性,主要提供两方面的证明:1)TPA在审计云数据过程中无法获取或分析得到用户数据信息；2)CSS无法用其他手段伪造证据欺骗TPA。

定理1 基于所提出的公开审计方案,TPA在审计云数据过程中无法获取或分析得到用户数据信息。

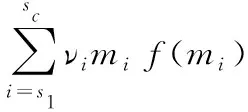
(5)

由于TPA未从云服务端获取f(mi),也不能从已知信息中提取出f(msc),所以不能通过方程组(5)恢复出具体的{ms1,ms2,…,msc},从而保护了用户隐私。

定理2 所提出的公开审计方案能防止CSS进行替代攻击。

证明 CSS不能通过已保存的数据块替代所要求的数据块,伪造出能通过第三方审计的应答证据。假设文件经过客户端数据增删改更新操作请求并执行后的MHT结构如图5所示,CSS无法重建一棵拥有相同节点数、相同根节点值且满足任意数据块组合挑战的MHT,只得把正确的MHT树结构发送给TPA。

图5 更新过的文件MHT示例Fig. 5 Example of modified MHT

表1 云数据完整性审计方案的对比Tab. 1 Comparison of different remote data integrity checking schemes

TPA得到MHT树结构后,想要通过验证m3、m4和m6数据块判断文件完整性,并得出如图6的覆盖树树结构T。当收到TPA审计挑战请求后,CSS必须返回同T结构的覆盖树T′。基于SHA不会将不同字符串哈希成相同结果的假设,CSS必须得拥有正确的H(m3)、H(m4)和H(m6)且按正确的顺序返回才能让TPA计算出对应正确的节点h(H(m3))、h(H(m4))和h(H(m6)),且h(c)和h(d)合并计算出的哈希值与h(d)和h(c)合并计算出的哈希值不一样,避免对称值替代攻击。结合T′中伴随节点h(c)、h(H(m5))和h(e)的正确值,才能从下至上计算出正确的根节点值,使得e(sigR,g)=e(H(R),gα)通过第二步验证。证明过程如下:

e(sigR,g)=e(H(R)α,g)=e(H(R),gα)

(6)

图6 安全性分析中覆盖树示例Fig. 6 Example of overlay tree in security analysis

基于SHA不会将不同字符串哈希成相同结果的假设,且h(c)和h(d)合并计算出的哈希值与h(d)和h(c)合并计算出的哈希值不一样,不支持交换,所以保障了H(mi)顺序正确,也防止了对称值替代。

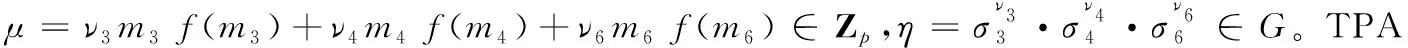
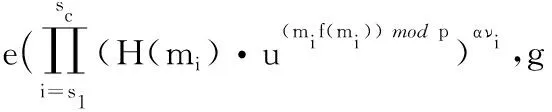
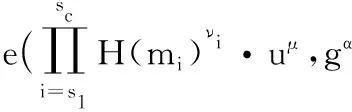
4.2 性能分析

通过分析本文方案与现有几种具备代表性的云数据完整性审计方案,对比了其特征及性能,其中检测率表示对于出错率为θ的文件,抽样审计c个数据块,至少一个数据块被检测到的概率为1-(1-θ)c。结果如表1所示。

从表1中可知,本文方案在支持公开审计和完全动态数据更新操作的基础上,更具隐私保护和防止CSS替代攻击特征,在计算开销、通信开销和存储开销的性能上,与大多方案具有相同复杂度数量级,即相似的性能。

5 实验结果分析

本文方案在理论分析的基础上进行了仿真测试实验。操作系统为macOS 10.13.1,处理器为2.7 GHz Intel Core i5,8 GB 1 867 MHz DDR3存储器的环境下利用python语言实现,相关密码运算基于pythia-pyrelic三方库[19],采用Barreto Naehrig 曲线[20]和SHA256哈希算法,以80比特安全参数及256比特曲线大素数阶为基础参数,所有测试结果均为18次实验的平均值。

本文选择了MHT-PA方案和文献[15]方案与本文方案做对比实验,比较了其在相同文件下以1 024字节划分数据块,挑战验证不同数据块数目的计算开销与通信开销。不同挑战验证块数下三种方案的CSS计算时间和TPA计算时间如图7所示。从图7可看出，CSS和TPA的计算时间与验证的数据块数目紧密相关,随着所需验证的数据块数目增多,TPA和CSS的计算时间都会相应增加。

图7 挑战验证不同数据块数目下计算开销Fig. 7 Computation costs with different verification data blocks

图8表示同样大小的文件在验证不同数据块数目下的通信开销,由图8可知,本文方案相比另外两种方案增加了一些通信开销,此即为挑战前TPA向CSS所请求的一个树结构。从整体角度看,这个开销可忽略不计。

图8 挑战验证不同数据块数目下的通信开销Fig. 8 Communication costs with different verification data blocks

表2 三种方案挑战验证320和460个数据块下的性能比较Tab. 2 Performance comparison of three schemes for verifying 320 and 460 data blocks

由于文献[21]已经证明在文件数据块出错率为1%的情况下,若要达到99%或95%的验证准确率,则随机抽取460个或320个数据块即可,因此本文详细分析比较了在验证320个和460个数据块下的性能，实验结果如图9所示。从图9中可知,在验证相同数据块数目时,本文方案的CSS计算时间略高于另外两种方案,TPA计算时间几乎相同,但从整体来看,三种方案计算开销的差距可忽略不计。

图9 挑战验证320和460个数据块下的计算开销Fig. 9 Computation costs for verifying 320 and 460 data blocks

表2综合展示了MHT-PA方案、文献[15]方案与本文方案在95%和99%的验证准确率下，即TPA分别挑战验证320个数据块和460个数据块，三项性能指标，即TPA计算时间、CSS计算时间和通信开销的结果对比，表中各项值均为18次实验的平均值。

综上所述，在以TPA挑战验证的数据块数目为唯一变量的前提下，以上三种方案的计算开销和通信开销都会随着此变量的增大而增加。在TPA验证相同数据块数目下，本文方案的计算开销和通信开销相比另外两种方案有些许增加，其中CSS的计算开销增加率相对高一点。而当TPA审计需达到的准确率越高时，本文方案的计算开销增加率和通信开销增加率将会越低。

6 结语

本文在MHT-PA方案基础上提出了一个新的面向公有云的数据完整性公开审计方案,利用哈希值混淆方法更改了文件的同态认证标签，使TPA无法从CSS返回的证据信息中计算得出用户数据信息，从而解决了用户隐私泄露给TPA的问题；其次，提出覆盖树概念，调整了审计策略，让TPA在正式审计前先进行基于MHT的覆盖树结构匹配,解决了半可信的CSS发起替代审计攻击的问题,通过理论和实验分析测试了方案的性能,验证了该方案的正确性和有效性。