ADRC在光通信APT系统下的扰动分析及参数整定

王 森, 史红伟, 李明秋

(长春理工大学电子信息工程学院，长春 130022)

0 引言

传统的控制算法在APT系统下存在一些问题，例如控制系统建模困难、扰动抑制能力受到机械谐振制约等，这些问题影响了控制精度的提高。提升控制精度的根本在于扰动的抑制。对于APT系统内外扰动的解决方法，国内已取得许多成果。文献[1]对传递函数进行参数辨识并将系统带宽进行优化，使系统带宽大幅提高;文献[2]提出误差自适应前馈控制方法，提高了系统抑制光束抖动的能力。韩京清教授提出的自抗扰控制策略[3-4]，将系统受到的所有扰动归结为一个单独扰动，以此达到抑制扰动的目的，使系统有更强的鲁棒性和适应性。

本文将自抗扰控制策略应用于空间光通信APT系统，并分析了自抗扰控制下的参数对APT系统的扰动影响，然后使用线性自抗扰的控制方法，针对扰动做了参数整定，结果证明，自抗扰控制策略对精跟踪部分的扰动抑制性能提升明显，并且对APT系统的控制精度有了进一步提高。

1 APT精跟踪系统自抗扰控制结构及扰动分析

精跟踪系统结构及其工作过程如图1所示。

图1 精跟踪系统结构图Fig.1 Structure of fine tracking system

CMOS接收到信标光的信号，经图像处理和光斑中心位置提取后，由精跟踪控制器计算FSM的偏转角度，计算后通过D/A模块将控制器的数字信号转换为电压信号，从而驱动4个PZT运动，以控制FSM偏转，在FSM的作用下，光斑移动到CMOS中心，完成控制任务。

精跟踪系统结构中，PZT与FSM可以看作二阶震荡环节，压电陶瓷的滞环现象、驱动器的蠕变过程以及CMOS传感器的延迟可以近似成一个一阶惯性环节[5]，传递函数可以表示为

Gd(s)=1/(Ts+1)

>。

(1)

D/A的数学模型可以看成比例环节KD/A,快速反射镜的数学模型为二阶振荡环节[6]。

为了减小光斑检测单元和视频信号处理单元对数字伺服单元的影响,需要使图像部分的帧频达到闭环带宽的10倍以上,由它引起的相位稳定裕量减少不超过5.7°，对精跟踪单元的稳定影响较小，可在仿真中忽略。

则精跟踪的开环模型为

(2)

卫星在空间中运行不可避免地存在自身的机械震动，这个震动是不可消除的。为了模拟真实的环境，根据欧洲航天局(EAS)对OLYMPLUS卫星进行的星体震动测试，对星间光通信影响较大的震动频率主要在100 Hz以内[7]，功率谱密度函数为

S(f)=160/(1+f2)

>。

(3)

其功率谱曲线如图2所示。

由此功率谱曲线设计了一个模拟星体震动的滤波器，形式为

(4)

根据文献[8]可知，线性自抗扰的参数主要有b0,ωc,ωo，在其文章中引入了新的带宽概念，其中，ωc为控制器带宽，ωo为观测器带宽。带宽概念的引入，方便了线性自抗扰控制器的参数整定，大大宽泛了线性自抗扰策略在工程实际中的应用。文献[8]提到的线性状态观测器(LESO)为

(5)

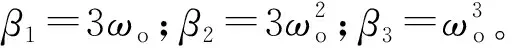
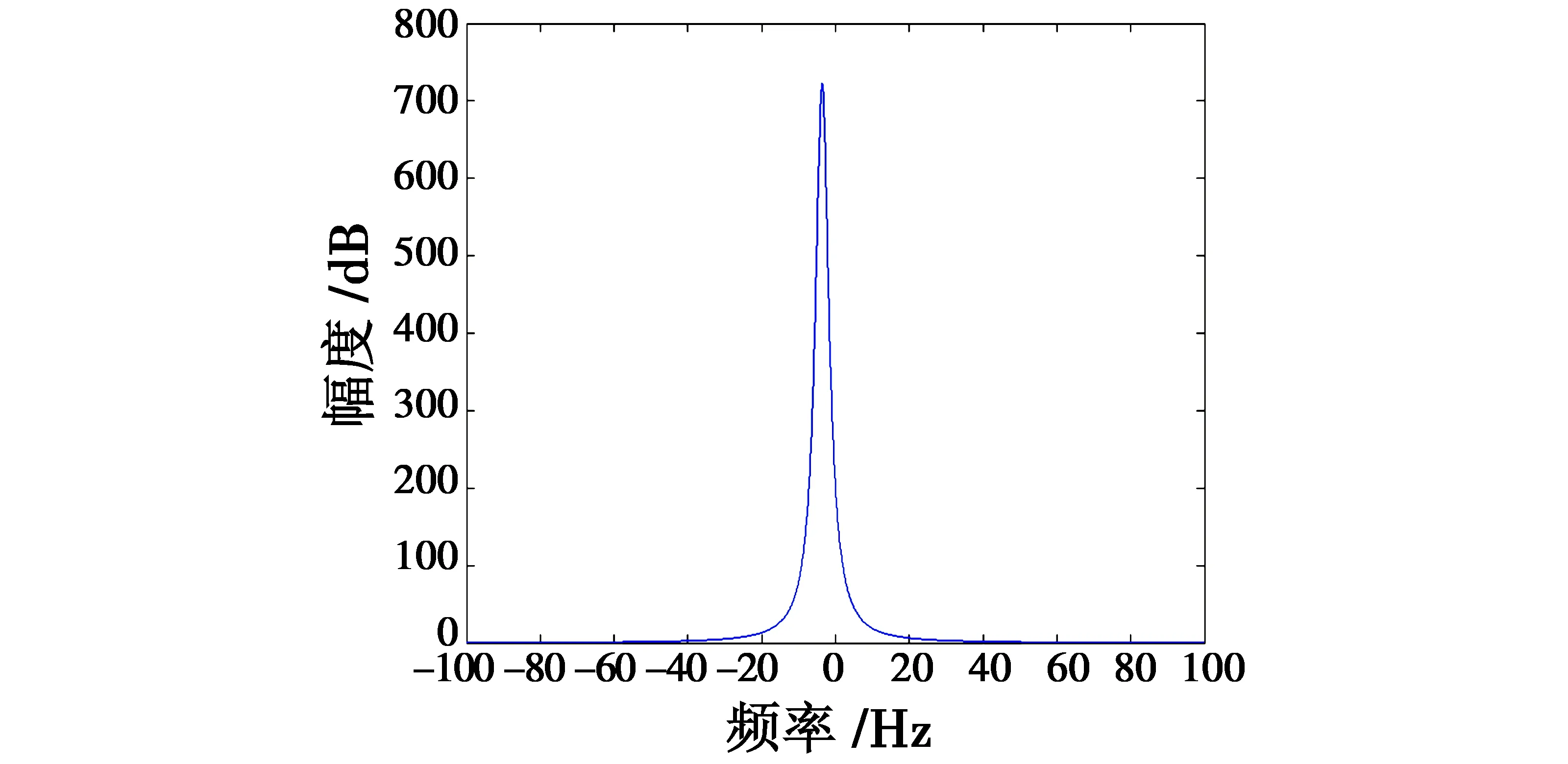
图2 OLYMPLUS功率谱曲线Fig.2 Power spectrum curve of OLYMPLUS

根据式(4)和式(5)推导可得

(6)

在这里重点考虑系统的观测噪声δo和系统控制输入端的噪声δc对LESO的影响，由式(6)可得系统观测噪声δo的传递函数为

(7)

其波特图如图3所示。

图3 噪声扰动Bode图Fig.3 Bode diagram of noise disturbance

由图3可以发现，线性系统观测器中，随着ωo增加,系统响应速度加快,同时系统的高频带增益随之增加,从而使系统对噪声放大作用变得明显。

同理可求得系统控制输入端扰动δc的传递函数为

z1/δc=b0s/(s+ωo)3>。

(8)

选取b0=10，ωo为10，20,30,40,50,可得如图4所示的频域特性。

由图4可以发现，系统的状态观测器带宽ωo的增加可以减小观测器跟踪信号的相位滞后,且基本不影响系统在高频带的增益,即LESO对系统控制输入端扰动δc具有良好的抑制能力。

针对以上结论，对参数进行了如下整定。

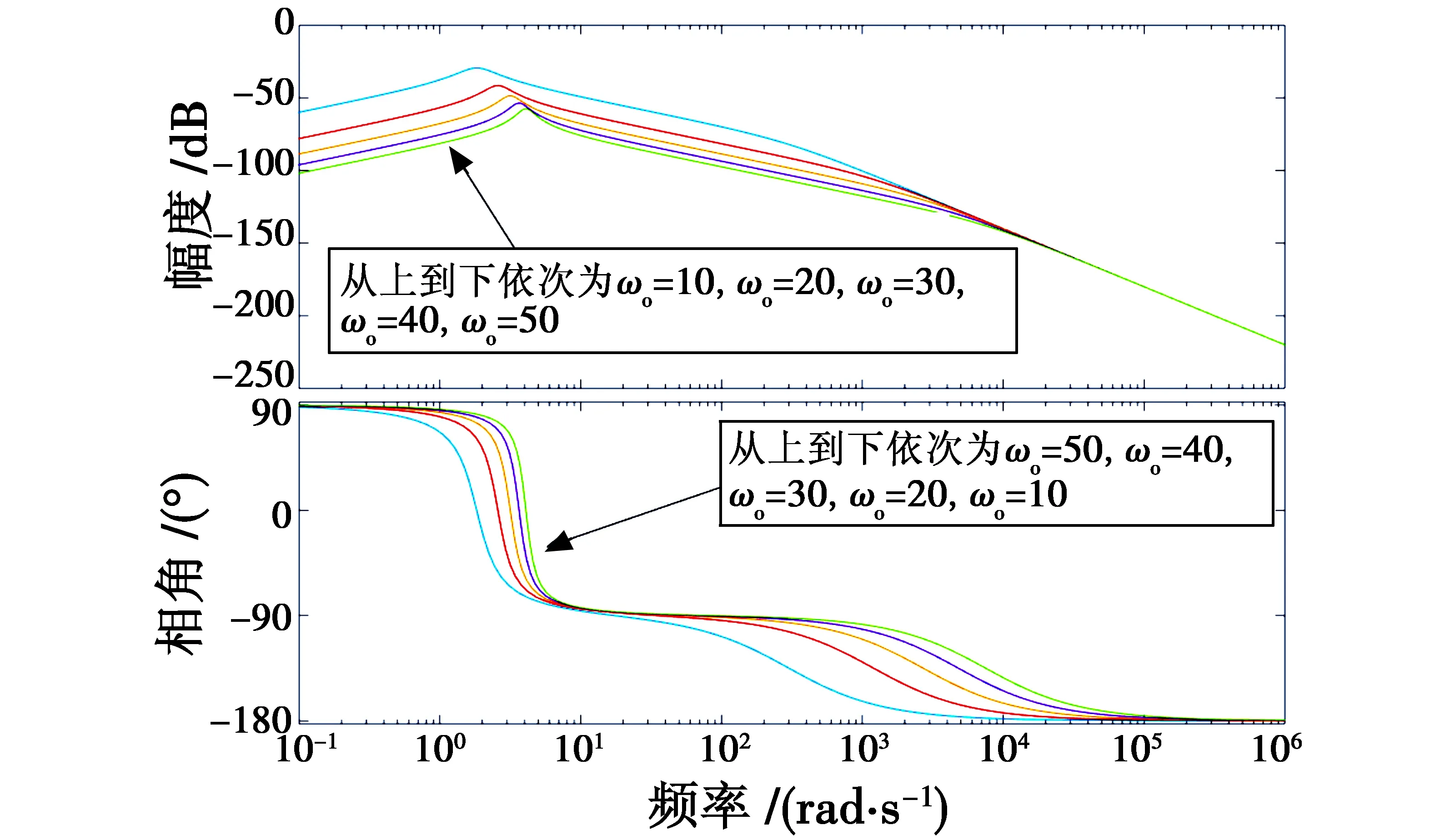
图4 输入扰动Bode图 Fig.4 Bode diagram of input disturbance

2 系统参数整定及分析

为了比对自抗扰控制器针对扰动的性能提升，针对卫星的自振动，本文在仿真中使用了一个白噪声发生器，通过图5模拟的滤波器就可以模拟噪声的干扰[9]。

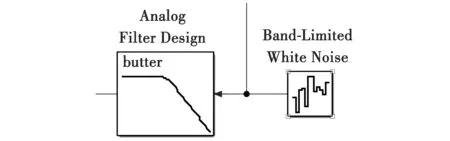
图5 噪声模拟Fig.5 Noise simulation

输出的噪声图形如图6所示。

将该模块插入系统的输出部分，并构建控制系统和控制对象。经过试验测试，精跟踪系统可以近似成一个二阶系统，相应采用三阶线性状态观测器进行观测[10]，完成后如图7所示。

针对图7控制对象进行参数整定，调节步骤如下：

1) 首先设置输入信号为一个单位阶跃信号，需要调整的参数为b0,ωc,ωo，根据系统的传递函数，将b0的值定为b0=2×107；

3) 选择ωo=ωc，对系统进行Simulink仿真，对ωo,ωc进行等量递增，直到超出系统容限(大量仿真表明，ωo和ωc之间存在一个简单的对应关系，即ωo为ωc的3～5倍)；

4) 分别增加或者减少ωo或者ωc的值，使系统达到所需性能。

图7 Simulink仿真结构Fig.7 Simulation structure of Simulink

在参数整定的过程中发现：当ωc值固定，ωo增大时(分别取值为ωo=3ωc,ωo=4ωc,ωo=5ωc)，出现了性能的改变，其性能变化如图8所示。

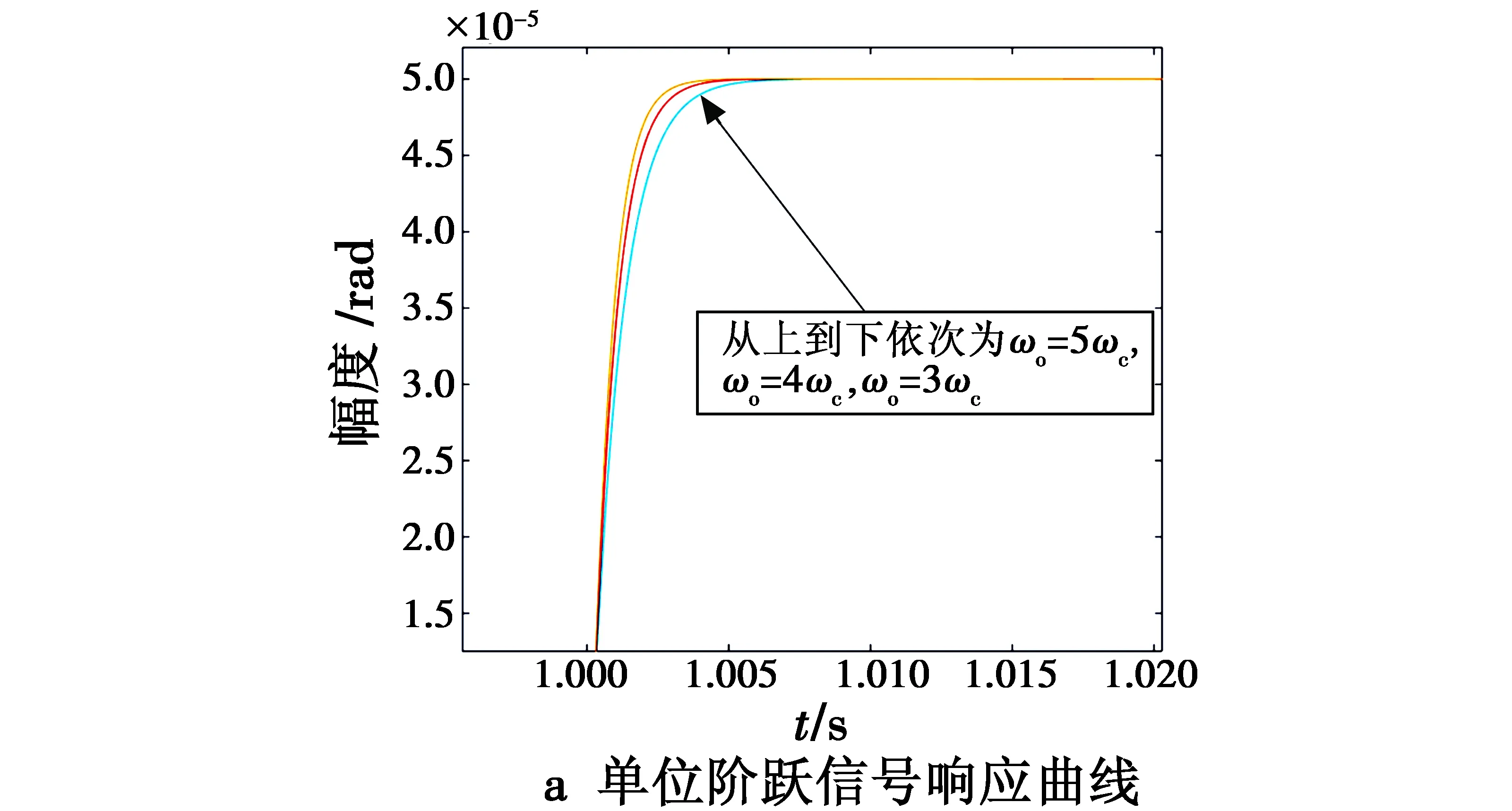
图8 单位阶跃信号下的性能变化Fig.8 Performance changes under unit step signals

如图8a所示，随着ωo的增大，系统的阶跃响应曲线的快速性得到了提高；但是系统的噪声放大作用出现了明显增大(如图8b所示)，从而对应了上文结论。所以针对系统所要求的性能对ωo进行适当增大，可以提升系统的控制精度，但是，随之而来的问题就是噪声的放大作用，所以需要在性能和噪声抑制之间找到一个合适的ωo值。

针对输入端扰动将自抗扰控制方法与传统PID控制方法做对比，图9所示为自抗扰控制方法在正弦输入分别为30 Hz，50 Hz，70 Hz，90 Hz频率下的控制误差结果。

在正弦输入分别为30 Hz，50 Hz，70 Hz，90 Hz频率下PID控制的控制误差结果如图10所示。

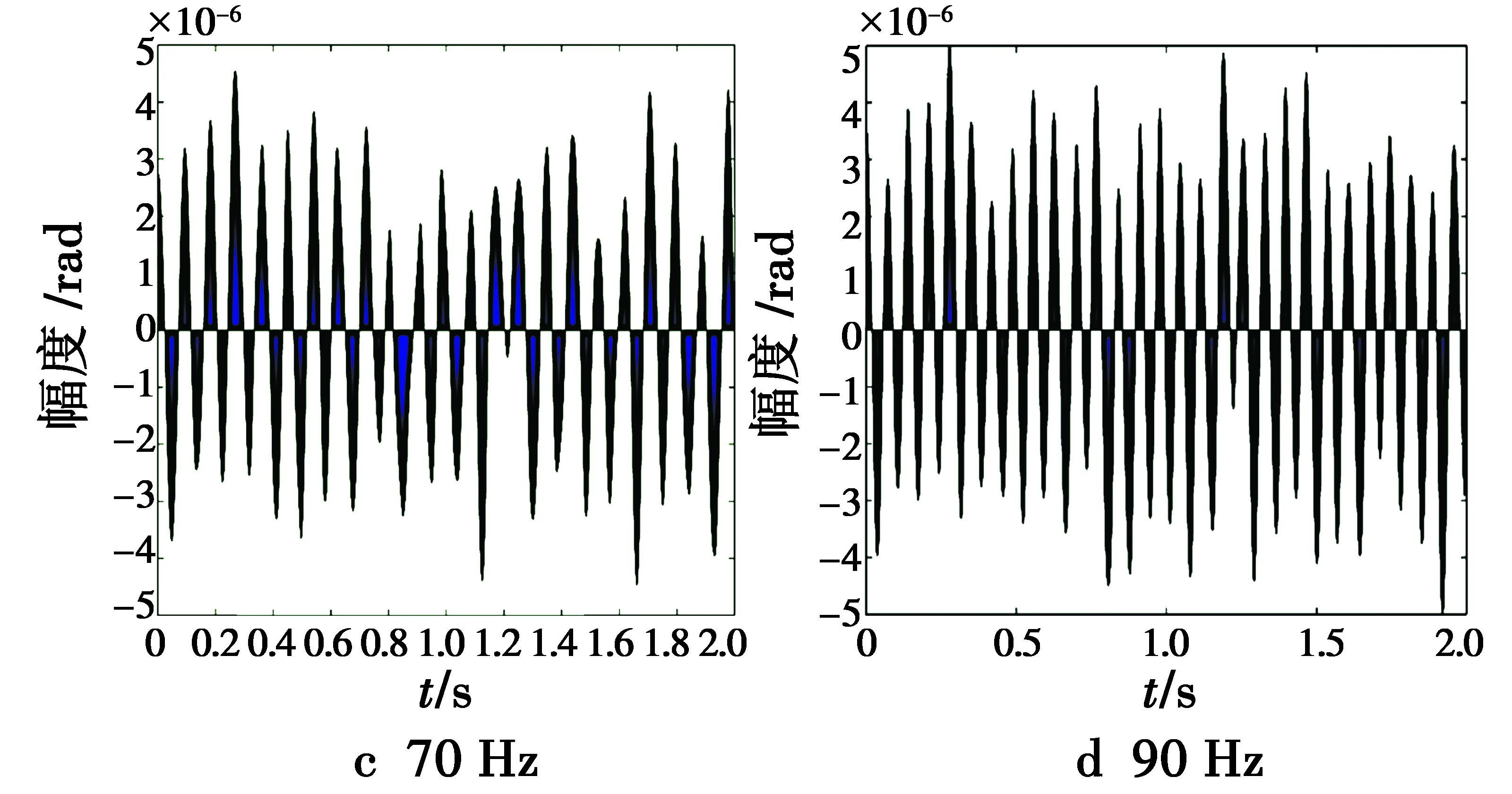
图9 ADRC控制策略在不同输入频率下的控制误差Fig.9 Control error of ADRC control strategy under different input frequencies

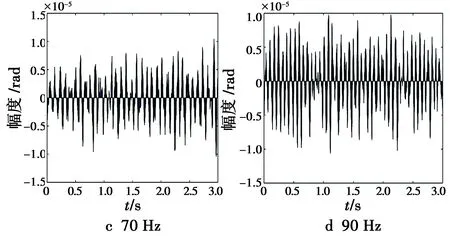
图10 PID控制方法在不同输入频率下的控制误差Fig.10 Control error of PID control method under different input frequencies

从仿真结果可以发现，在空间光通信APT系统的精跟踪部分，自抗扰控制策略相比传统的PID 控制方法具有更高的控制精度，尤其是输入频率在30 Hz时，自抗扰控制策略的精度可达3～4 μrad，而传统的PID方法误差则在8 μrad以上,可以明显看出自抗扰控制策略的优势所在。

3 总结

本文简述了线性自抗扰控制策略，并将该策略应用在空间光通信APT系统的精跟踪部分上，针对精跟踪系统的数学模型对线性自抗扰控制策略的参数进行 了一系列调整，并在加入模拟噪声后对线性自抗扰控制策略的扰动抑制做了分析和仿真。通过实验证明，自抗扰控制策略应用在空间光通信APT系统上，系统自身的噪声抑制性能有较大的提升，相比传统的PID方法,其控制精度得到了进一步提高，具有一定的实用价值。