单目视觉行人身体多部件距离融合估计算法
程 凡, 毛 琳, 杨大伟
(大连民族大学 机电工程学院,辽宁 大连 116605)
随着智能汽车的快速发展,各种汽车辅助驾驶系统应运而生[1-2],车前行人距离作为行人安全判断的重要标准之一而受到广泛关注。现今的距离估计系统大部分难以推广,距离获取速度较低,开发一种简单易行的距离估计算法已经成为了刻不容缓的课题。
目前,应用于智能交通领域的行人距离估计方法通常采用微波测距、超声波测距、激光测距、红外测距和计算机视觉等。文献[3]利用IR-UWB微波雷达系统进行测距,通过发射信号与回波信号的时间差对距离进行估计,但该算法耗时较长,算法稳定性较低;文献[4]对原有超声波测距算法进行了改进,提升超声波频率,扩大采样范围,并通过提升算法复杂度降低了对硬件的需求,但由于超声波的传播速度较慢,无法保证算法的实时性;文献[5]使用激光测距系统与集光定位系统两部分共同完成距离估计,系统距离估计结果精准,但对环境与使用设备要求高,难以广泛推广;文献[6]中通过设置多个红外发射接收器对距离进行估计,展现出了良好的实用性,造价低,反应速度快,但仅可应用于小范围。机器视觉测距主要分为单目视觉测距与双目视觉测距两种方式。文献[7]通过分析摄像头内部参数并将参数分解为两个线性方程组,以数学的方式对距离进行估计,降低了算法复杂度;文献[8]将双目立体视觉与红外测距相融合,通过红外测距法弥补了双目立体视觉在距离估计范围方面的不足。
本文提出一种基于单目视觉的行人身体多部件距离融合估计算法(M2DEA),对图像中的信息进行提取[9],在仅以单目摄像头作为图像获取设备的前提下,利用行人身体特征进行距离估计。本算法分别通过图像中车前行人脚部件及头部件像素高度估计距离,利用脚部件半水波形等距线及头部件高度插值距离估计算法,融合两种身体部件距离估计结果,避免了在复杂街道环境中行人身体部分被遮挡而无法实现距离估计的情况[10],增强了算法的稳定性。
1 M2DEA算法
M2DEA算法以单目摄像头作为图像采集设备,利用不同身体部件特征进行车前行人距离估计,逻辑图如图1。图像输入后首先通过两点法校正,建立图像坐标系与世界坐标系的联系,之后将校正后图像作为输入获取行人的脚、头部件,通过在线距离估计与离线模型标定两部分,以线性最小方差为准则进行融合得到估计结果。

图1 M2DEA算法逻辑图
1.1 两点法校正
摄像头在固定时由于环境等因素难以保证角度水平,造成了世界坐标系与图像坐标系转换的偏差,通过两点法对图像进行校准。
在摄像头位置固定后,垂直于地面且经过相机镜头光轴所在直线建立XOY平面,取一垂直于OY的直线L1L2;在L1L2上任取两点D1、D2,D1、D2两点应在摄像头可视范围内。标定场景示意图如图2。D1D2在实际场景中处于水平,故校准后两点在图像中仍应处于水平线上,通过角度偏转、图像平移两步实现D1D2在图像中的水平关系。

图2 标定场景示意图
采用两点法对摄像头获取的图像进行校准,建立了实际场景与图像之间的联系,通过对场景中对应点的标记实现世界坐标系与图像坐标系的转换,保证了后续算法对图像深度信息挖掘的准确性。
1.2 半水波形等距线距离估计算法
半水波形等距线距离估计算法主要利用车前行人脚部像素位置作为特征对距离进行估计。根据多次实验结果可以得出,行人脚部件位置与距离之间满足一定的对应关系,且与摄像头距离相同但位置不同的行人脚部像素位置呈水波形分布,故而提出半水波形等距线距离估计算法。经多场景仿真测试,车前行人脚部件像素坐标由相机摆放位置与行人距离共同决定,在道路平缓情况下,不受其他环境因素影响。故当相机摆放位置固定时,车前行人脚部件像素坐标将对应唯一距离,通过线下生成二者对应关系完成离线模型标定过程,在线完成实时距离估计。
半水波形等距线距离估计算法主要分为离线模型标定与在线距离估计两部分。通过在实际场景中采集图片,获取行人脚部像素坐标与距离的对应关系完成离线模型标定过程。在离线模型标定过程中,需通过校正使得图像坐标系符合世界坐标系准则。建立半水波形等距线模型,完成离线模型标定过程。在线距离估计中,通过能量滤波算法获取待测图像中行人脚部像素坐标,作为半水波形等距线距离估计法的输入得到估计距离。
在离线模型标定过程中,以ri(i=1,2,3, ...,n)为等距线半径得到采集点,采集点数量为n(n∈Z+)。采集工作在图像左侧完成,等距线关于x=0.5·lx对称,lx为图像宽度,右侧采集点通过左侧点映射获取。通过曲线拟合建立ri条等距线。拟合曲线如图3。

图3 半水波形等距线模型
曲线拟合方法采用最小二乘法,等距线方程为

i=1,2,3, ...,n。
(1)
式中:ai,bi和ci为曲线拟合系数;xi和yi为图像。像素坐标系坐标位置。同时,存在一条过原点O和A点的一次直线函数:
yi=k·xi,i=1,2,3, ...,n。
(2)
将公式(1)和(2)联立方程组,求出直线OA与全部等距线在第I象限的交点坐标:
(3)
(4)
行人脚部部件A点到原点O的像素距离点集为
(5)
对所得距离点集P中各元素应用公式(6)插值,得出相对应的一组行人目标距离测量值d的对应关系。
1.3 头部件高度插值距离估计算法
头部件高度插值距离估计算法依靠头部作为刚性部件的高度特征不变性对距离进行估计。算法主要分为离线模型标定与在线距离估计两部分。通过实验图像获取头部像素高度与距离之间的对应关系,提出刚性部件尺寸-距离插值法,完成离线模型标定过程。在线距离估计中,通过超像素分割算法对图像进行处理,获得头部像素高度后,经刚性部件尺寸-距离插值法获取距离估计结果。头部像素高度与距离对应关系如图4,横轴为头部的像素高度,纵轴为行人目标与摄像头之间的相对距离。

图4 头部件像素高度与相对距离关系
头部像素高度与相对距离之间存在对应关系,故对距离的获取主要依赖于行人头部高度。在街道场景中,由于背景过于复杂,行人头部高度难以获取,为解决该问题,本文采用超像素分割算法[11]来完成目标行人头部与背景的区分。首先通过DPM模型[12]检测行人并划分出头部区域,超像素算法仅针对头部区域内图像进行处理,在去除头部冗余像素的同时避免了实时性低的问题。头部件高度获取示意图如图5。

图5 头部件高度获取示意图
以O为端点任取一条射线OZ,并在该射线取n个标定点,令行人目标站在标定点上,对n个行人目标通过超像素算法对头部高度hn进行计算,利用Lagrange插值求取头部高度-距离的关系。设n个头部高度插值节点为p,相对应的一组行人目标距离的地标点测量值d,头部高度和距离的对应关系即为求一个插值多项式H,满足
(6)

1.4 多部件融合算法
本文并行处理相对独立的头部件与脚部件进行距离估计,两种算法互相校验保证了算法的可靠性。同时,在人车混行的复杂环境中,身体部分部件极易被遮挡,通过不同身体部件进行距离估计,降低了算法失效的可能性。算法通过线性最小方差融合准则进行,只需计算加权系数,减小了计算负担。
融合算法具体实施步骤如下:
(1)获取距离估计结果。利用半水波形等距线距离估计算法及头部件高度插值距离估计算法分别对同一位置上的行人进行距离估计,获取两组等精度距离估计值。
(2)获取标准差。利用等精度数据判断两种方法的稳定程度,得出具体的标准差。由于单次测量精度相同,故其标准差均为σ。
(3)获取权重。为保证算法稳定性,融合权重系数主要以标准差为依据进行判断。给定基于头部与脚部的测距算法所占权重分别为p1、p2,则各组算术平均值的标准差为
(7)
(4)获取融合距离估计值。通过融合算法得出距离估计值D,头部部件距离DH,脚部部件距离DF。
D=p1DH+p2DF。
(8)
2 仿真分析
仿真实验在Matlab R2014a和Windows 7操作系统下进行。图像以单目摄像头作为图像采集设备,镜头中心与地面距离为1.4 m,符合大多数车辆车载摄像头高度,仿真在目标行人距离摄像头5~35 m范围内完成。仿真在非遮挡条件与半遮挡条件两种情况下进行,当身体部件被半遮挡时,可通过未被遮挡单一部件进行距离估计。
2.1 非遮挡条件下仿真

累积误差曲线如图6,横坐标为测量距离,纵坐标为累积误差。融合后累积误差低于单一算法的累积误差值,该融合算法在距离估计准确程度上优于单一算法。

表1 身体多部件融合距离估计算法仿真结果
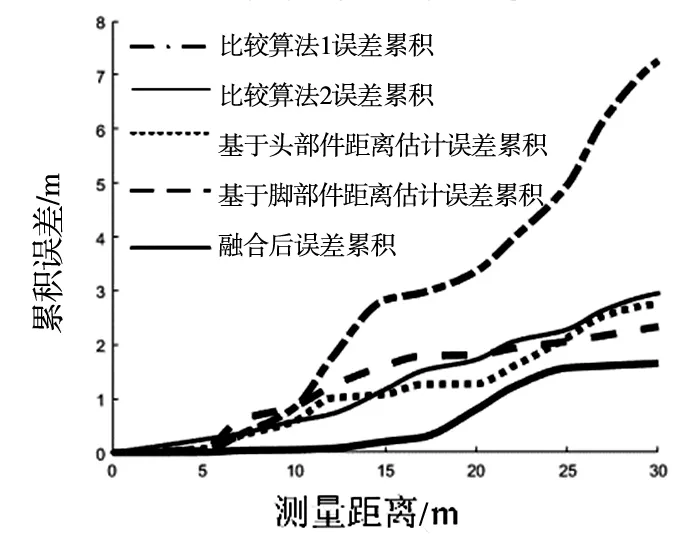
图6 累积误差曲线
仿真场景1、2在街道中进行拍摄的结果如图7。令五名目标行人分别采取在路边玩手机、面向摄像头行走、横穿斑马线及横穿车前的姿态。仿真场景2中令四名目标行人采取面向车辆行走、从障碍物后走出、横穿车辆前及背离车辆行走的姿态。
2.2 半遮挡条件下仿真
在半遮挡情况下,采集路障后与行车路中间两个场景对单一行人进行距离估计。在第一个场景中,行人脚部被路障遮挡,在第二个场景中,行人头部被障碍物遮挡。仿真结果表明,本文提出算法在行人身体被部分遮挡的情况下,仍能输出目标行人与摄像头之间的有效距离,确保本算法在智能汽车及行人危险预判等方面的应用。

(a)仿真场景1 (b)仿真场景2

图8 身体部件遮挡后距离估计
3 结 论
针对人车混行复杂环境中,自主汽车辅助驾驶系统对车前行人距离估计的问题,提出了单目视觉的行人身体多部件距离融合估计算法。依据行人身体特征进行距离估计,分别通过脚、头部件构建半水波形等距线距离估计模型及刚性部件尺寸-距离插值模型。经仿真验证,本算法距离估计结果在35 m距离估计范围中,误差在1 m以内。同时,在行人身体被半遮挡的情况下能够对行人进行有效的距离估计,在35 m范围内,可将误差控制在2 m以内。本算法能够为行人危险判断提供有效的数据支撑,在智能汽车、无人车等研究领域中具有较强的应用价值。

