一类非线性系统基于LS-SVM的自适应滑模控制

谢春利，赵丹丹

(大连民族大学 a.机电工程学院；b.计算机科学与工程学院，辽宁 大连 116605)

非线性不确定系统的滑模变结构控制一直是控制界关注的热点，很多学者在此领域取得了研究成果[1-2]。由于非线性系统的滑模控制需要已知系统的粗略数学模型，因此增加了滑模控制对系统模型的依赖。随着人工智能理论的发展，模糊逻辑和神经网络被引入滑模控制设计中来，有效地减少了滑模控制对系统模型的依赖[3-4]。文献[3]研究了基于高增益观测器的非线性系统自适应模糊滑模控制，文献[4]研究了基于神经网络的非线性系统自适应滑模控制，它们主要是利用模糊逻辑或神经网络对任意非线性逼近的能力。但是，模糊逻辑和神经网络应用中存在算法复杂、学习速度慢等问题，而最小二乘支持向量机[5](Least Squares Support Vector Machines，LS-SVM)解决了上述问题。LS-SVM保持了标准SVM的强大泛化和全局最优能力，极大地提高了训练效率，同时基于LS-SVM的非线性系统控制研究取得了丰富成果[6-10]。但是，将LS-SVM和滑模变结构控制相结合的非线性不确定系统分析和设计的方法则相对较少。

本文针对一类包含不确定性和未知有界外部干扰的非线性系统，提出了一种基于李雅普诺夫(Lyapunov)函数的自适应滑模控制方法。该方法充分利用LS-SVM回归的非线性函数逼近能力设计反馈线性化控制器，引入滑模控制补偿LS-SVM回归的逼近误差及不确定外部干扰对系统输出的影响，利用Lyapunov函数进行LS-SVM权值参数的调整，最后通过一个仿真实例对设计方案进行了验证。

1 问题描述

考虑非线性不确定系统

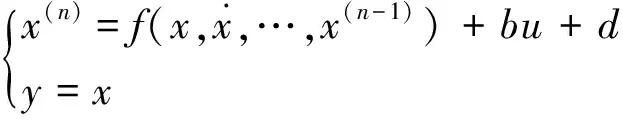
(1)

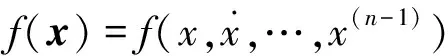
控制目标就是基于LS-SVM回归实现状态反馈控制u=u(x,θ)，以便保证闭环系统一致有界，跟踪误差小。为了实现目标，给出如下假设：

假设1.2 控制增益b满足b≥bL>0，bL为b的下界。干扰d有界，假设其上界为D，即|d|≤D，给定D>0。

如果函数f(x)已知且干扰d=0，则状态反馈控制器为

(2)

由式(1)和式(2)计算得到

e(n)+kne(n-1)+…+k1e=0 。

(3)

式(3)表明，通过适当选择ki(i=1,2,…,n)，就能保证sn+knsn-1+…+k1=0的所有根都在复平面左半平面，即limt→∞e1(t)=0。

2 基于LS-SVM回归的自适应律设计

LS-SVM将最小二乘线性系统引入SVM，代替传统的支持向量采用二次规划方法求解分类和函数估计问题，算法的推导参见文献[5]。

用于逼近控制器的LS-SVM回归结构参见文献[10]，其输入输出关系为

u(x,θ)=θTβ。

(4)

设理想的权值参数向量为

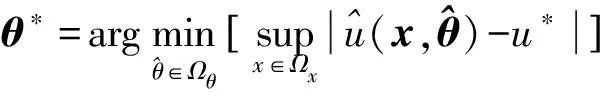
(5)

u*=u(x,θ*)+ε(x),x∈Ωx⊂Rn。

(6)

式中，ε(x)为LS-SVM的逼近误差，对任意的常数Δε>0，满足|ε(x)|≤Δε。

定义滑模面为

s=KTe。

(7)

其中kn=1，则

=b(u*-u)-d。

(8)

根据式(6)，设计滑模控制器为

(9)

式中，

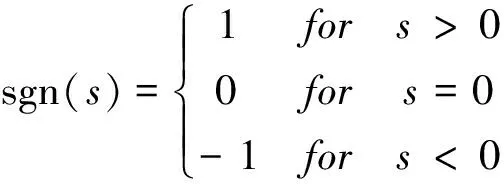
(10)

取

δ(t) =max|d/b|+η,η>0

=D/b+η；

(11)

取权值参数向量的自适应律为

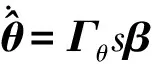
(12)

式中，Γθ>0是设计参数。

定理对于式(1)描述的非线性不确定系统，采用文献[10]中的LS-SVM结构逼近式(2)中的u*，控制量取为式(9)，权值参数向量自适应律为式(12)，则闭环系统内所有信号有界。

证明：选择如下Lyapunov函数

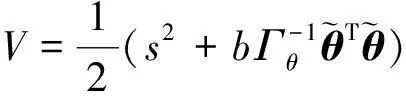
(13)

令V对时间求导数有

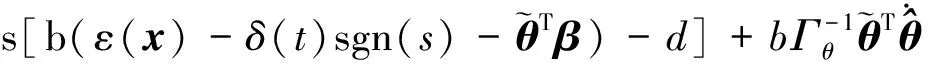
=s[bε(x)-bδ(t)sgn(s)-d]+

(14)

由式(12)可得

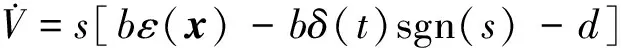
(15)

取η>Δε>0，利用式(11)可得

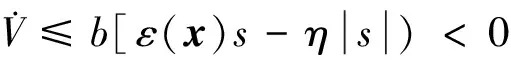
(16)

可知闭环系统是渐近稳定的。

3 仿真研究

考虑非线性不确定系统

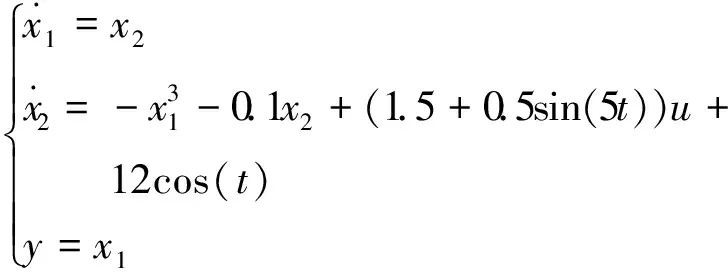
(17)

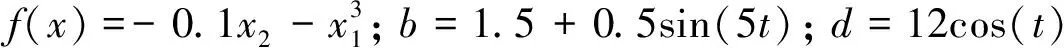
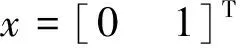
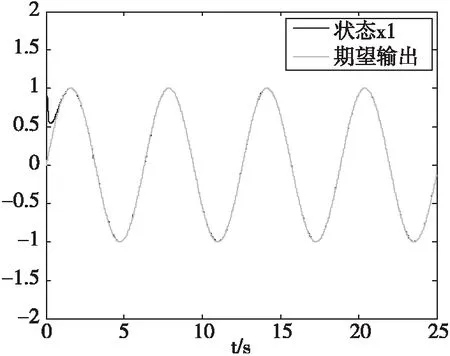
图1 状态x1及期望输出

图2 状态x2及期望输出

图3 控制输入

然后实现基于神经网络的自适应滑模控制。神经网络控制器结构和参数选取参考文献[11]。基于神经网络的自适应滑模控制的仿真结果如图4、图5和图6。其中，两种控制方法的跟踪误差曲线如图7。对比跟踪误差曲线可知，基于LS-SVM方法的误差平均值为-0.009 3，基于神经网络方法的误差平均值为-0.020 7，表明本文控制方法控制精度更高。

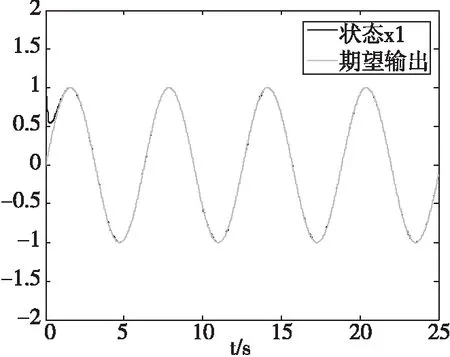
图4 状态x1及期望输出

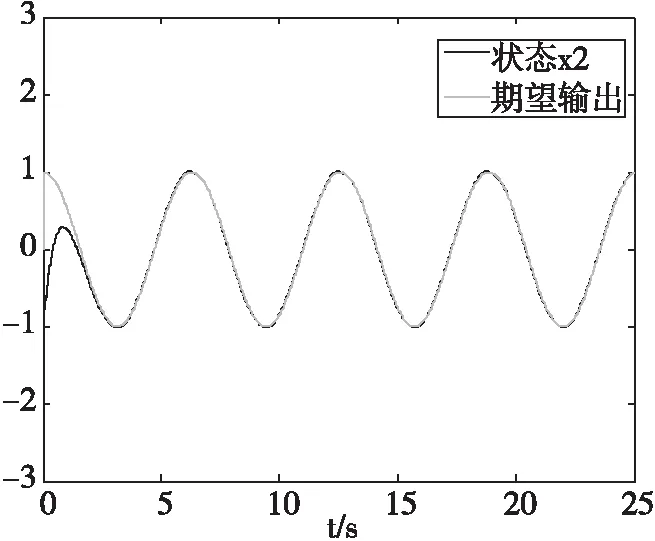
图5 状态x2及期望输出

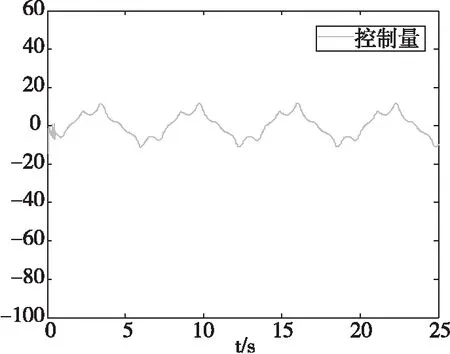
图6 控制输入

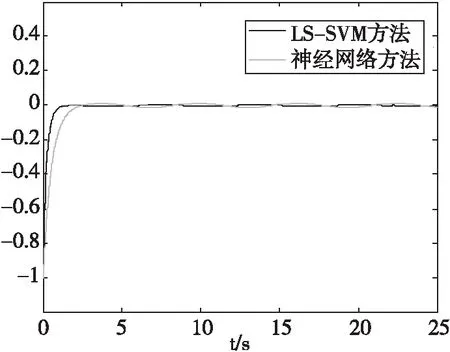
图7 跟踪误差

4 结 论

本文研究了基于LS-SVM回归的一类单输入单输出非线性不确定系统的自适应滑模控制问题。在控制系统的设计中，利用非线性系统的反馈线性化技术和LS-SVM回归的任意非线性函数逼近能力构造反馈控制器，通过滑模控制技术来提高控制系统的鲁棒性，并证明了所提控制方案可以保证闭环控制系统渐近稳定。仿真结果验证了该方法的有效性。