南海西部低渗油藏水平井非稳态产能评价方法*

雷 霄 王世朝 焦青琼 张乔良 王雯娟 马 帅

(1. 中海石油(中国)有限公司湛江分公司 广东湛江 524057； 2. 中海油能源发展股份有限公司工程技术公司 广东湛江 524057)

南海西部低渗油藏具有较大的开发潜力，是未来增储上产的主力之一，但储层厚度较薄，储量难动用，多采用长水平段裸眼水平井依靠弱天然能量或后期注水开发,且水平井投产后产能下降较快，初产及中后期稳产差异大，处于不稳定渗流状态。低渗油藏物性较差，存在启动压力梯度、应力敏感等非达西渗流特征[1-3]，但目前的研究大多仅考虑了启动压力梯度或应力敏感效应[4-6]，同时考虑这两个参数对水平井产能影响的研究较少[7]。另外，水平井非稳态产能研究多以椭球流[8-11]为主，但对于储层厚度较薄的油藏产能计算误差较大，椭圆流则更加适用于描述薄层油藏水平井的流动形态。对于存在不渗透边界(如断层)的油藏，受不渗透边界的遮挡影响，渗流范围减小，导致产能在自然递减的基础上进一步降低。因此，亟待建立一种适应于海上低渗薄层油藏以及断块油藏水平井非稳态产能评价方法，同时分析非达西渗流对产能的影响程度，为制定高效合理的开发方案提供依据。

1 模型建立

1.1 水平无限大储层水平井非稳态产能模型建立

假设无限大油藏一口水平井位于油藏平面中心，水平段延展方向与x轴平行，平面渗流形态呈一个椭圆形(图1)。

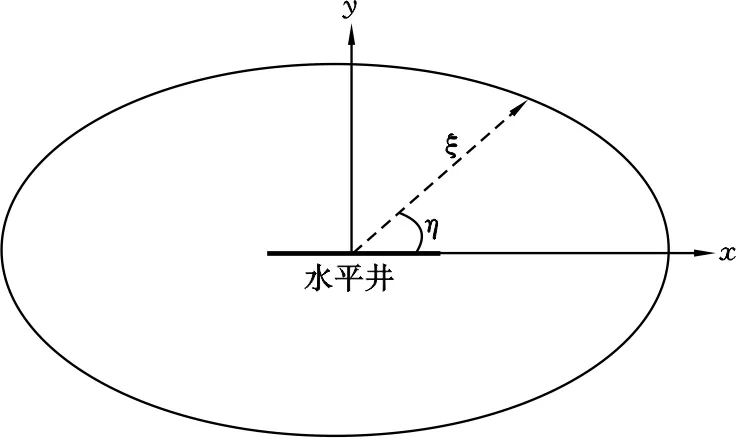
图1 无限大油藏一口水平井平面渗流形态示意图Fig .1 Schematic map of flow pattern in the horizontal dimension for one single horizontal well at infinite oil reservoir

图1中直角坐标(x，y)与椭圆坐标(ξ，η)的变换关系如下：

(1)

式(1)中：a为椭圆长轴半长;b为椭圆短轴半长;L为水平段长度半长。

水平井水平段半长与储层厚度的比值L/h≫3时，水平井产能可近似为裂缝垂向上完全贯穿储层时的压裂直井产能[12]。文献[13]在此基础上建立了相应的油单相非达西非稳态渗流数学表达式，然而在推导过程中只考虑了水平方向渗流的阻力，忽略了垂向渗流时的阻力和井附近储层污染的影响，导致当水平方向渗透率与垂直方向渗透率比值较大时计算的水平井产能明显偏高。为了更加全面地描述水平井在水平、垂直方向上的流动，并考虑各向异性的影响，需要对水平方向单相非达西非稳态渗流解析式进行校正，在借鉴前人对水平井垂向阻力和表皮因子研究成果[13-16]基础上，引入垂向阻力和表皮因子附加项(式(2))，得到水平井采油指数((式3))和无因次时间((式4))。

(2)

(3)

(4)

式(2)～(4)中：Kh为水平方向渗透率，mD；Kv为垂直方向渗透率，mD；h为储层厚度，m；rwe为有效井筒半径，m;μ为原油黏度，mPa·s；pw为井底压力，MPa；pi为地层原始压力，MPa；ξR为外边界椭圆坐标；ξw为内边界椭圆坐标；rw为井筒半径，m；tD为无因次时间；s为表皮系数；q为日产油量，m3/d。

内边界椭圆坐标ξw可由式(5)计算得到[9],即

(5)

由式(4)可以看出，由无因次时间去计算外边界椭圆坐标ξR是困难的。因此，在实际计算非稳态产能的过程中，首先给定不断变化的外边界椭圆坐标ξR，根据式(4)计算得到无因次时间tD，结合无因次时间定义式(式(6))与无因次启动压力梯度定义式(式(7))，即可计算出ξR对应的生产时间t。

tD=Kht/(φμCtL2)

(6)

GD=4GKhLh/(qμB)

(7)

式(6)、(7)中：t为时间，s；φ为孔隙度，f；Ct为综合压缩系数，MPa-1；G为启动压力梯度，MPa/m；B为原油体积系数，m3/m3。

根据式(3)可以计算得到ξR对应的采油指数J，从而建立采油指数J与生产时间t之间的关系。

若不考虑启动压力梯度与应力敏感，则式(3)、(4)可分别转化为常规达西渗流条件下水平井采油指数与无因次时间计算式,即

(8)

-1]

(9)

1.2 不同垂直相交不渗透边界对产能的影响

对于水平无限大均质油藏中1口直井，有

(10)

式(10)中：Φe为供给边缘对应的势；Φw为内边界对应的势；Re为供给边缘半径，m。

当水平方向不是无限大，存在1条不渗透边界时，这时不渗透边界起分流线作用(图2)，依据镜像反映与势的叠加原理，地层中任一点M的压降应为各井单独工作时对M点引起的压降的总和，通常取油井所在区域中心至供给边缘的半径作为各井共同的供给边缘半径Re[17]，有

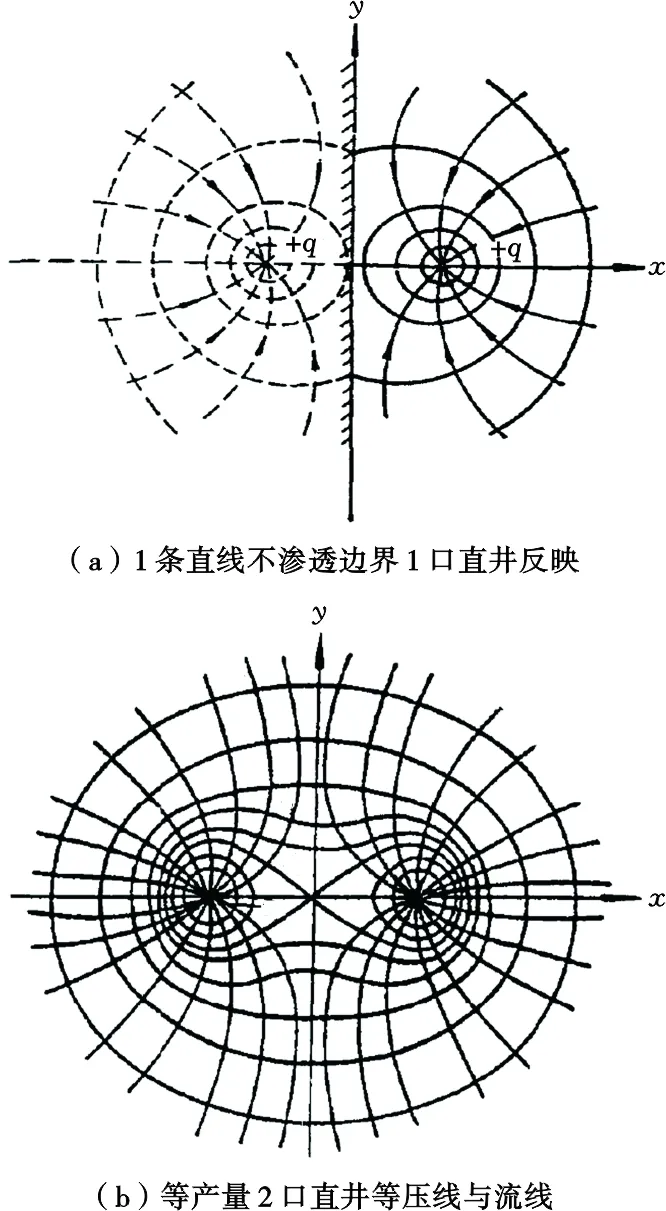
图2 直线不渗透边界起分流线作用示意图Fig .2 Schematic diagram of straight impermeable boundary acting as diverting stream line

(11)

式(11)中：qi′为第i井考虑不渗透边界时产油量，m3/d；ri为第i井到M点的距离，m。

当井落于不渗透边界上，有

(12)

由于等产量2口井落于同一点时的压力场与无限大1口井(产量为前者之和)的压力场分布是相同的，从而得到产能关系如下：

(13)

式(13)中：J为不考虑不渗透边界时产能，m3/(d·MPa)；J′为考虑不渗透边界时产能，m3/(d·MPa);pe为供给边缘处压力，MPa。

若井与不渗透边界存在一定的距离，随着生产的进行，远离不渗透边界一侧的供给比例逐渐增大，到一定程度时泄油面积可近似取1/2，此时有

(14)

同理，当井落于2条垂直相交的不渗透边界交点上，依据镜像反映与势的叠加原理，有

(15)

从而得到产能关系为

(16)

若井与2条不渗透边界存在一定的距离(图3)，随着生产的进行，远离不渗透边界方向的供给比例逐渐增大，到一定程度时泄油面积可近似取1/4，此时有

(17)

同理，可得存在3条、4条垂直相交的不渗透边界时的产能校正系数(表1)。

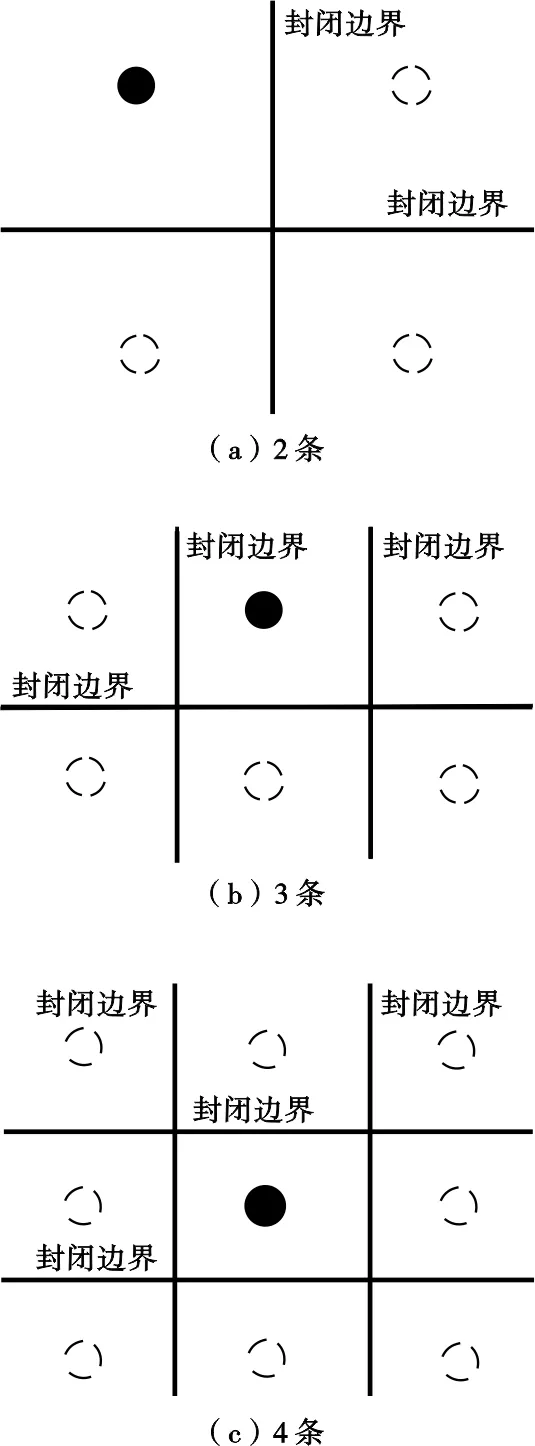
图3 不同垂直相交的不渗透边界示意图Fig .3 Schematic diagram of different perpendicularly intersect closed boundaries表1 垂直相交不渗透边界与产能校正系数的关系Table 1 Relationship between productivity correction coefficients and perpendicularly intersect impermeable boundaries

垂直相交不渗透边界(条)产能校正系数11/221/431/641/9

虽然水平井、直井分别是线源、点源模型，但不渗透边界对水平井、直井产能的影响并没有本质的差别，如文献[18]中提及1条不渗透边界时水平井产能校正系数同样为1/2，表1中垂直相交不渗透边界与产能校正系数的关系同样适用于水平井。

2 实例验证

2.1 不渗透边界影响不明显时低渗水平井产能评价

南海西部珠江口盆地文昌M区X1油组属于低渗砂岩油藏，以粉砂岩、泥质粉砂岩为主，喉道为缩颈喉道，喉道较小使得储层孔隙较大但渗透性差。文昌D油田X1油组为弱边水驱动构造油藏，沉积储层多为浅海席状砂，颗粒细，测井渗透率平均为17.8 mD，孔隙度平均为21.3%。文昌E油田X1油组为边水驱动构造油藏，沉积储层多为浅海水下浅滩粉砂岩，颗粒细，测井渗透率平均为23.0 mD，孔隙度平均为24.3%。文昌F油田南块X1油组为弱边水驱动岩性油藏，沉积储层多为滨外砂坝，测井渗透率平均为16.8 mD，孔隙度平均为24.3%。

以文昌M区X1油组3口水平井作为研究对象，综合压力恢复稳态测压法[19]、岩心应力敏感试验(定围压、变内压)以及低渗试井解释[12]等3种方法，得到相应的启动压力梯度、应力敏感系数(见表2)。从表2可以看出，与常规试井模型相比，低渗试井模型解释渗透率均有小幅增加。低渗试井模型解释的启动压力梯度、应力敏感系数与压力恢复稳态测压法、岩心应力敏感试验计算结果接近。考虑到低渗透油藏水平井试井模型[13]可同时获得启动压力梯度、应力敏感系数以及测试井附近渗透率数值，并且更加全面描述储层特性，因此优先选择低渗试井模型解释结果作为产能计算的基础参数。

从表2还可以看出，3个油田非达西渗流特征由强到弱排序为：文昌D>文昌F>文昌E，这与“渗透率越低，非达西渗流特征越强”的认识相符。

以常规试井与低渗试井模型解释参数(表2)为基础，相应计算的达西、非达西非稳态产能与实测值对比如图4所示。若忽略垂向渗流阻力，在Kh/Kv较大时计算的水平井产能较实测产能明显偏高(图4a、b)。若考虑垂向渗流阻力，非达西渗流模型(式(3)、(4))计算的产能较常规产能模型(式(8)、 (9))略低3%～6%，但二者与实测数值均非常接近，总体误差较小(图4c)，因此可采用常规产能模型快速评价水平井非稳态产能变化规律。

表2 珠江口盆地文昌M区X1油组非达西渗流参数评价Table 2 Evaluation of non-Darcy flow parameters of X1 oil group in M block, WC oilfield,Pearl River Mouth basin

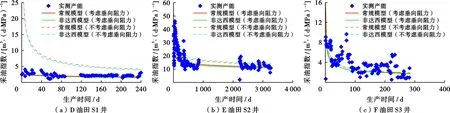
图4 珠江口盆地文昌M区X1油组3口井计算产能与实测产能对比Fig .4 Comparison between calculated productivity and tested productivity for 3 wells in X1 oil group, M block WC oilfield,Pear River Mouth basin

2.2 不渗透边界影响明显时低渗水平井产能评价

北部湾盆地涠洲油田群低渗油藏多为小断块油藏，实际应用常规产能模型(式(8)、(9))发现，若不考虑不渗透边界对水平井非稳态产能的影响，即水平无限大、自然递减状态下计算产能与实测产能相差很大；若考虑不渗透边界对产能的影响，校正后计算产能与实测产能十分接近(图5)，其中G油田W1井单采X2油组，1条不渗透断层边界；H油田W2井单采X3油组，2条不渗透断层边界；J油田X4油组为异常高压储层，原始压力系数1.36，W3井单采该油组，3条不渗透断层边界。

K油田Y1井区W4井钻后认为该井吸水能力低，与Y1井井间连通性差，无法形成有效注采，注水未抵消不渗透边界对产能的影响(图6)。M油田X7油组Z5井注水后，W5井产能部分恢复(图7)，这表明在采油井与不渗透断层之间部署注水井，在注水受效的情况下可以一定程度抵消不渗透边界对产能的影响。W1—W5井基础参数见表3。

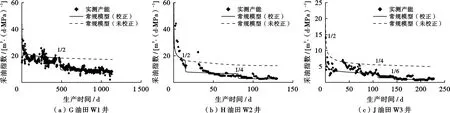
图5 涠洲油田群3口井常规达西模型校正产能与实测产能对比Fig .5 Comparison between corrected productivity and tested productivity for 3 wells in WZ oilfield group

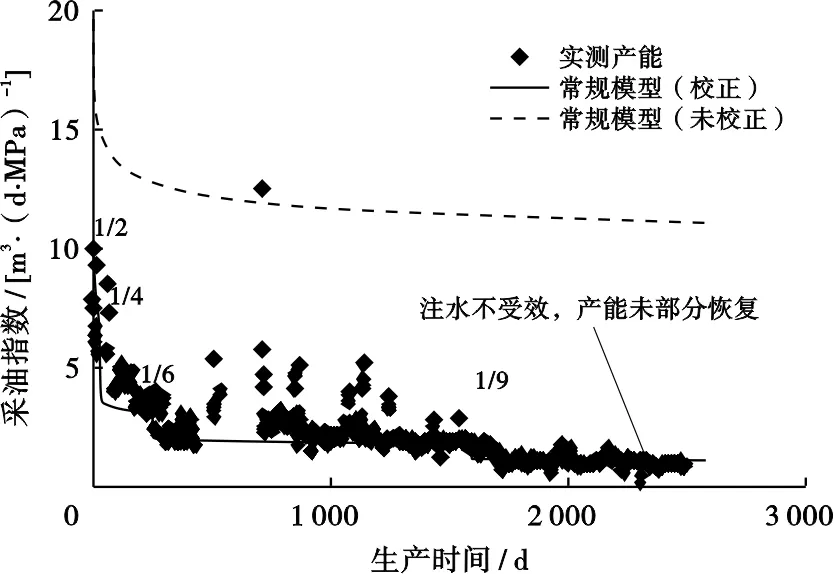
图6 涠洲油田群K油田W4井常规达西模型 校正产能与实测产能对比Fig .6 Comparison between corrected productivity and tested productivity for Well W4 in K oilfield,WZ oilfield group

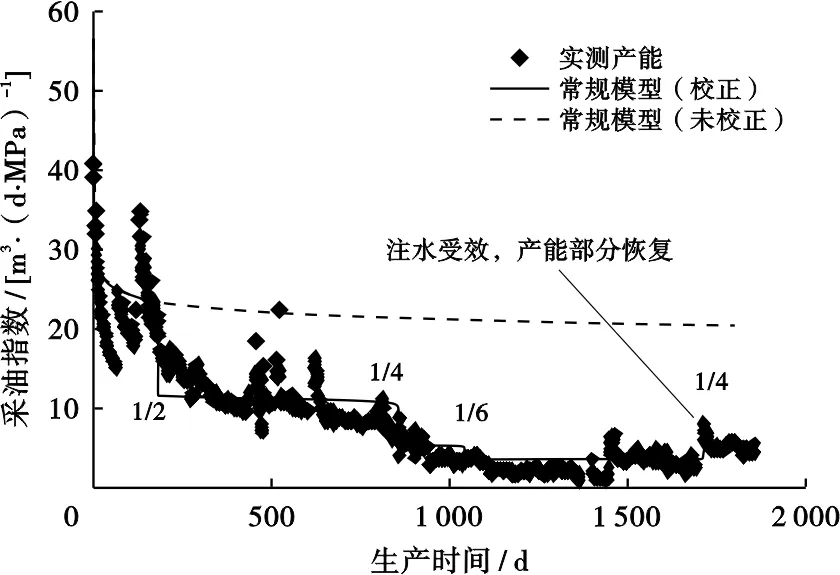
图7 涠洲油田群M油田W5井常规达西模型 校正产能与实测产能对比Fig .7 Comparison between corrected productivity and tested productivity for Well W5 in M oilfield, WZ oilfield group表3 涠洲油田群W1—W5井基础参数Table 3 Basic parameters of wells W1—W5 in WZ oilfield group

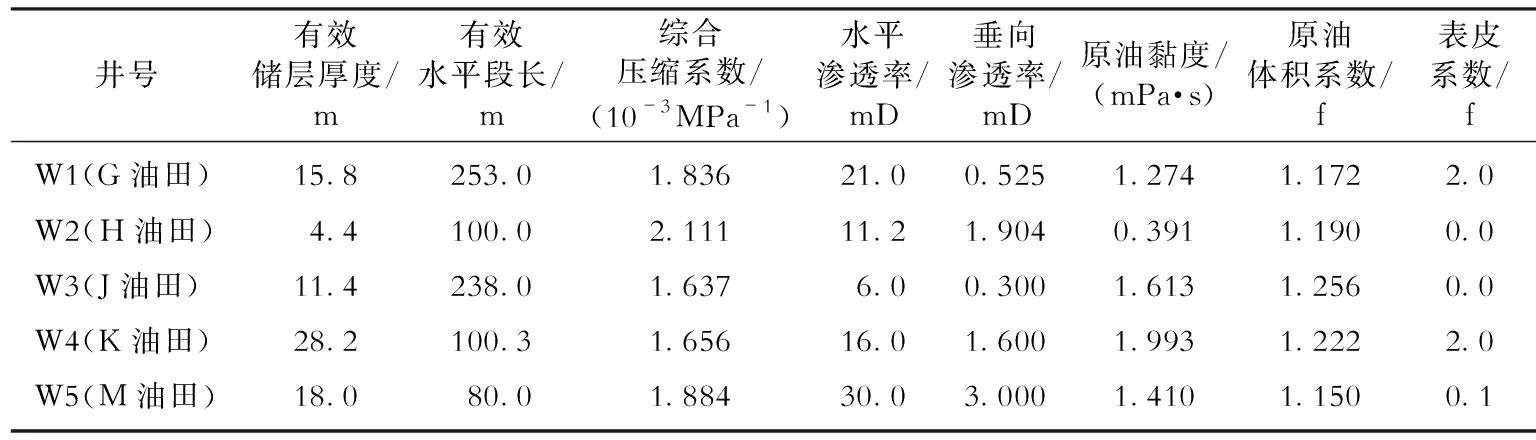
井号有效储层厚度/m有效水平段长/m综合压缩系数/(10-3MPa-1)水平渗透率/mD垂向渗透率/mD原油黏度/(mPa·s)原油体积系数/f表皮系数/fW1(G油田)15.8253.01.83621.00.5251.2741.1722.0W2(H油田)4.4100.02.11111.21.9040.3911.1900.0W3(J油田)11.4238.01.6376.00.3001.6131.2560.0W4(K油田)28.2100.31.65616.01.6001.9931.2222.0W5(M油田)18.080.01.88430.03.0001.4101.1500.1

从图5～7可以看出，水平井产能阶梯状的变化不一定是外围物性或近井污染变化引起的，有可能是附近存在不渗透或部分连通的断层、砂体不连通或连通性差、外围注水引起的。在动态监测方面，常采用干扰试井的手段评价低渗油藏断层的封堵性和储层的连通性，但耗时长、成本高、监测的范围有限。从长期生产动态上分析水平井产能阶梯状的变化趋势，耗时短、成本低、监测的范围广，有助于辅助认识断层的封堵性、砂体间的连通性以及注水有效性。

3 结论

1) 对于南海西部不渗透边界影响不明显的低渗砂岩油藏，本文建立的水平井非达西渗流模型较常规产能模型计算的非稳态产能低3%～6%，但二者与实测数值均非常接近，因此在非达西渗流特征对产能影响较弱时可应用常规产能模型快速评价水平井产能。

2) 对于南海西部不渗透边界影响明显的低渗断块砂岩油藏，考虑不渗透边界对水平井非稳态产能的影响，利用本文建立的水平井非达西渗流模型校正后的计算产能与实测产能十分接近，这表明在采油井与不渗透边界之间部署注水井，在注水受效的情况下可以一定程度抵消不渗透边界对产能的影响。

3) 对于南海西部低渗油藏，从长期生产动态上分析水平井产能阶梯状的变化趋势，具有耗时短、成本低、监测范围广的优势，有助于辅助认识断层的封堵性、砂体间的连通性以及注水的有效性。