基于最长控制链的基因调控网络可控性研究

白雪一,郭炳晖,李佳辉,郑志明

(北京航空航天大学 a.数学、信息与行为教育部重点实验室; b.大数据科学与脑机智能高精尖创新中心,北京 100191)

0 概述

1969年用于研究基因调控网络的随机布尔网络模型被提出[1-2],其利用布尔逻辑和简单的“0”“1”二值构建基因网络的抽象模型,用布尔函数来描述基因之间的促进或抑制关系。1990年,随着“人类基因组计划”的正式启动,系统生物学的时代正式到来,利用布尔网络在分子水平上研究基因和基因调控网络,对于探索生命的遗传秘密、推进人类的疾病诊断和治疗都具有重大的意义。

随机布尔网络能够很好地反映基因网络运行过程中的复杂动态行为[3],特别是基因间的控制关系。基因调控网络的可控性[4]是对基因可能出现的表达形态的一种状态可达属性,布尔网络的可控性是将基因调控网络中基因作用通过布尔函数描述后,根据是否满足Kalman可控性秩条件[5]确定最小驱动节点集,进而确定控制基因的模型化表示。

在布尔网络的可控性方面,目前已经有较多研究成果。例如:文献[6]定义了线性时变控制系统的结构可控性概念;文献[7]将经典的结构可控性理论运用到有向网络的可控性研究中,提出了搜索最小驱动节点集的方法;文献[8]提出了矩阵半张量积方法用于研究布尔网络可控性;文献[9]研究了控制网络的能量需求及能量范围的上下限;文献[10]提出了精确可控性框架;文献[11]研究表明,在一定条件下,无标度网络的实际控制能量服从幂律分布,且与目标状态选择的不确定性有关;文献[12]提出了最长控制链理论。现有对于布尔网络的控制研究,基本是从布尔网络动力学过程角度出发,通过改变节点状态,同时观察动力学传播过程中节点状态的改变对整个网络状态的影响,以及计算网络的鲁棒性等方法进行的。

本文将布尔网络的结构及动力学过程相结合研究布尔网络的控制问题,主要研究对象是一个由6个基因节点构成的实际基因调控网络,其中每个节点的状态由固定的布尔函数决定。由于布尔函数由逻辑表达式构成,当节点的状态取不同值时,网络的控制信号在传递路径上就会有所不同,因此本文分别分析基因网络结构不同时达到结构可控性的最小驱动节点集,并从控制能量最少的角度研究其最长控制链(Longest Control Chain,LCC)。

1 布尔网络

本文研究的基因网络包含6个节点:CyclinD1(节点1),CyclinE(节点2),E2F1(节点3),Myc(节点4),p27Kip1(节点5),RB(节点6)[13]。

CyclinD1是一个由人类CCND1基因所编码的蛋白质,其基因属于高度保守的细胞周期家族,该家族在整个细胞周期中蛋白丰度具有周期性变化的特点;CyclinE节点表示活性细胞周期蛋白复合物;E2F1是细胞内重要的转录因子,对细胞的增殖、分化和凋亡都发挥着关键性的作用;Myc基因家族及其产物可促进细胞增殖,在多种肿瘤形成过程中处于重要地位;p27Kipl蛋白为细胞周期素依赖性蛋白激酶抑制因子(CDKI),在调控细胞周期中具有十分重要的作用;RB是一种肿瘤抑制基因,是最早发现的抑癌基因。

在文献[13]研究中,这6个基因之间的相互关系是已知的。在没有活性细胞周期蛋白CyclinD1的情况下,Myc和E2F1都会促进CyclinD1的生成。相反地,当细胞周期蛋白CyclinD1已经存在时,Myc或者E2F1都可以维持高于阈值的细胞周期蛋白Cyclin D1的量。当不存在RB(阻断其转录)和p27Kip1(阻断其活性)且E2F1转录时,CyclinE处于激活状态。在没有RB的情况下,活化的E2F1或Myc可以诱导E2F1转录。当RB存在时,E2F1无效。E2F1能激活Myc转录。CyclinD1或CyclinE可抑制p27Kip1的活性。RB在没有细胞周期蛋白Cyclin D1,并且当存在活性p27Kip1或没有活性细胞周期蛋白复合物CyclinE的情况下是活跃的。基于此,该基因网络各节点的布尔函数如表1所示。

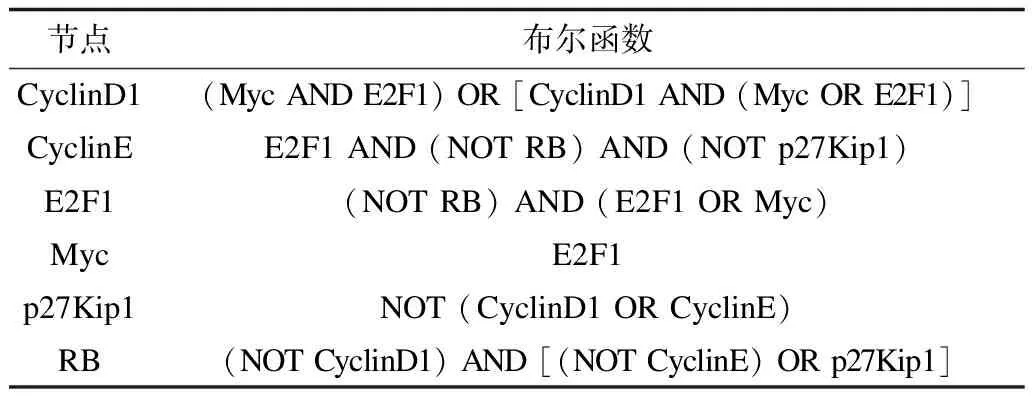
表1 各节点的布尔函数

本文做的所有实验都是基于上述网络进行的,基因网络及其基本结构如图1所示。

2 相关算法

2.1 结构变化

网络的结构一般是不会发生变化的,本文讨论的网络结构变化是在网络信息传递的角度下进行的,如果信息无法从一个节点沿着边传递到另一个节点,则认为这条边在这种情况下无法传递信息,在整个网络中,无法传递信息的边可以视为不存在的。

边无法传递信息,一般是由于布尔函数是一个渠化函数[14],即一个节点的布尔函数的取值完全由一个邻居节点的状态决定,其他邻居节点的状态对布尔函数的取值完全没有影响。在这种情况下,没有影响的邻居节点与该节点之间的边无法传递邻居节点对该节点的影响。

假设布尔网络中存在如图1(b)所示的结构,且节点0的布尔函数为f(x1,x2)=x1ANDx2,则节点0的真值表如表2所示。

表2 节点0真值表

由表2可见:当x1、x2的取值中存在0时,f(x1,x2)的取值为0;当x1取值为0时,无论x2的取值是多少,f(x1,x2)的取值都为0,即此时x2的取值无法影响到f(x1,x2)的取值。从能量传递的角度分析,节点2上所携带的能量无法传到节点0上,在能量传递上,节点0和节点2之间的边相当于不存在。同理,当节点2的取值为0时,节点1与节点0之间的连边从能量传递的角度而言是不存在的。

基于上述规则,在某些网络状态下布尔网络的某些边可以忽略不计,因此,布尔网络的结构就发生了变化。

2.2 最大匹配算法

根据控制理论,如果一个系统在适当的输入条件下,能够在有限时间内从任意初始状态到达任何期望的最终状态,则这个系统是可控的。这个定义与直观的控制概念相一致,即通过适当地操纵几个输入变量将系统的状态引导到所需状态,例如驾驶员通过操纵踏板和方向盘引导汽车以期望的速度向期望的方向移动。

文献[7]将经典的控制理论运用到解决复杂网络可控性的问题上,建立复杂网络的结构可控性分析框架,提出一种搜索使网络满足Kalman可控性秩条件的最小驱动节点集的方法,从理论上证明了网络的最大匹配决定了控制整个网络所需的最少控制节点,解决了大型复杂网络的结构可控性问题。

在图论中,一个匹配是网络的一个边的集合,其中任意2条边都不相邻,即没有公共节点,最大匹配即网络中包含边数最多的匹配[15]。给定一个有向网络,为了找到其最大匹配,需要先将其转换为二分网络,即将网络中的节点分为2个互不相交的子集,网络中所有的边都可以由一条二分网络中左边节点指向右边节点的边表示,同一边的节点中不存在连边。二分网络中找最大匹配的经典算法是匈牙利算法[15],其核心就是寻找增广路径,通过增广路径来求二分网络的最大匹配。匈牙利算法的具体流程如图2所示。

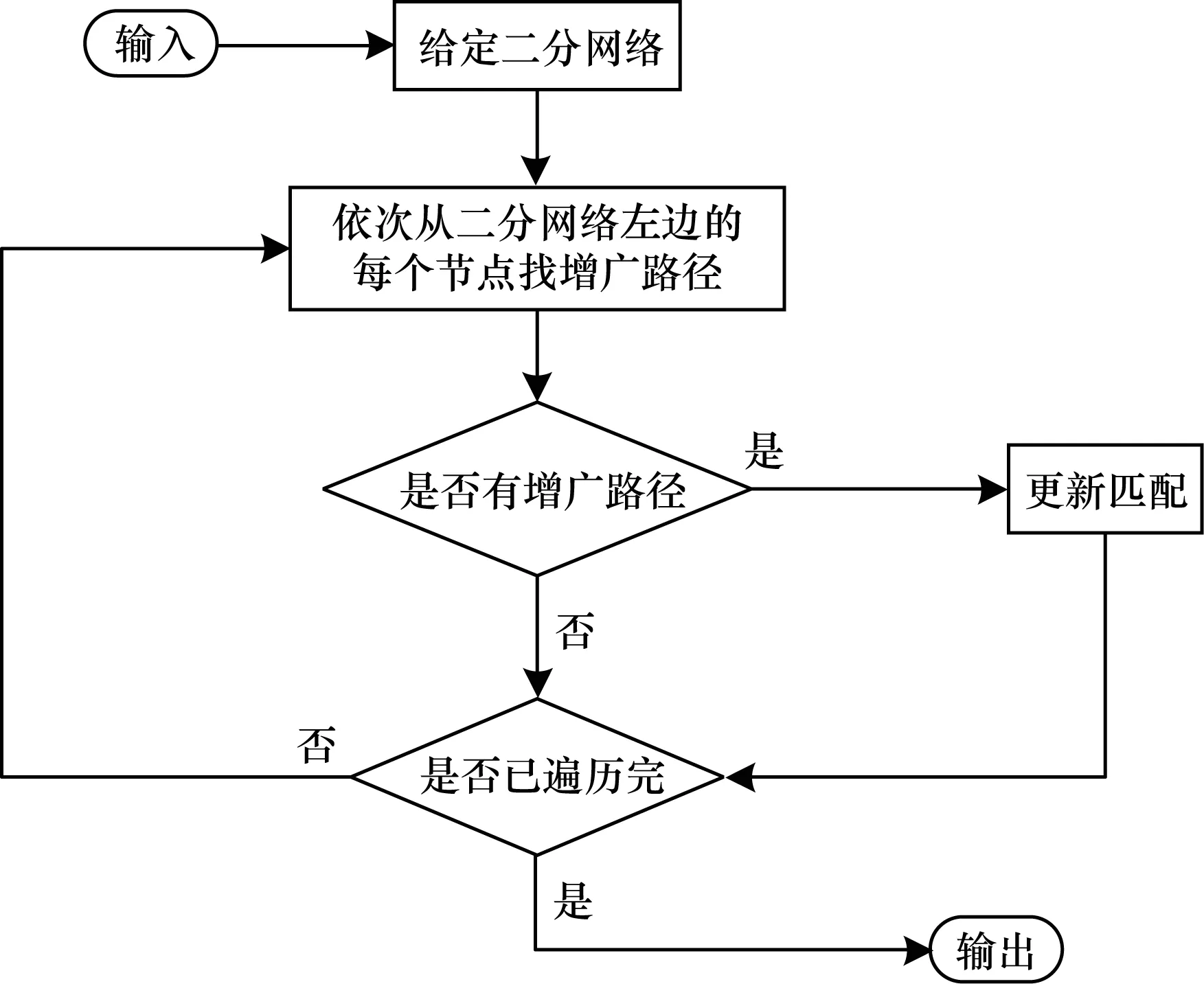
图2 匈牙利算法流程

定义最大匹配中边指向的节点为匹配节点,网络中除了匹配节点外都是非匹配节点,而非匹配节点就是复杂网络通过最大匹配算法找到的最小驱动节点集。

图3为网络状态为[0,0,0,0,0,0]时基因网络的二分图,以及最大匹配算法找到的驱动节点集,其中虚线框节点为驱动节点,虚线的边为最大匹配。

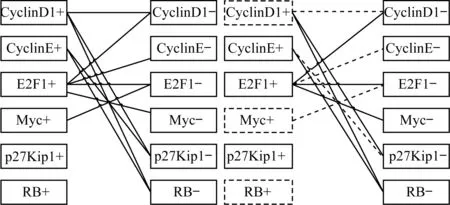
图3 基因网络的二分图

2.3 最长控制链

最小驱动节点集旨在用最少的输入信号控制整个网络,但从能量角度而言,输入信号数量最少并不一定代表着控制网络所需的能量是收敛的。文献[12]提出了一种基于网络结构特性解释网络中标度行为的理论,即最长控制链,并从理论上证明网络的最长控制链的长度与控制整个网络所需的能量处于同一数量级,基于此,给出一种切实减少网络控制能量的方法。

在网络中,控制能量是从外部信号通过驱动节点传递到非驱动节点的,因此,需要先对网络进行最大匹配算法,找到网络的n个驱动节点。根据最大匹配算法,可以将网络分为n个分支,每个分支为一个驱动节点开始的一维链条,可以认为控制信号就是沿着分支进行传递的。但是在能量传递方面,由于节点之间的耦合,一个节点的状态变化会影响到其所有邻居节点,因此,能量并不只沿着分支传播,分支之间也可以传播。基于此,任意非驱动节点都可以由所有与其之间有路径的驱动节点的能量控制,由驱动节点开始、由非驱动节点结束的链条称为控制链。

直观上,控制节点所需的能量随着节点的增加呈指数级增长,因此,要控制一个非驱动节点所需最少的能量,可以由其最短控制链决定。而控制整个网络的能量,即控制网络中所有节点的能量,由控制所有非驱动节点所需的最大能量决定,即所有非驱动节点的最短控制链中的最长者决定,这就是网络的最长控制链。网络最长控制链搜索算法如下:

算法最长控制链搜索算法

输入网络G,驱动节点集,驱动节点数n,非驱动节点集,非驱动节点数m

输出最长控制链

for i=1:m

for j=1:n

计算非驱动节点i与驱动节点j之间的最短路径

将该最短路径存入变量DL中

End

将变量DL中长度最短的路径存入变量NDL中

End

输出NDL中长度最长的路径,即为最长控制链

通过上述算法得到基因网络在网络状态为[0,0,0,0,0,0]时的最长控制链,如图4所示。其中,最上排3个基因为驱动节点,虚线边即为最长控制链,灰色基因为最长控制链终点。

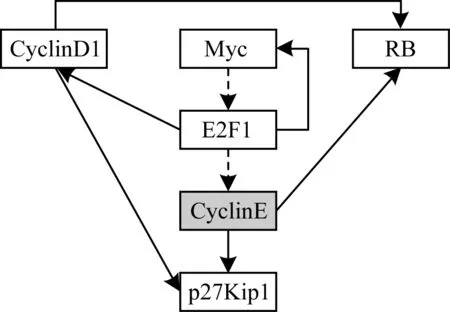
图4 基因网络在网络状态为[0,0,0,0,0,0]时的最长控制链

3 实验与结果分析

本文对上述基因网络所有可能的状态都进行实验,即对每一种网络状态,根据节点的布尔函数重构其网络结构,由最大匹配算法发现驱动节点集,找到最长控制链。其中节点被选为驱动节点的频次分布如图5所示。从中可以看出:节点2、节点3、节点5被选为驱动节点的次数较少,即在进行网络的最大匹配时,指向这3个节点的边在较多最大匹配中存在;节点1、节点4、节点6被选为驱动节点的次数较多,其中节点6次数最多,节点1和节点4次数持平,稍少一些,但频次仍远超其他节点。

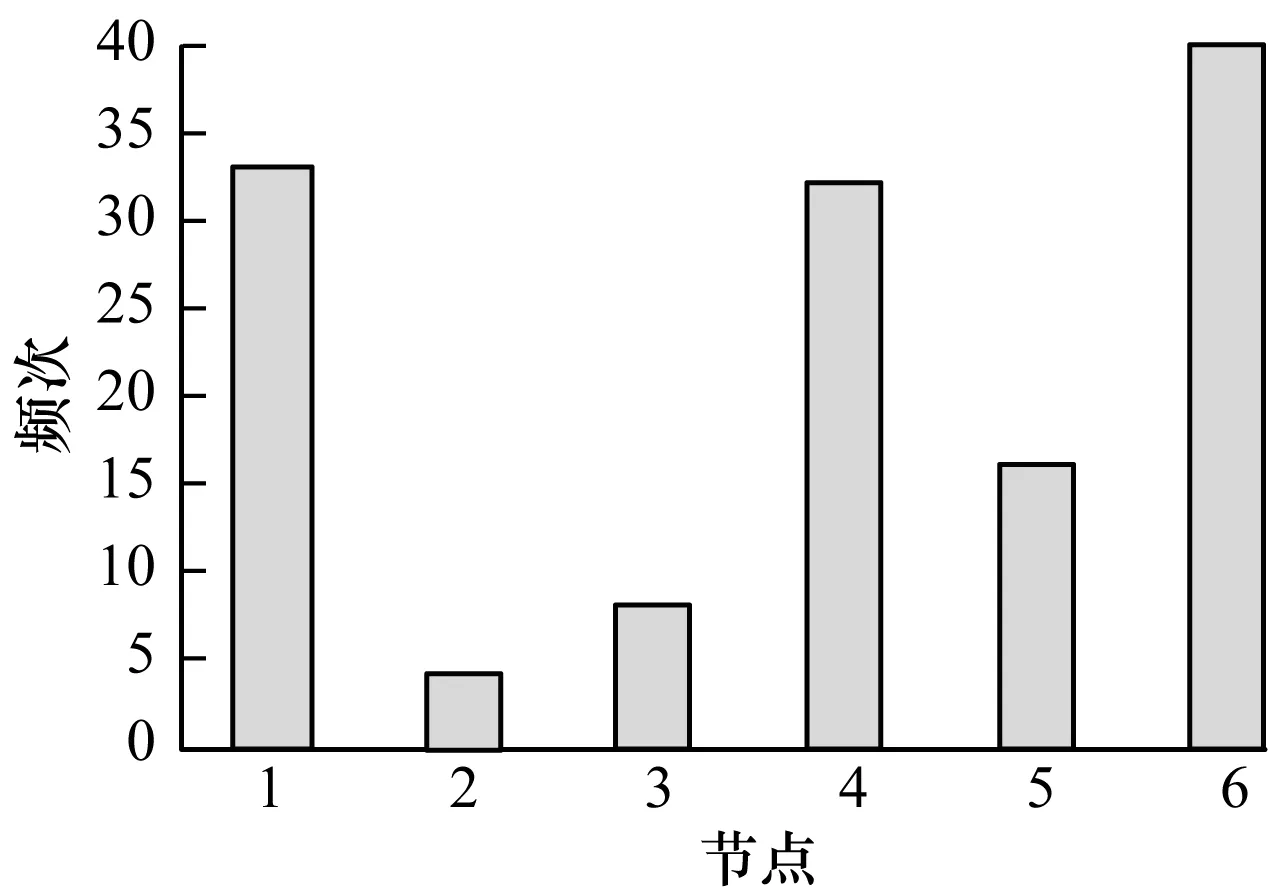
图5 所有网络状态下节点被选为驱动节点的频次分布

各节点取值为0和1时,节点被选为驱动节点的频次比较如图6所示。从中可以看出:当节点1取0时,节点1和节点4有更大的概率被选为驱动节点,节点2、节点5没有被选为驱动节点过;而当节点1取1时,节点6以较大的概率被选为驱动节点;当节点3的状态取0时,节点3和5没有被选为驱动节点过,节点4被选为驱动节点的次数最多;而当节点3状态取1时,节点2和4没有被选为驱动节点过,节点1、节点5、节点6被选为驱动节点的次数最多且相差不大;每个节点被选为驱动节点的情况在节点2、节点4、节点5、节点6的状态取0或1时差别不大,只有个别节点稍有差别。

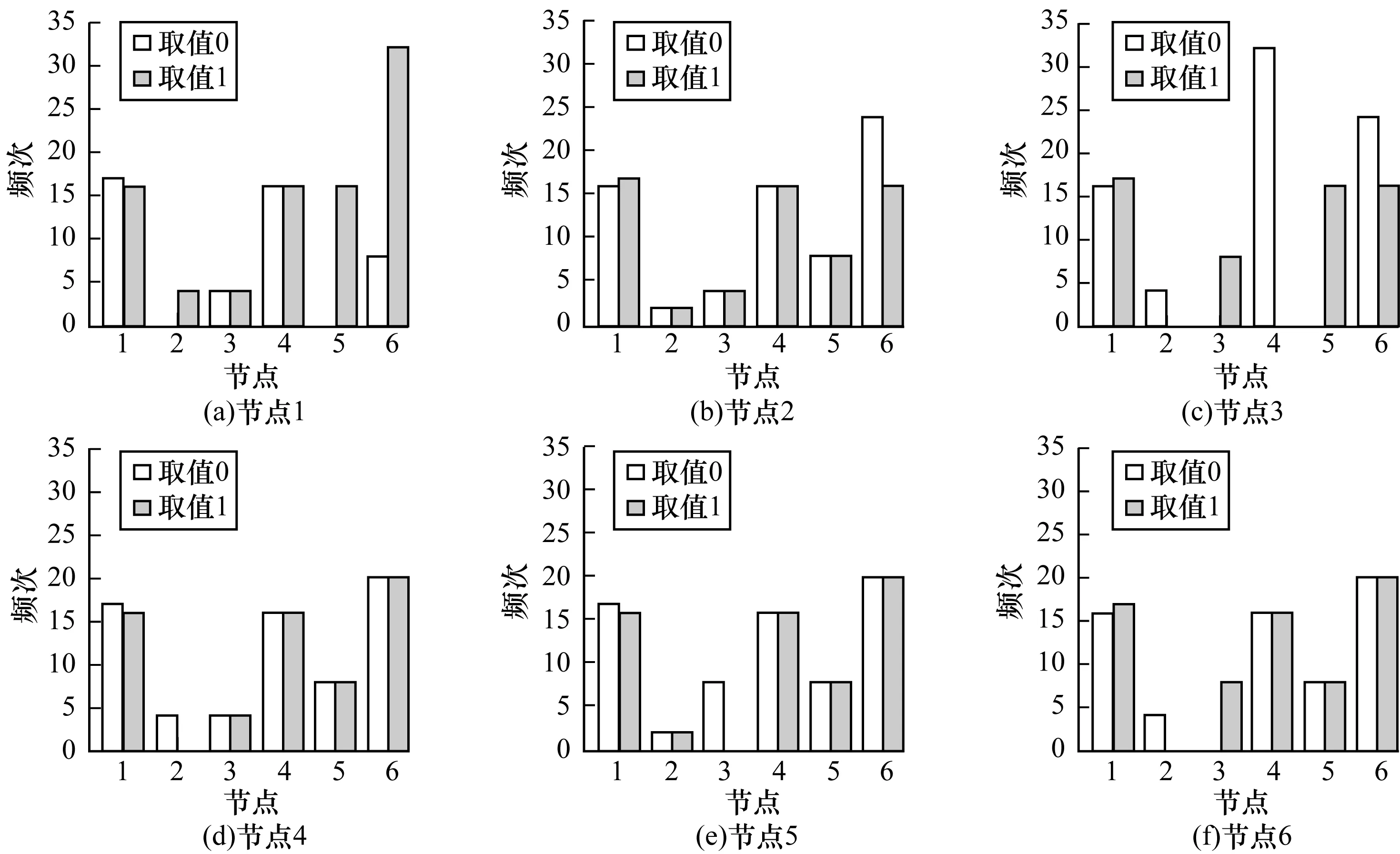
图6 各节点在不同状态取值时被选为驱动节点的频次分布

通过比较可以发现,节点1、节点4和节点6被选为驱动节点的次数在任何情况下都是最高的,这与图5结果是一致的。因此,从结构可控性的角度出发,可以认为节点1、节点4、节点6更适合作为控制信号输入的节点。结合实际基于网络,在多数状态下,控制基因CyclinD1、Myc、RB,基本可以保证网络的结构可控性。

所有网络状态下LCC长度及各节点成为终点的频数分布如图7所示,其中,None表示网络中不存在驱动节点,即网络本身为结构可控,inf表示驱动节点与非驱动节点间无路径可以到达,距离为无穷大。

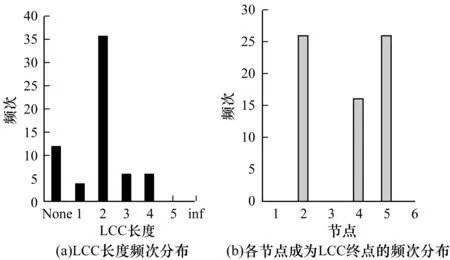
图7 LLC长度及各节点成为终点的频次分布

由图7(a)可以看出,最长控制链的长度为2的情况占大部分。因此,在多数情况下,控制基因网络的能量与控制由3个节点组成的链式网络的能量为同一数量级。通过分析可知,最长控制链的终点是网络中最难控制的节点,由最长控制链理论可知控制网络的能量实际为控制LCC终点的能量。图7(b)所示为各个节点成为最长控制链终点频次分布,从中可以看出,节点1、节点3和节点6在任何情况下都不是LCC终点,而节点2和节点5为LCC终点的次数明显超过节点4。在基因网络中,基因CyclinE和p27Kip1更难控制。

图8所示为各节点在不同状态取值时最长控制链长度的频次统计。从中可以看出:在节点1状态为0时,最长控制链长度为2的频次不是最高的;在节点3状态为1时,最长控制链长度为2和为None的频次几乎相等;在其余情况下,长度为2的最长控制链频次都是最高的。节点1状态为1时,最长控制链的长度只有2种可能,即1和2;节点3状态为0时,最长控制链的长度为2、3、4,即基因E2F1处于抑制状态时,控制网络所需的能量要高于普通情况。

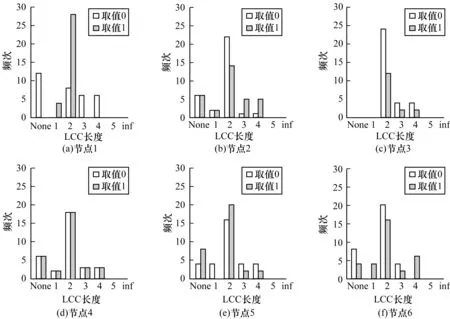
图8 各节点在不同状态取值时的LLC长度频次分布

通过比较可以发现,网络最长控制链的长度在各节点状态改变时变化不是很大,基本长度为2的最长控制链的次数远超其他长度出现的次数,由此可以推断网络最长控制链的长度即控制网络所需的能量与网络的状态关系不是很大,主要由网络的结构控制。

由于网络状态的不同,能量传输角度上网络结构会发生变化,笔者对所有可能的网络状态的网络结构进行研究发现,网络的最长控制链的长度可能和网络的平均聚类系数、强连通分支数、平均连通性有关。图9和图10分别展现了最长控制链长度与网络结构的关系以及各节点特征向量中心性。其中,ac表示网络的平均聚类系数,nscc表示网络的强连通分支数,anc表示网络的平均连通性。可以看出,随着最长控制链长度的增加,网络的平均聚类系数增加,平均连通性增加,强连通分支数下降。

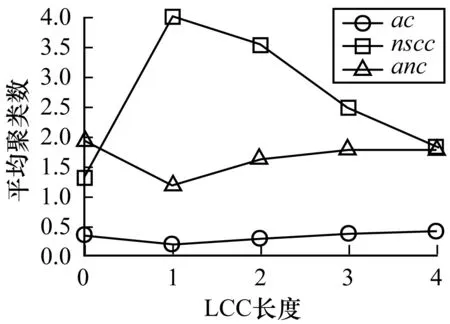
图9 LLC长度与网络结构的关系

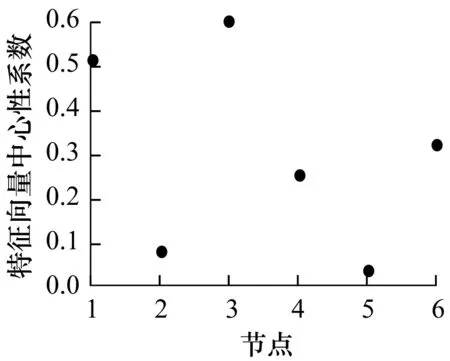
图10 各节点特征向量中心性

各节点在不同状态取值时成为最长控制链终点的频次分布如图11所示。

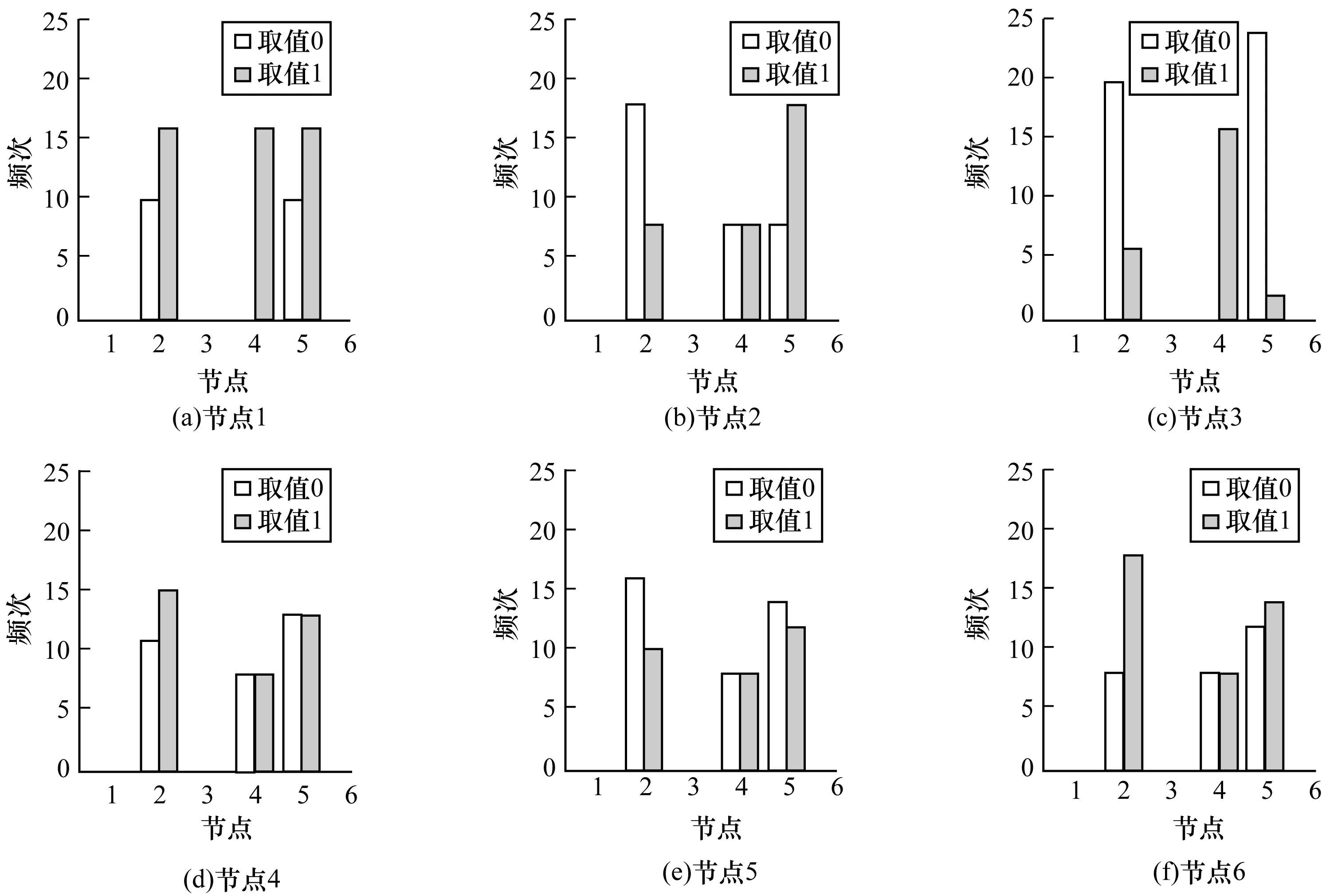
图11 各节点在不同状态取值时成为LLC终点的频次分布

从图11可以看出,每个图中都是只有节点2、节点4和节点5的数据,而节点2和节点5的频次普遍高于节点4的频次,但节点3的状态为1时,节点4为LCC终点的频次高于节点2和节点5,即当基因E2F1处于激活状态时,基因Myc决定者控制网络的能量。

结合驱动节点的统计情况可以发现,节点3以小概率被选为驱动节点,且不会成为最长控制链的终点,即节点3到驱动节点的最小距离基本上为1。根据网络结构,对比节点3和节点2、节点5,可以发现:在被高概率驱动节点1、节点4、节点6指向方面,节点3被节点4和节点6指向,而节点2和节点5分别被节点6和节点1指向;节点4既能以较高的概率被选为驱动节点,又能以一定的概率作为最长控制链的终点。实验数据表明,除了网络自身结构可控的情况之外,节点4或者是网络的驱动节点,或者是网络最长控制链的终点,这可能是由于节点4只被节点3指向,而节点2和节点5以高概率作为网络最长控制链的终点,小概率被选为驱动节点,可能与节点的特性有关系。对所有网络进行研究后发现,这可能与节点的特征向量中心性有关,如图10所示,节点2和节点5的特征向量中心性均低于其他节点。

4 结束语

本文针对人类细胞周期中的基因调控网络,基于节点的布尔函数,根据网络状态对基因网络的结构进行重构,并利用最大匹配算法和最长控制链理论,从结构可控性和控制能量的角度对其进行分析。分析结果表明:在多数状态下,控制基因CyclinD1、Myc、RB可以保证网络的结构可控性;控制基因网络的能量与控制由3个节点组成的链式网络的能量为同一数量级;基因CyclinE和p27Kip1较难控制;网络的最长控制链的长度可能与网络的平均聚类系数、强连通分支数、平均连通性有关;当基因E2F1处于激活状态时,基因Myc决定者控制网络的能量;节点作为最长控制链的终点的概率可能与节点的特征向量中心性有关。

由于本文研究的基因网络只有6个节点,网络规模较小,代表性较弱,网络最长控制链的长度及终点与网络结构的具体关系并没有明确找出,因此后续将对各种类型的网络进行研究,从理论上探索网络的能量传输路径与网络结构的关系。