基于网络拓扑与节点元数据的社团检测算法
刘宇廷,毕海滨,郭 强,倪颖杰
(江南计算技术研究所,江苏 无锡 214000)
0 概述
不同领域多样化的系统可以表示为复杂网络,例如科技系统、生物系统和社会系统[1]。针对复杂网络研究的一个热门方向是社团检测,社团结构在复杂网络中普遍存在[2]。通过挖掘网络中的社团,可以帮助理解网络拓扑结构特点,揭示复杂系统内在功能特性,理解社团内个体关系及行为的演化趋势[3]。
传统社团检测方法基于网络拓扑结构的统计特性建模进行分析与挖掘,研究人员通常假设得到的社团能够表示具有相似特性或功能的节点集合。当前,一些研究已经证实了这个假设下得到的社团与网络中元数据代表的团组是有区别的[4]。所以,许多研究人员期望能够结合其他信息进行社团检测,以发现网络中的真实社团结构。
在真实复杂网络中,网络除了拓扑信息之外,还有节点上的元数据与边上的元数据。例如,社交网络[5]如新浪微博包含用户的个人信息(姓名、年龄、爱好等),引用网络包括用户的姓名、关键词和文章的摘要信息、邮件网络中发送邮件的内容等。通常属于一个社团中的节点一定共享了某些相似的属性,反之可以认为节点的属性影响了社团的结构,结合这些元数据将会提高社团检测的准确性。近年来,研究者提出许多社团检测算法,以期能够通过元数据提高社团检测的准确程度。文献[6]利用2个节点之间共同好友的个数衡量节点之间的相似度,但是这个方法需要遍历整个网络,复杂度高;文献[7]利用谱聚类算法找到初始划分,利用节点的度、内度、外度建立条件概率表,选择一部分最有可能的点作为根节点,构建贝叶斯网络来找到最优社团结构;文献[8]通过定义节点与节点、节点与社团之间的互动力作为社团检测的指标;文献[9]提出一种基于自然最近邻居概念的社团检测算法CD3N算法,以结构相似度为基准,构造网络中节点的自然邻居从而发现社团结构;文献[10]指出当前很多方法只是基于网络中边的连接信息而忽视了节点上的信息,将边与节点信息同时存在的网络建模为NSBM,并研究基于似然推理的算法;文献[11]提出通过改进基准网络建模,将节点上的元数据(metadata)社团编号融合到模型中,以自动判断这种元数据能否帮助网络划分,使得到的网络划分评价分数更高。但是算法中使用的元数据是社团归属标签与年龄、性别等单一属性,在刻画节点特征上并不完整,例如社交网络中一个节点的描述通常是一段文字、图片等信息。
针对文献[11]算法存在的问题,本文提出基于网络拓扑与节点元数据的社团检测算法CDNTNM。首先假设网络中节点具有混合高斯分布,构建节点元数据复杂分布的基准网络;然后建立融合网络结构与节点元数据的网络模型,研究混合高斯模型与基准网络模型的融合方法;最后分析真实网络数据样本分布,提出特征选择方法。
1 基于随机块模型的网络建模
1.1 随机块模型
随机块模型[12]通常建模为包含社团结构的网络,用于辅助社团发现。随机块模型通常假设网络中社团数量是固定的,网络中的节点一定归属于其中某个社团,处于不同社团中的节点以概率prs建立连边。调整同一个社团内节点之间边连接的概率,可以生成符合社团结构定义的网络结构,即社团内部连边密集而社团之间连边稀疏,随机块模型的似然函数为:
(1)
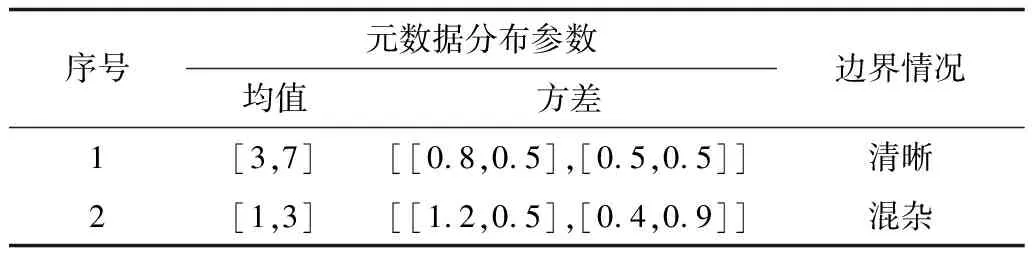
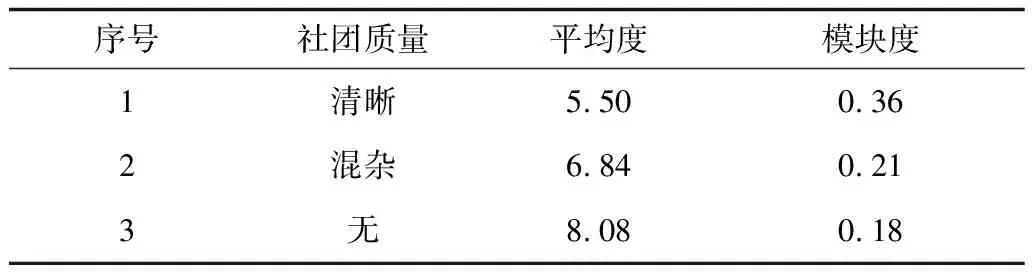
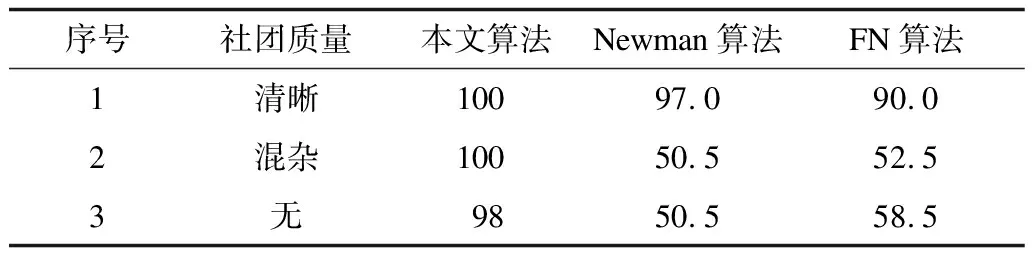
其中,Aij代表网络的邻接矩阵中第i行第j列的元素,取值为1表示节点i和节点j之间存在连边,取值为0表示不存在连边,si表示节点i所属的社团编号,i 真实复杂网络具有“无标度”特性[14],而随机块模型不满足这个特征,所以,在拟合现实世界网络数据时效果很差。文献[15]通过在块模型中添加度数相关的变量,使得节点之间边的概率prs能够与节点度数匹配(如节点具有边的总量),从而满足“无标度”这个特性。改进后的模型中定义节点之间边的概率为: puv=dudvθsu,sv (2) 其中,du为节点u的度数,θst是指定的参数,θsu,sv能够让模型适合任意度数序列,即度数分布。 真实复杂网络中节点上的元数据通常呈现信息多、形式杂的特点,例如:一个校园社交网络中学生具有性别、年龄、种族等信息;一个食品网络顾客信息包含体重、爱好等信息。节点上的信息不仅具有标量信息和连续变量信息,甚至还有文本信息,无疑对社团分布影响非常大。通常具有相似信息的节点元数据构成的特征符合一定的分布,比如高斯分布。所以,在本文的实验中,将这类具有多维度特征的向量建模为多维高斯模型。为方便观察,实验中使用二维高斯分布数据作为节点元数据,数据来自2个具有相同方差、不同均值的高斯分布,参数如表1所示,通过参数可以将2个分布的边界控制为清晰与混杂。 表1 节点元数据分布参数设置 (3) 由随机块模型可知基于网络拓扑结构的先验概率模型为: (4) 基于这两个模型生成网络的似然概率为: (5) 其中,A为网络的邻接矩阵,Γ为参数γsx的矩阵,Θ为参数θst的矩阵。针对复杂网络节点具有高维元数据的情况,可以定义:对于所有节点元数据X={x1,x2,…,xn},假设每个节点u分配到社团s的概率基于节点u的元数据xu,xu∈n,n≥1,定义概率为γsx,使用高斯混合模型对社团归属建模。高斯混合模型的概率模型为: (6) 对于每个节点的元数据xi,其由第k个高斯模型生成的概率为: (7) 其中,N(xi|μk,δk)为xi属于分布k的后验概率,如式(8)所示。 (8) 因此,基准网络中每个节点社团分配的先验概率模型为: (9) 最终得到基于这两个模型生成网络的似然概率为: P(A|Θ,π,μ,σ,x)= (10) 在上述式中,π为高斯混合模型的权值向量,μ、δ为高斯混合模型的均值矩阵与方差矩阵。通常可以使用EM算法求解式(9),通过估计模型中的参数,得到模型的最优解,从而得到社团分布。 设有函数f(x),x∈,如果∀x有f″(x)≥0成立,则f(x)是凸函数。如果x是一个向量,而且其hessian矩阵H是半正定的(H≥0),那么f(x)是凸函数。如果f″(x)>0或者H>0,那么称f(x)是严格凸函数。 Jensen不等式表述为:如果f是凸函数,X是随机变量,那么E[f(x)]≥f(EX),特别地,如果f是严格凸函数,那么E[f(x)]=f(EX),当且仅当p(x=E[X])=1,即X是常量。这里f(EX)是f(E[X])的简写[15],其几何表示如图1所示。 图1 Jensen不等式的几何表示 给定的训练样本是X={x1,x2,…,xn},样本之间相互独立,对于每个样本xi,存在隐含类别z使得p(x,z)最大。p(x,z)的最大似然估计公式如下: (11) 求解第1步是对极大似然取对数,第2步是对每个样例的每个可能类别z求联合分布概率和。但是直接求θ一般比较困难,因为有隐藏变量z存在,所以如果能够确定z,则求解便可以化简。 EM是一种解决存在隐含变量优化问题的有效方法。由于不能直接最大化(θ),因此不断地建立(θ)的下界(E步),然后优化下界(M步)。可以简单描述为:对于每一个样本xi,用Qi表示该样本隐含变量z的某种分布,且Qi满足的条件是例如:要将动物分类,如果隐藏变量是体重,那么就是连续的高斯分布;如果按照隐藏变量是食肉或食草,那么就是伯努利分布。 由此可以得到以下公式: (12) (13) (14) (15) p(z(i)|x(i);θ) (16) 由上述推导可以发现,固定θ后,Qi(z(i))的计算公式就是后验概率,解决了Qi(z(i))如何选择的问题。这一步就是E步,建立(θ)的下界。接下来的M步,就是在给定Qi(z(i))后,调整θ,去极大化(θ)的下界(在固定Qi(z(i))后,下界还可以调整的更大)。(θ)是单调增加的,所以,算法在(θ)趋于不变时收敛。 将2.2节的推导应用到式(10)中,可以得到: logaP(A|Θ,π,μ,σ,x)= (17) (18) 由式(18)可以看出,Qi(z(i))为后验概率分布,表达式为: (19) 对式(18)应用EM算法,可以得到CDMTMN算法对应的最优解,算法求解过程与EM算法中对应步骤描述如下: 1)CDNTMN算法初始化,输入数据集G,检测网络G中的社团结构,得到模型似然概率值并输出网络节点社团归属分布Q。初始化Θ、μ、δ、π的值。 2)E步,固定参数Θ、μ、δ、π的值,使用它们计算社团后验概率分布Q。 3)M步,固定Q,更新参数Θ、μ、δ、π的值。 4)计算似然值与评价函数,查看是否收敛。如果否,从第2个步骤开始执行。 5)算法收敛,算法结束,得到模型似然概率值与社团最优分布Q。 仿真硬件平台为:E4310,8 GB,Win7 x64,对比算法选用Newman的算法[11]、FN算法[17]。 3.1.1 基准网络生成 在电脑生成的基准网络上测试算法性能,基准网络基于Newman改进后的随机块模型生成。基准网络的参数包括:网络中社团数量K(定义K=2);网络节点数量N;社团内部与社团之间边连接概率的混合参数Γ,为K×K矩阵;网络中节点元数据维度D;节点元数据边界清晰参数C。 通过设置不同的参数,生成用来对比的基准网络,实验中使用的参数如表2所示。 表2 基准网络参数 具有相同的节点规模N、节点上的元数据维度D与社团内边连接概率pin,不同基准网络通过社团间边连接概率区分,为表征各个基准网络的社团结构程度,通过调整社团间边的连接概率,将基准网络分为3个等级:清晰,混杂,无,分别对应具有明显的社团结构、社团边界较明显、无社团结构(达到Newman所说的临界值)。基准网络节点数量N=200,元数据维度D=2,社团内边连接概率pin=0.1,生成的网络指标详见表3。 表3 基准网络 3.1.2 基准网络实验结果 由于EM算法求解参数最优值时,存在局部极值,因此在本实验中基于算法多次运行,得到算法平均性能,衡量标准使用准确率和NMI。NMI是用来衡量社团检测与“真实”情况的方法[18],NMI的值域在0到1之间,如果节点元数据能够非常准确地预测社团成员,则达到极大值。 1)设置不同网络参数,本文算法性能对比如图2所示。 图2 N=200时各参数下的算法性能 2)本文算法与Newman算法和FN算法的正确率对比如表4所示。 表4 各算法在不同社团质量下的正确率对比 % 为体现算法在真实网络上的表现,选择具有真实社团信息并且广泛使用的Facebook数据集作为算法的验证网络。 Facebook数据集来自斯坦福大学(http://snap.stanford.edu/data/),其中包含10个用户网络(ego-network),共包含193个朋友圈和4 038位用户。由于实验需要真实社团信息,所以,选择其中具有人工标注的用户网络。每个网络包含一位处于中心的用户,由用户标注社团成员(即朋友圈成员),社团数量平均8个,包含不属于任何社团的用户 3.2.1 Facebook网络预处理 通过预处理,提取其中两位用户的用户网络A和用户网络B,其网络关系如图3所示,可以看到用户A的网络社团结构明显,用户B的网络社团结构不明显。 图3 用户网络真实社团划分结果 3.2.2 特征提取 出于对用户信息安全的考虑,数据集中的用户特征被映射为对应的值,形成了一个特征矩阵,本文对其做一次主成分分析,并约减到合适的维度。通过实验发现,用户网络A维度为133维、用户网络B维度为40时,可以保留原数据的90%的信息。用户网络相关参数如表5所示。由模块度可以看出网络A比网络B的社团结构明显。 表5 用户网络参数 3.2.3 真实网络实验结果 通常使用BIC准则评价高斯混合模型, 图4中可以看到,用户网络A社团数N=7和用户网络B社团数N=6时,bic值达到最小。 图4 用户网络社团划分的bic值对比 与FN算法得到的社团划分对比,准确率与NMI对比如表6所示,由于传统社团检测算法FN无法比较NMI,因此只能对比社团检测的准确率。 表6 用户网络各算法性能对比 % 3.3.1 基准网络实验结果分析 由图3可以看出,当元数据边界明显时,CDNTMN算法性能基本不会受到拓扑结构的影响,准确率稳定在90%以上,随着社团质量下降,出现了少量的无法收敛的情况。当元数据边界不明显时,算法性能随着社团质量下降而迅速下降,当社团之间边连接概率大于等于0.06时,算法多次运行的结果中,多次出现无法收敛的情况,同时,社团准确率非常不稳定。 由表4可以看出,本文算法能够结合节点元数据与拓扑结构检测社团结构,在复杂网络中社团结构不明显时,基于网络拓扑结构的算法正确率仅有52.5%,而本文算法可以稳定在90%以上。但是当节点元数据分布边界不明显,同时社团之间边连接概率达到Newman定义的条件时,算法性能也会急剧下降。 3.3.2 Facebook网络实验结果分析 在Facebook用户网络上的实验可以发现,用户网络A的模块度在0.3左右,节点元数据与社团结构相关程度高,实验结果较好。用户网络B社团结构不明显,同时节点元数据所标注的社团与算法发现的社团之间存在差异,影响因素是人工采集的特征不完整。 本文算法检测到的社团与真实社团对比具有如下特点: 1)如果现实世界网络中社团结构明显,则任何算法都能够准确地发现社团结构。 2)如果现实世界网络中社团结构并不明显且元数据不能够反映社团划分,如用户网络B,则本文算法准确率较传统社团检测算法有较大的提升。 实验中发现用户特征维度各不相同,且用户特征矩阵为稀疏矩阵,这在一定程度上给用户特征建模造成一定的困扰。如何确定一个用户的主要特征,例如,文献[19]发现虽然在Facebook网络中。用户来自世界各个地方的大学,但是一个用户的朋友网络中,不同大学数量却不多,所以,这种具有强烈社团归属特性的特征在实验中没有重点利用。 本文结合社团检测算法的现有研究,提出一种基于网络拓扑结构与节点元数据的社团检测算法。相比传统社团检测算法,该算法在基准网络中的正确率有显著提高,结合网络节点元数据,即使在网络中社团结构不明显的情况下,也可以生成较为准确的估计;由于真实网络的节点元数据维度较高,因此其使用主成分分析约减特征维度,降低了计算复杂度,但是这种特征提取方法仍然比较粗糙,最后的社团检测结果与人工标注社团有一定相似,不可避免地存在误差。 本文算法使用的基准网络具有固定的社团数量且没有考虑网络元数据重叠的情况。此外,真实网络中节点元数据是脱敏映射后的稀疏矩阵,与真正的元数据还具有差距。下一步将针对上述情况做深入研究。1.2 随机块模型的改进
2 基于网络拓扑与节点元数据的社团检测
2.1 基准网络似然概率模型建模

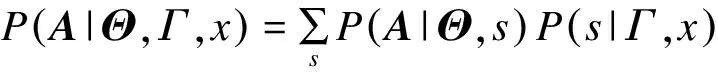

2.2 基于EM算法的推导




2.3 融合混合高斯模型的似然概率模型求解
3 实验与结果分析
3.1 基准网络


3.2 真实网络




3.3 结果分析
4 结束语

