无线传感器网络立体定位算法与仿真

张留朝，张 彭，刘贞德

（潍坊学院 计算机工程学院，山东 潍坊 261061）

0 引 言

在无线传感器网络中，位置信息对传感器网络的监测活动至关重要，事件发生的位置或获取信息的节点位置是传感器节点监测信息中的重要组成部分，没有位置信息的监测消息是无意义的[1]。因此，无线传感器网络节点定位是其最基本的功能之一，对无线传感器网络应用的有效性起关键作用。

无线传感器定位算法包括基于测距的定位和无需测距的定位两种[2-3]。基于测距的定位算法是利用接收信号强度指示（RSSI）估计待定位节点到参考节点的距离，然后根据测距定位算法计算待定位节点的坐标。典型的测距定位算法包括多边定位、边界盒定位、MDS-MAP等[4]。无需测距的定位利用网络连通性、节点分布、跳数等方法实现定位，典型的无需测距的定位算法包括质心定位、DV-HOP定位和APIT定位等[5-6]。

上述定位算法中，无论是基于测距的定位，还是无需测距的定位都存在以下两方面的局限：

（1）信标节点的位置无法移动；

（2）待定位节点和信标节点[6]必须在同一平面上，否则定位精度会受影响。

针对上述局限，本文提出了无线传感器网络的立体定位方法。

1 立体定位算法描述

本文提出了一种无线传感器网络的立体定位算法，设立多个信标节点和一个终端用户节点，所设立的信标节点不在同一平面上，而是位于“棱锥”或“棱柱”的顶点。建立三维直角坐标系，标定信标节点在直角坐标系中的位置坐标。信标节点在三维直角坐标系中的相对位置和坐标始终不变（信标节点发生移动时，直角坐标系随参考节点的移动而移动，这样信标节点在直角坐标系中的位置坐标即可保持）。信标节点负责接收待定位节点发射的无线信号，并根据RSSI测距公式计算出待定位节点到该信标节点的距离。然后把计算得到的这一距离和该待定位节点的身份标识发送至终端用户节点。终端用户节点根据接收到的信息计算出待定位节点的位置坐标。

1.1 信标节点分布模型

本文提出的无线传感器网络立体定位算法的信标节点不在同一平面上，分别位于“棱锥”或“棱柱”的顶点。建立三种信标节点分布模型，即“三棱锥”分布模型、“三棱柱”分布模型和“四棱柱”分布模型，分别如图1～图3所示。

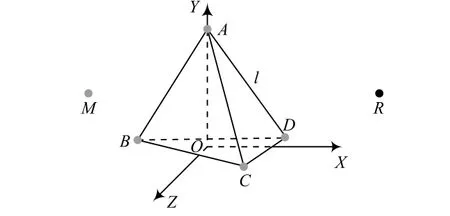
图1 信标节点“三棱锥”分布模型

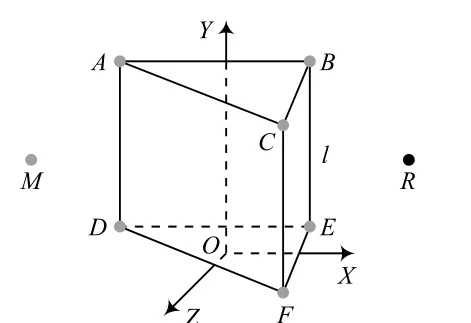
图2 信标节点“三棱柱”分布模型

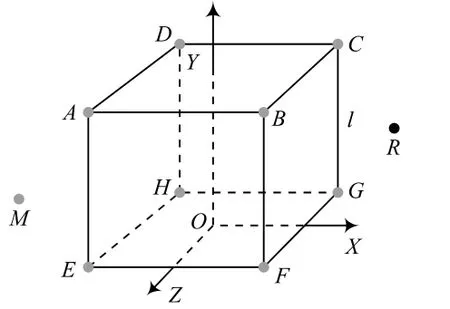
图3 信标节点“四棱柱”分布模型

在上述三图中，A，B，C，D，E，F，G，H均为信标节点，M是任一待定位节点，R是终端用户节点。待定位节点M周期性地发送包含自身信息的无线信号至信标节点，信标节点接收待定位节点发送的无线信号后，解析出该节点的身份标识，并测定接收到的信号强度指示RSSI，根据RSSI测距公式[8]计算出待定位节点到此信标节点的距离，然后把这一距离和待定位节点的身份标识发送至终端用户节点R。终端用户节点R根据信标节点发送的距离信息计算出待定位节点的坐标。

1.2 立体定位算法

建立三维直角坐标系，标定信标节点在直角坐标系中的位 置 坐 标 A（x1，y1，z1），B（x2，y2，z2），C（x3，y3，z3），D（x4，y4，z4），E（x5，y5，z5），F（x6，y6，z6），G（x7，y7，z7），H（x8，y8，z8），假设待定位节点M的坐标为（x，y，z）。用di（i=1，2，…，8）表示待定位节点到信标节点的距离。具体研究中，通常使用的RSSI定位模型如下[8-10]：

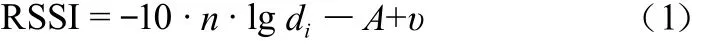
式中：A为信号距离为1 m时，接收信号的功率（dBm）；n为信号传输常数，与信号的传输环境有关；di为发射节点到信标节点的距离；υ服从（0，δ2）高斯分布，为零均值的随机测量噪声，表示环境对数学模型影响的程度。文献[4]中提到，通过实验证明，v对距离的计算结果影响不大，因此本文去除υ，用简化后的信号传输模型来估计距离。

用（xi1，yi1，zi1），（xi2，yi2，zi2），（xi3，yi3，zi3） 和（xi4，yi4，zi4）表示图1～图3三个信标节点分布模型中任意一组不在同一平面上的四个信标节点坐标，di1，di2，di3和di4分别表示待定位节点到此四个信标节点的距离，则任一待定位节点坐标（x，y，z）满足如下关系：

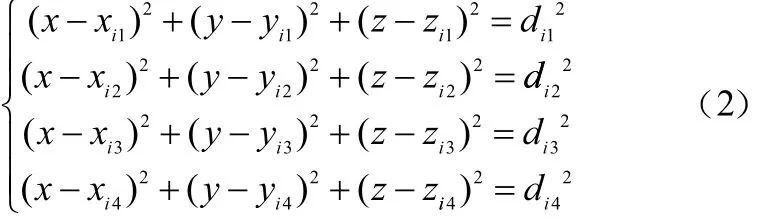
用式（2）中的第1～3个方程减去第4个方程，并表示成线性方程的形式AX=b，其中：

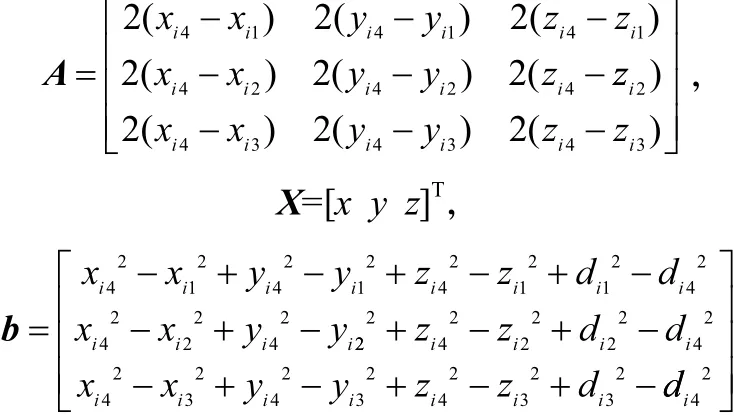
在AX=b两边同乘A－1得到X=A－1b，即待定位节点坐标为（x，y，z）。

需要注意的是，在图1所示的信标节点分布模型中，一共有四个信标节点，只可得一个如式（2）所示的方程组，所以只能计算得到一个待定位节点的坐标。而在图2和图3所示的信标节点分布模型中，信标节点的数量分别为6个和8个，可得到多个如式（2）所示的方程组，可由此计算得到多个待定位节点的坐标。在实际应用时，可根据需要取其均值，作为待定位节点的坐标。

2 实验设计

2.1 实验环境

信号RSSI在不同环境下对应的距离曲线不同，因此我们搭建了如下实验环境来进行距离曲线实验。

上述无线传感器网络节点选用网蜂科技有限公司生产的ZigBee模块，实物如图4所示，其核心芯片为CC2530。

测试场地选在物联网实训实验室，如图5所示。

图4 实验节点

图5 测试场地

2.2 实验方法和结果

实验时，发送节点和接收节点离地高度均为0.5 m，并保持天线垂直于地面，发送节点和接收节点为直视链路，且每隔0.5 m测量接收到的RSSI值。在发送节点和接收节点距离为1 m时，实验测得的接收信号功率A=41 dBm。通过两组信号强度-距离测试数据，利用（1）式计算得到n=2.3。把所有的测试数据进行4次Matlab曲线拟合，得到信号强度对应的距离曲线如图6所示。

3 定位仿真

3.1 信标节点间距对定位精度的影响

本节利用图1所示的“三棱锥”分布模型探索在室内环境中，信标节点间距对定位精度的影响。定位精度用平均定位误差表示[11-12]，平均定位误差的定义如下：

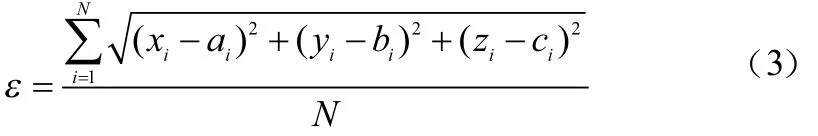
式中 ：（xi，yi，zi）是计算得到的待定位节点的坐标 ；（ai，bi，ci）为实际坐标；N为测试次数。

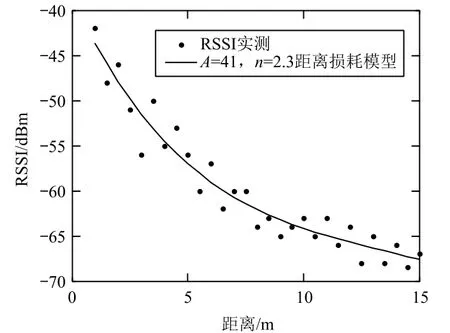
图6 信号强度对应的距离曲线

仿真步骤如下：

（1）设定图1“三棱锥”模型中信标节点的间距l，计算每个信标节点在坐标系中的坐标，4个信标节点的坐标分别为

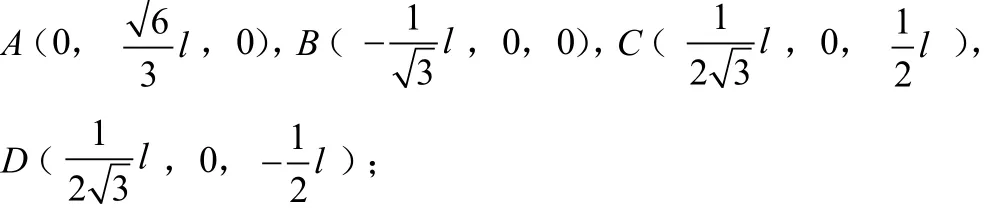
（2）当移动节点处于不同位置时，位置坐标用（ai，bi，ci）表示，分别计算移动节点到4个信标节点A，B，C，D的距离：

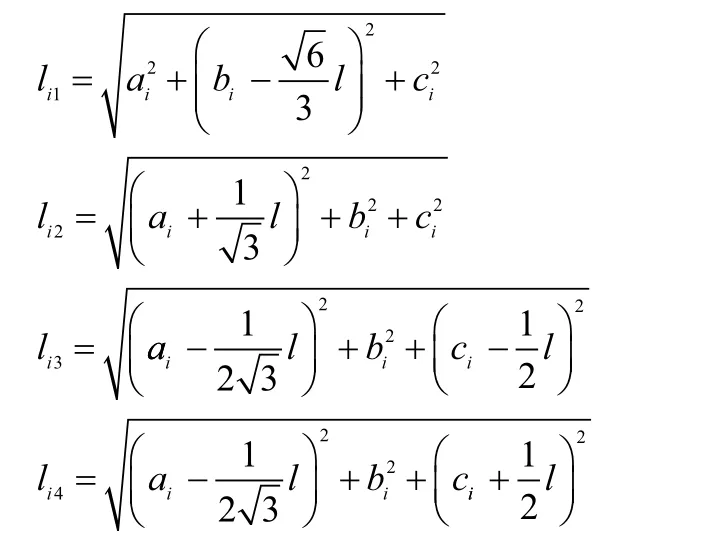
（3）根据步骤（2）得到的移动节点到信标节点的距离，在图6所示的距离损耗模型中标定对应的信号强度RSSI；

（4）根据步骤（3）标定的RSSI，利用公式（1）计算移动节点到每一个信标节点的距离di；

（5）根据步骤（4）得到的移动节点到每一个信标节点的距离 di，利用公式（2）计算移动节点的坐标（xi，yi，zi）；

（6）将步骤（5）计算得到的移动节点坐标（xi，yi，zi）和移动节点的实际坐标（ai，bi，ci）代入公式（3），计算得到平均定位误差。

按照上述步骤，利用Matlab2014进行仿真，仿真结果如图7所示。

从图7的仿真结果可以看出，平均定位误差随着信标节点间距的增加而减小。当信标节点间距为1 m时，平均定位误差为1.8 m；当信标节点间距为5.5 m时，平均定位误差为1.38 m。当采用“三棱锥”分布模型，信标节点间距为5.5 m时，比信标节点间距为1 m时的平均定位误差减小了0.42 m。

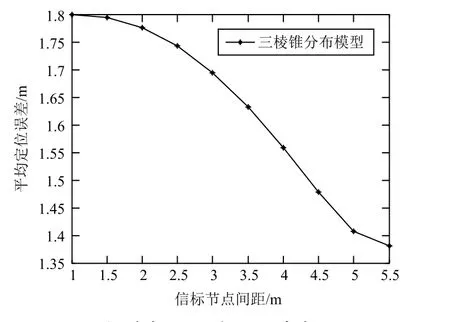
图7 信标节点间距对定位精度的影响

3.2 信标节点分布模型对定位精度的影响

按照和“三棱锥”分布模型相类似的仿真步骤，当信标节点按“三棱柱”模型和“四棱柱”模型分布时，分别对定位精度进行仿真。

需要注意的是，“三棱柱”模型和“四棱柱”模型中，信标节点的数量分别为6个和8个，可得到多个如式（2）所示的方程组，由此得到多个待定位节点的坐标。所以，在利用（3）式计算时，可得到多个平均定位误差值。把这多个值取算术平均，得到图8所示的仿真结果。

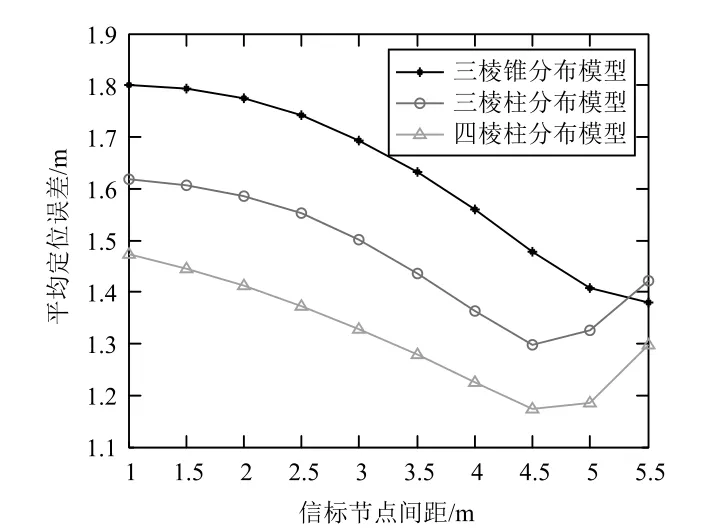
图8 信标节点分布模型对定位精度的影响

从图8所示的仿真结果可以看出，当信标节点的分布模型为“三棱柱”模型和“四棱柱”模型时，定位精度会随信标节点间距的增加而提高。当信标节点间距为4.5 m时，“三棱柱”模型和“四棱柱”模型的平均定位误差最小，分别为1.3 m和1.17 m。从信标节点的三种分布模型来看，“四棱柱”模型性能最优，“三棱柱”模型次之，“三棱锥”模型最差。当信标节点间距一定时，“四棱柱”模型的定位精度比“三棱柱”模型的定位精度高约10%，而“三棱柱”模型的定位精度又比“三棱锥”模型的定位精度高约10%。之所以得到这样的结果，是因为“三棱柱”模型中信标节点的数量是6个，“四棱柱”模型中信标节点的数量是8个，两者分别比“三棱锥”模型多出了2个和4个信标节点。所以，定位精度的提高是以多付出的信标节点设备为代价的，这与常见的无线传感器网络定位理论相一致。

此外，可由图8所示的仿真定位误差曲线看出，采用“三棱柱”模型和“四棱柱”模型，且当信标节点间距大于4.5 m时，平均定位误差反而会随着信标节点间距的增大而增大。所以，通过本文的仿真可知，定位精度并非完全随着信标节点间距的增加而提高。在实际应用中，选取合适的信标节点间距十分必要。

可采用“三棱柱”模型和“四棱柱”模型，当信标节点间距大于4.5 m时，为了减小平均定位误差，对算法进行优化：“三棱柱”模型和“四棱柱”模型中，信标节点的数量分别为6个和8个，计算时，会有多个如式（2）的方程组，由此计算得到多个待定位节点的坐标。在利用（3）式计算时，可得到多个平均定位误差值。一旦某个平均定位误差高于某值，就会舍弃这一组数据。经过优化后的仿真结果如图9所示。

经优化后，“三棱柱”模型和“四棱柱”模型的平均定位误差最小值分别为1.15 m和1.05 m，比优化前分别小了0.15 m和0.12 m。

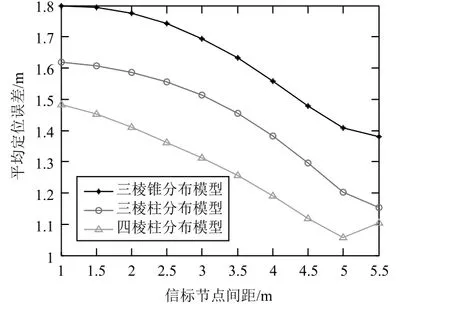
图9 优化后的仿真结果

4 结 语

本文提出了信标节点可移动的无线传感器网络立体定位算法。建立了三种信标节点的分布模型——“正三棱锥”分布模型、“正三棱柱”分布模型和“正四棱柱”分布模型，仿真了不同信标间距对定位精度的影响，以及信标节点分布模型对定位精度的影响。仿真结果表明，本文提出的立体定位算法能准确定位待定位节点的相对位置坐标。本算法将在室内定位、物品追踪等领域有较广阔的应用前景。