岩石薄片显微图像采集自动聚焦方法

陈旺，滕奇志，何海波，苏桂芬

（1.四川大学电子信息学院图像信息研究所，成都610065；2.成都西图科技有限公司，成都 610065；3.国土资源实物地质资料中心，三河 065201）

0 引言

岩石薄片是地质勘探中获得的宝贵实物资料，通过光学显微镜对岩石薄片进行矿物鉴定是石油地质行业的常规手段，而显微成像为薄片的数字化保存、信息共享以及图像处理分析提供了条件。

在显微镜下进行薄片图像采集，一次只能得到一个小视域的图像，要得到完整的全薄片图像，需要通过载物台移动，逐视场采集并将图像拼接起来。在切换视场的过程中，由于岩石薄片无法达到绝对的平整，因此要求在切换视场后，通过调整载物台的高度对物距进行调整，保证采集图像清晰。

在当前的聚焦系统中，分为主动式聚焦和被动式聚焦两种[1]。主动式聚焦不仅硬件繁杂，而且很容易出现因焦距测量不准确导致聚焦失败。目前主流采用的聚焦方式为被动式聚焦，该方式通过分析相机实时捕获的画面清晰度，对图像质量做出评价，通过移动载物台，使之呈现出清晰画面示意到达焦点[2]。

1 聚焦算法设计

相机捕捉画面形式为图像，其模糊状态下和清晰状态下所含纳的信息量具有显著差异，在描述图像信息含量时，通常采用图像梯度的方式，图像梯度表示当前像素与相邻像素的差异情况，梯度越大，图像表现为边缘更明显，包含信息量更大；梯度越小，表示该像素处于图像的平滑区域，包含信息量越少[3]。因此，可以根据图像的梯度信息含量作为图像聚焦状态的参考值。通过调整载物台的高度使之达到清晰度最高的点，达到聚焦的目的。

1.1 清晰度评价函数

聚焦准确的前提是所选择的清晰度评价函数能够判断当前图像清晰与否，优秀的清晰度评价函数，其曲线应具备单峰、陡峭、准确、平滑等特性[4-5]。清晰度评价函数的工作通俗意义上就是将视觉上图像的感官清晰与否以数值高低的形式表现出来。以下为常用的清晰度分析方法[6]。

（1）时域分析法。时域分析法主要是获取原始图像的梯度信息，根据梯度数值大小示意细节丰富程度。常用的时域分析法主要有Sobel函数、灰度差分绝对值之和函数法、Robert函数法、灰度方差函数法等。

（2）频域分析法。频域分析法原理是将图像进行傅里叶变换或小波变换，依据其能量分布，设置下限频率，通过累计高频能量值的多少，从而判断清晰度。

（3）信息熵分析法。信息熵分析法是基于香农理论，通过对原始图像进行信息熵的计算，判断图像清晰度，通常信息熵越大，图像越清晰。

通常，时域分析法较频域分析法、信息熵分析法更具优势。小波变换和傅里叶变换等频域分析法计算量大，空间梯度通过相邻像素灰度值的简单计算即可获得，而熵函数灵敏度较低，根据图像内容差异可能出现与实际情况相反的结果。

本文采用Sobel函数作为清晰度评价函数，该函数采用Sobel算子对原始图像水平和垂直方向进行边缘信息量提取，并累计梯度信息，计算出清晰度值。

假设采用内核为3的Sobel算子提取图像梯度分量：

（1）横向梯度：

式中，F(x,y)为待进行边缘提取的图像，Gx(x,y)为与横向Sobel算子卷积后的临时结果图像。

（2）纵向梯度：

式中，F(x,y)为待进行边缘提取的图像，Gy(x,y)为与横向Sobel算子卷积后的临时结果图像。

（3）近似梯度：

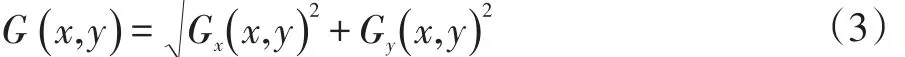
式中，Gx(x,y)，Gy(x,y)为待进行边缘提取的图像，G(x,y)为综合横向、纵向边缘梯度提取后的结果图像。

（4）清晰度评价函数：

式中，D为清晰度计算结果，M为图像宽度，N为图像高度，G(x,y)为综合横向、纵向边缘梯度提取后的结果图像。

1.2 聚焦区域与爬山对焦

在聚焦过程中，需选取一定的区域作为清晰值计算的来源。区别于全景聚焦，选取部分区域作为清晰度计算区域可以大大降低计算量，有效提高清晰度值的计算效率[2]。

聚焦区域选取目前主要采用1D区域选择、中心取窗区域选择、多点取窗区域选择、非均匀采样等主流算法[7]，对于颗粒信息丰富的岩石薄片，采用以上方法均能取得良好效果，但是，在实际应用中存在大量目标稀疏的薄片，而选取固定位置进行单点聚焦往往无法包含颗粒信息而造成误判，导致聚焦不准确甚至聚焦失败。

针对以上问题，本文采取多点聚焦的方法，单独对每一区域进行清晰度值计算，选择清晰度值最大的两个位置，其结果求和作为最终清晰度值。空白区域不含目标颗粒，而光线波动加重了清晰度评价函数曲线的毛刺现象，经大量实验分析，同一薄片，其空白区的清晰值不高于该薄片目标颗粒区清晰值的1/3，利用这种特性，可判断出该位置是否空白，从而在聚焦过程中有效规避空白区域。

如图1所示，本文选择四个位置进行多点聚焦，若四个位置计算后清晰度值依次为D1，D2，D3，D4且D1>D2>D3>D4。根据本文算法，最终清晰度值为V=D1+D2。

图1 聚焦位置

聚焦算法中，最主要的三个部分为：聚焦区域选择、清晰度评价函数设计、峰值点搜索策略[8]。选择聚焦区域与清晰度评价函数后，合理设计搜索策略尤为重要。

传统的搜索策略采用固定步长爬坡聚焦，首先试探性垂直移动载物台固定距离，再根据移动前后清晰度值对比，可判断出正确的搜索方向，再使用爬坡法搜索焦点。

具体算法如下：

（1）计算当前位置清晰值V1，载物台试探性向下移动固定步长，计算移动载物台后视场的清晰值V2；

（2）比较载物台移动前后的清晰度值，若清晰度值增大，则按原方向移动载物台固定步长，若清晰度值减小，则按原方向的反方向移动载物台固定步长；

（3）重复步骤2，直至载物台移动出现反转。

在薄片的制造过程中，受限于制作工艺，薄片往往存在局部不平整的情况，通常，在切换视场后需重新搜索新市场的焦点，如下图2所示，受光线波动的影响，清晰度评价函数曲线存在大量毛刺，该毛刺的存在可能导致聚焦不准确甚至聚焦失败，尤其是切换视场后，当前位置偏离新市场焦点较远时，清晰度评价函数曲线在该点附近较为平缓，毛刺影响显著，移动的步长过小使得聚焦陷入局部极值，导致聚焦失败；而在焦点附近，移动步长过大使得聚焦不准确，偏离焦点较远甚至成像模糊聚焦失败。因此在实际设计搜索算法时，不能采取固定单一步长进行聚焦，聚焦步长需根据当前偏离焦点的多少具有可变性：离焦点较远时，采用大步长进行聚焦；离焦点较近时，采用小步长进行聚焦[9-10]。

图2 清晰度评价函数曲线

观察清晰度评价函数曲线上升（下降）段，曲线呈现出明显拐点，该拐点可反映出曲线斜率的增减。对于实际聚焦过程，测绘完整的清晰度评价曲线寻找拐点准确位置不仅耗时，而且繁琐。数学上拐点的定义给予我们灵感，当曲线从“凹增”变化为“凸增”时，其割线斜率从增大变化为减小。计算割线斜率只需记录聚焦过程载物台移动前后其清晰度值及移动步长。通过判断割线斜率的增长（减小）趋势，能够大致得到拐点范围，从而选择合适的步长进行聚焦。

以曲线上升段为例，拐点以左，斜率增大；拐点以右，斜率减小。在斜率增大的区间段，此时偏离焦点较远，宜采用大步长进行焦点的搜索；在斜率减小的区间段，此时已接近于焦点，宜采用小步长进行精确搜索。

具体算法如下：

（1）计算当前位置清晰值V1,载物台试探性向下移动固定步长，计算移动载物台后视场的清晰值V2；

（2）比较载物台移动前后清晰度值V1、V2：

若V1>V2,则往上移动载物台同等固定步长，并记录移动后的清晰度值V3,若|V3-V1|>|V2-V1|,采用大步长进行聚焦，反之，采用小步长进行聚焦；

若V1＜V2，则往上移动载物台同等固定步长，并记录移动后的清晰度值V3,若|V3-V2|>|V2-V1|,采用大步长进行聚焦，反之，采用小步长进行聚焦。

（3）按传统爬坡法进行焦点搜索，当清晰度值增减由急升变为平缓时，改用小步长。

2 实验结果分析

为了体现本文算法的优势，选取岩石颗粒较为稀疏的视场进行聚焦。实验采用偏光显微镜，载物台垂直方向电机精度0.001㎜，设置单次步长0.01㎜。相机分辨率3456×2304，程序基于VS2010平台开发实现，假设视场长度为W，高度为H。

本文算法选取计算范围如下：

位置1起点（2*W/15,H/4）

位置1终点（11*W/30,7*H/20）

位置2起点（19*W/30,H/4）

位置2终点（13*W/15,7*H/20）

位置3起点（2*W/15,13*H/20）

位置3终点（11*W/30,3*H/4）

位置4起点（19*W/30,13*H/20）

位置4终点（13*W/15,3*H/4）

计算面积占视场面积7/75,聚焦面积占视场面积7/150。

采用不同的清晰度评价函数，其边缘检测效果不同，本文对比拉普拉斯函数、Sobel函数、双线性滤波Sobel函数法、灰度方差函数法、Robert函数法，定向移动载物台，使用多种算子计算图像清晰度，绘制清晰度评价函数曲线如图3。

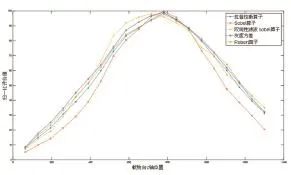
图3 不同算子清晰度评价函数曲线

从图像上看，基于拉普拉斯算子、Sobel算子、灰度方差、Robert算子的清晰度评价函数均具有良好的无偏性，经双线性滤波后的Sobel函数其峰值偏离焦点较远，以上清晰度评价函数均满足单峰性要求，相比于其他清晰度评价函数，基于Sobel算子的清晰度评价函数更为灵敏且存在明显的拐点，适宜于本文搜索策略，能够达到快速聚焦的目的。

3 结语

本文所提出的基于Sobel算子多点聚焦算法虽然存在波峰较宽的不足，但具有良好的无偏性、单峰性、快速性，特别是在目标颗粒不均匀的情况下，比传统的聚焦算法具有更加优秀的抗噪性能。结合基于斜率变化的变步长搜索策略，本文的自动搜索算法可以实现岩石薄片显微图像采集的自动聚焦。