二维平面网络渗流模型最大集团的相变研究

蔡 静，孔嘉勇，张 新

（佛山科学技术学院物理与光电工程学院，广东佛山528000）

渗流模型指的是分布在空间内相邻或者相连的点的一系列集合，点与点之间的联系通常通过两种关联方式来实现，一种是点的位置和点与点之间的关联是随机的，另外一种是点的位置已经确定，而点与点之间的关联要通过某种特定且随机的规则来实现。

渗流模型多用于研究多孔介质中的输运问题[1]，亦可用与许多自然界中实际问题的理论模型，如流行病传播[2]、森林火灾[3]、介质和导体混合物的传导特性[4]等。渗流是一种几何模型，其规则虽看似简单，但蕴含着深刻的物理意义。这类应用领域中的实际问题虽然规则相对简单，但是对于研究热力学统计物理的相变和临界现象有着重要的参考价值，因此吸引了很多学者的广泛兴趣。

ACHLIOPTAS等人提出最小乘法规则[5]（Product rule，简称PR规则），并在规则网络和无标度网络等网络中进行了研究。2009年，ROBERTM.Ziff研究了二维正方网络上动力学渗流的爆炸性生长，且采取了只将键放置在不同的集团之间。这样一来限制条件更加严格，此规则下的渗流相变点延迟到0.9925 附近[6]。

1 渗流

1.1 渗流模型

渗流模型根据占据对象不同可分为位点渗流（Site percolation）和键渗流（Bond percolation），以BOLLOBÁS[7]1998年著作中的内容来解释规则图形的渗流。设有图形Λ，V（Λ）和E（Λ）分别代表其中位点和键的集合。点渗流中的位点以一定的概率p被占据，用被占据表示导通，未被占据表示不导通，相邻导通的点的集合组成同一个集团；键渗流中，相邻位点的键以一定概率p被占据，相邻导通的键以及所有的点组成同一个集团。如图1所示。

图1 点（Site）渗流和键（Bond）渗流

图1a表示二维正方网络Zd上的点渗流，图中用空心点表示不导通的点，用实心点表示导通的点，一个集团包含所有相邻导通的位点；图1b表示键渗流，集团的形成是通过键将实心点连接起来实现的。如果整个格子中出现从左至右或者从上至下的一条通路，使得至少有一个方向是导通的，这个时候就说网络实现了渗流。如图1a的点渗流，网络尺寸为5×5，初始的时候网络上不放置点，可以定义从网络的左下方开始，以概率p放置实心点，以概率1-p放置空心点，放置完25个点。相邻的实心点从属于同一个集团Sx，通过统计实心点的数目来计算集团的大小。图中1a是取概率p=0.7时的单次模拟结果，此图中一共形成了ns=4个相互独立的集团，可以统计出4个集团中，有一个实心点数目为9的集团，称之为最大集团Smax。图1b的键渗流，第一步用实心点填充网络上的每个位点，仍然从网络的左下角开始，取概率p放置键，通过键相连接的实心点属于同一个集团，取概率1-p不放置键。单次模拟后形成了ns=6个集团，其中最大集团包含了5根键。可以想象，当p值很小无限接近于0时，几乎不会出现渗流；当p很大无限接近于1时，网络几乎都处于渗流状态。介于这两种情况，即当p为一特殊值时，使得网络刚好达到状态转变，此时的p就是发生相变的临界值pc。

根据热力学概念，在热力学极限下，当概率达到临界值pc时，网络中便会出现一个宏观尺度的渗流集团，这个时候渗流系统会以连续的相变（二阶相变）的形式出现。或者可以这样表示：总存在一个临界值 pc∈[0，1]，当 p＜pc时，P（p）=0；而当 p＞pc时，p=pc，此时系统处在临界状态，其中 P（p）=0 代表没有实现渗流，P（p）＞0代表至少有一个集团实现了渗流。

1.2 爆炸性渗流

如前所述，ROBERTM.Ziff对ACHLIOPTAS等人的模型进行了微小的规则改动，得到了新的二维平面正方网络爆炸性渗流。规则如下，在添加键时，随机选取两条备选键e1和e2，根据最小乘积规则（productrule，PR）来选取键，即将e1和e2连接的集团相乘，乘积最小者被选中。如图2所示，e1集团大小的乘积为2×7=14，e2集团大小的乘积为4×4=16。通过比较显然e1将被留下而e2将被舍弃。但是，如果此时的e1是属于同一集团内部的，那么就要放弃此次的操作，重新选择新的e1和e2。由于此规则优先合并小尺寸集团，那么整个系统中所有集团的尺寸会趋向于均匀，导致最大集团的形成得到了延迟。但当无限接近相变点的时候，每添加的一根键都会引发最大集团尺寸的急剧增加，且发生的时间极其短暂，呈现一种爆发性的相变，即现在所说的爆炸性渗流的形成[8]。

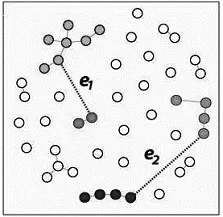
图2 PR规则下集团演化示意图

1.3 渗流的临界指数

渗流模型中，由于周期性边界条件，当集团趋于无限大时，在网络中任意选择一个位点，定义位点属于无限大集团的概率为 P∞。渗流相变的临界值记为 pc，当 p＜pc时，P∞=0；p＞pc时，P∞≠0。P∞在 pc附近满足幂率关系

其中β就是临界指数，把这种p非常接近pc时渗流的表现叫做渗流的临界行为。

每个位点（键）必然存在如下3种可能状态：1）以概率为1-p不被占据；2）以概率为p（1-P∞）属于其他有限大集团；3）以概率为p·P∞属于无限大集团的一部分。所有位点（键）属于任意一个集团的概率为ps=s·ns，概率总和为

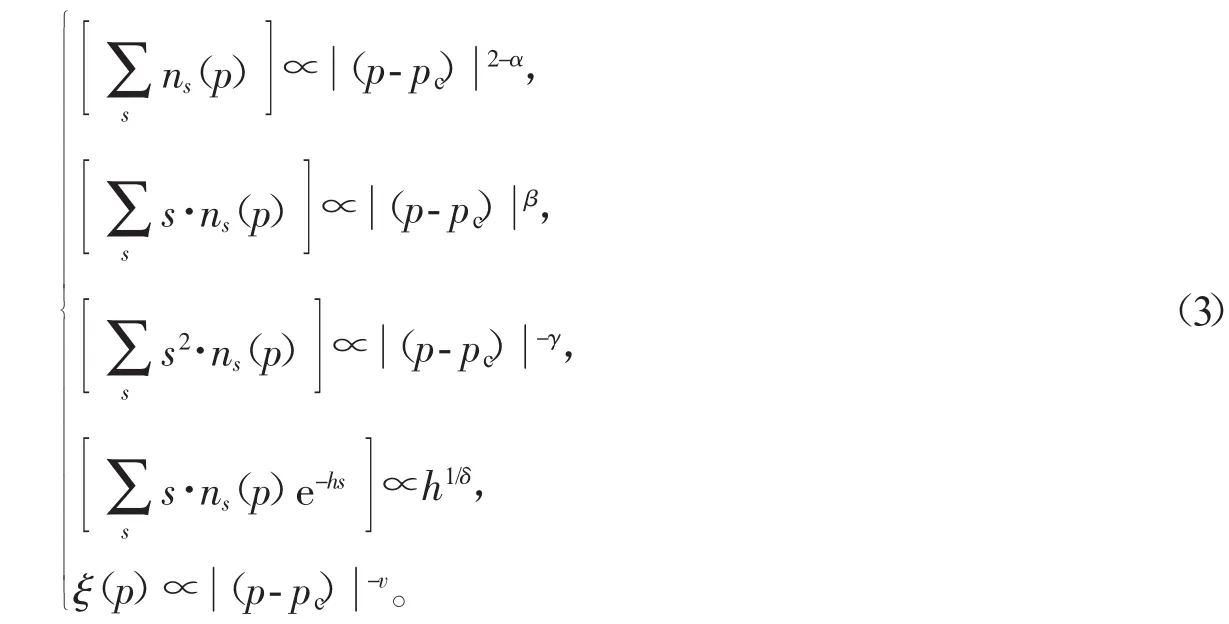
对式子两边取对数，以ln（p-pc）为横坐标，ln（P）为纵坐标作图，每个式子的临界指数即为该图的斜率。6个普适临界指数α、β、γ、δ、η、ν以及热临界指数yt和磁临界指数yh之间满足一定的标度关系[9]

利用计算机拟合出yt和yh后再计算求得其他临界指数。

1.4 本文所用规则

总结本文所用规则如下：

（1）初始化二维正方网络，每个位点都是一个大小si=1的独立集团；

（2）随机选择两个位点 i1、i2，且 i1≠i2，再分别随机选择各自的邻点 j1、j2；

（3）计算集团乘积大小 P1=si1·sj1、P2=si2·sj2；

（4）对 P1、P2的大小进行比较，如果 P1＜P2，则用一根键 bond1 连接 i1和 j1；如果 P1＞P2，则用另一根键bond2连接i2和j2；如果P1=P2，则bond1和bond2被选中的概率均为0.5；

（5）合并集团；

（6）重复以上（1）到（5）步，直至所有键都已成功放置到网络中[7]。

2 最大集团尺寸

对不同尺寸的网络分别执行了100万次的全格点计算，得到二维正方网络的/N-p关系曲线如图3a所示，其中 N=L×L。用 5种颜色对不同尺寸进行区分，L=16（红色），32（绿色），64（蓝色），96（紫色），128（黑色）。

对最大集团归一化后的数值通过（4）式进行拟合，得到相应的临界点和临界指数

其中 ai、ci都是相应的系数，pc是临界值，d=2，c0为临界点最大集团平均尺寸，c0=0.72（2）。

在临界点附近对进行拟合，拟合得二维正方网络的临界值pc=0.523 8（2）。根据（5）式的有限尺度的标度行为，做临界点处的ln/N-ln L关系图，如图3b所示，二维正方网络曲线的斜率-β/v=-0.059（1）。临界指数 yt=0.51（2），yh=0.90（5），ν=1.00（3），γ=1.90（3），η=0.10（1），α=-0.02（2），β=0.07（4），δ=2.05（7）。

图3 /N与p的关系和ln/N与ln L关系

3 结论

最大集团尺寸由于规则限制，增长较为缓慢，当接近临界点附近，最大集团尺寸爆发性地增长，相应图像曲线呈阶跃性跳变，且网络尺寸越大，这种爆发性增长越明显。