一类带σ边值条件的脉冲微分方程解的存在性

阴少辉

（广东工业大学应用数学学院，广东广州510520）

脉冲方程比不含脉冲项的微分方程能更精确地反映部分自然规律，一些脉冲微分方程模型很好地说明了这个事实[1-2]。研究包含边值条件的脉冲微分方程问题[2-10]的主要方法有Leray-Schauder定律、上下解的方法、锥拉伸与压缩不动点定律和单调迭代方法。

ChenYuqing等[6]研究过下面在有限维空间中包含边值条件的脉冲方程反周期解的问题

如果满足以下条件：

本文将在不要求G满足Lipschitz条件的情况下，研究如下一阶包含σ边值条件的脉冲微分方程的解是否存在

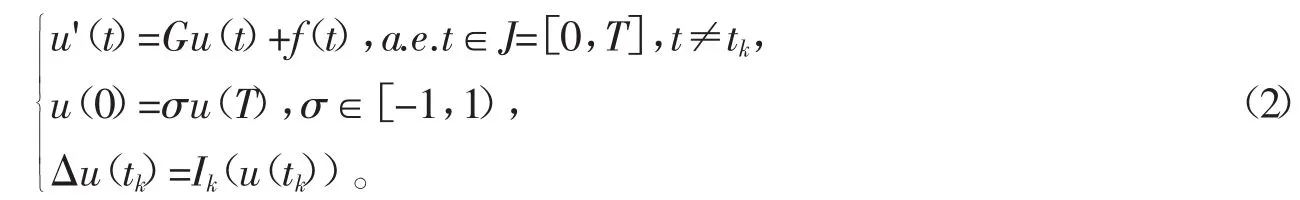
1 预备知识

先介绍以下符号

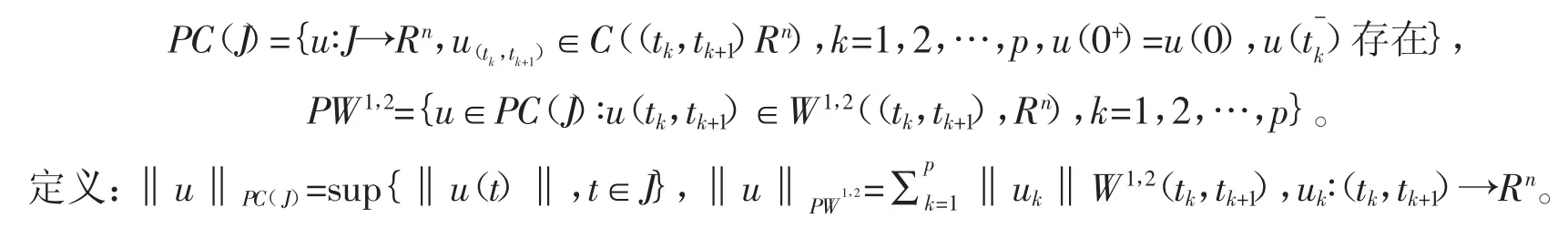
引理1 Ii∶Rn→Rn是连续的，i=1，2，...，p，对任意的xk∈Rn，，其中 α，δ为大于0的常数。假设满足，则有

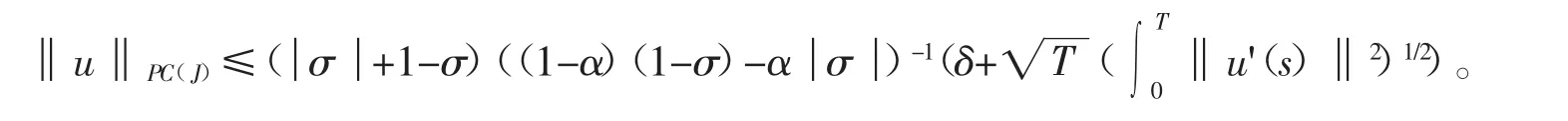
证明 由条件得

于是

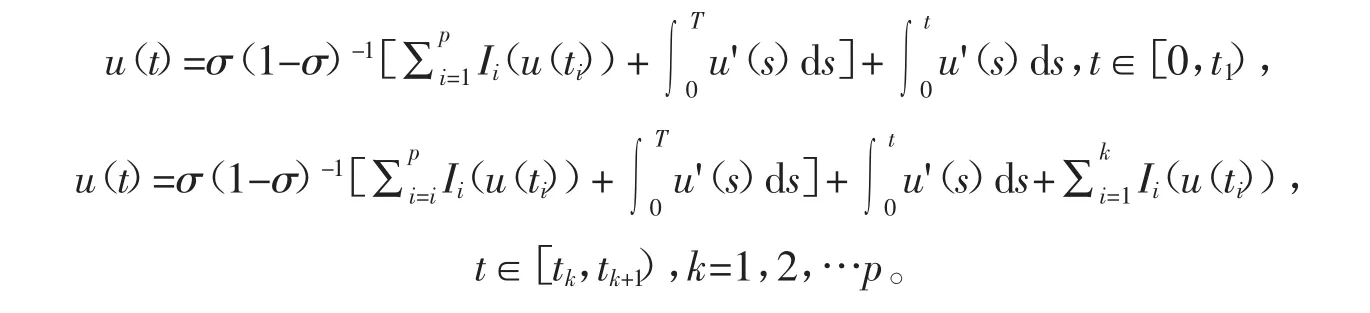
所以

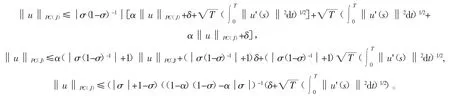
2 主要结论

定理1若G∶Rn→Rn是连续的是连续的。如果满足以下条件：

则方程（2）有解。

证明 由引理1，对于任意的v∈PC（J）可考虑下面的方程

显然方程（3）有如下唯一解

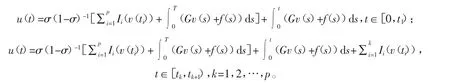
（I）证明K是连续映射。

因为G是连续的，vn→v，n→∞，由控制收敛定理得到

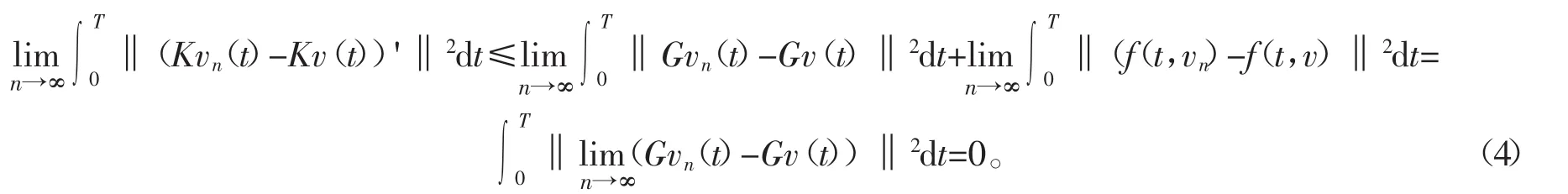
当 t∈[0，t1）的时候，有

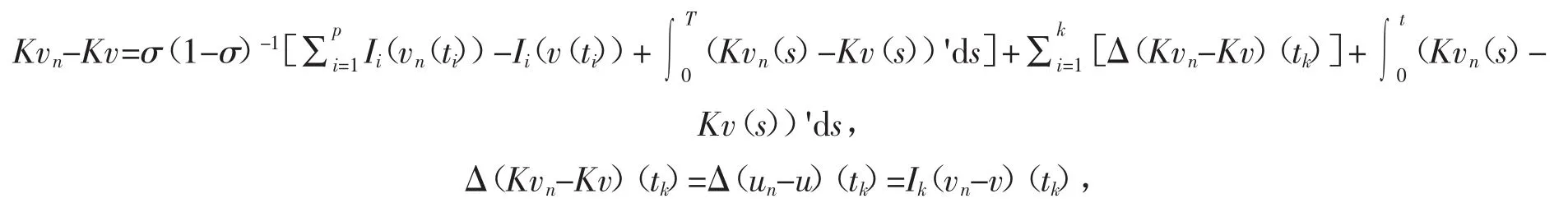
Ik是连续的，以及式（4）得 K 是连续的。

（II）证明K是紧映射。

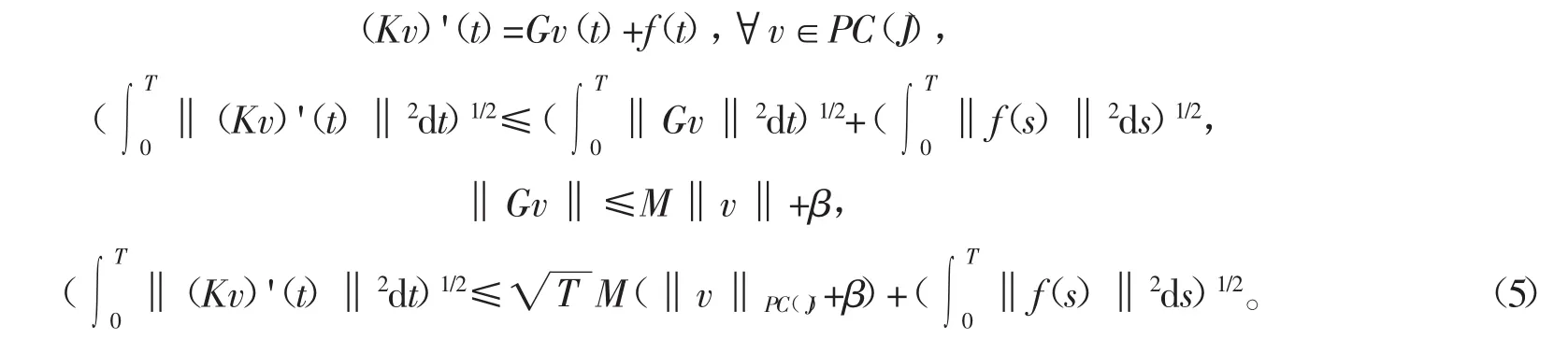
（IV）证明对∀λ0∈（0，1），满足v=λ0kv的所有 v是有界集。

若存在 v∈PC（J），v=λ0kv，λ0∈（0，1），满足

易见

其中，t∈[tk，tk+1），k=1，2，…，p。

所以

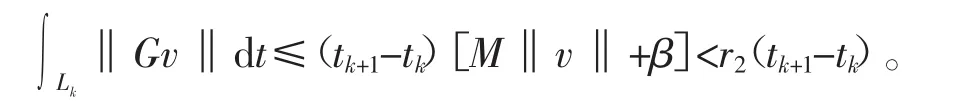
在 t1，t2，…，tp这些点上，单点积分为 0，舍去它们，有

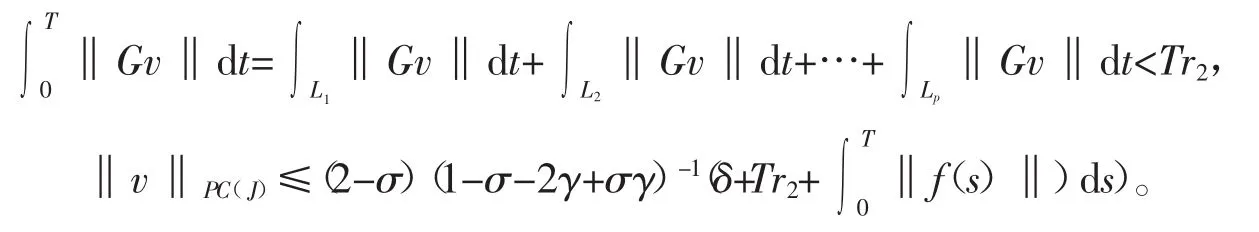
由Leray-Schauder二择一定理得方程（3）有解。

利用类似于定理1的方法可得到如下结果。

定理2若G∶Rn→Rn是连续的，f（t，x）∶[0，T]×Rn→Rn为Caratheodory函数，，g（t）∈L2（[0，T]），Ii∶Rn→Rn是连续的，k=1，2，…，p。

如果满足下面条件：

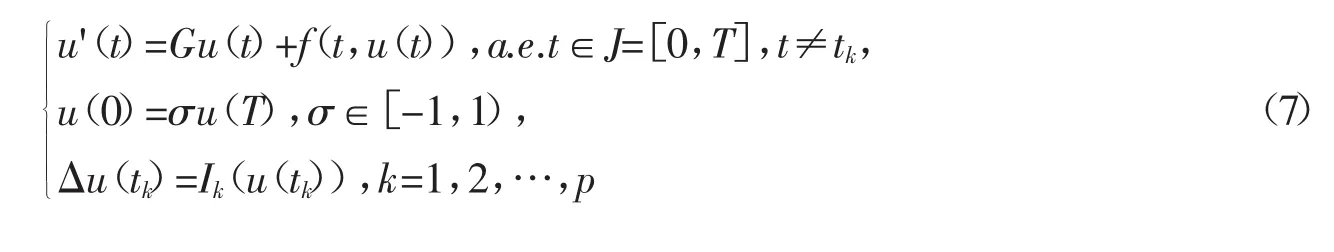
有解。

注 当σ=-1时，本文所研究的问题即为文献[6]反周期边值问题.

3 实例

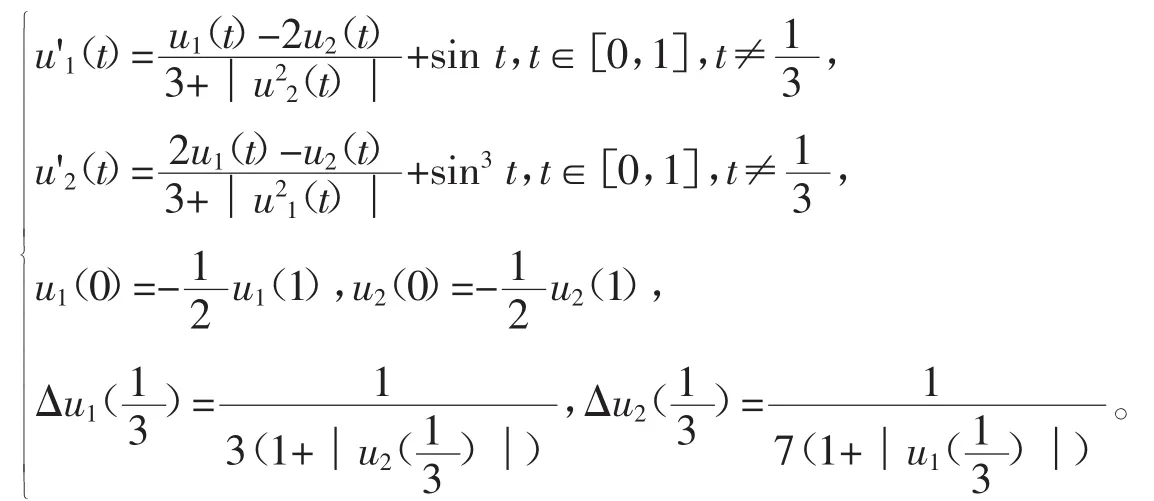
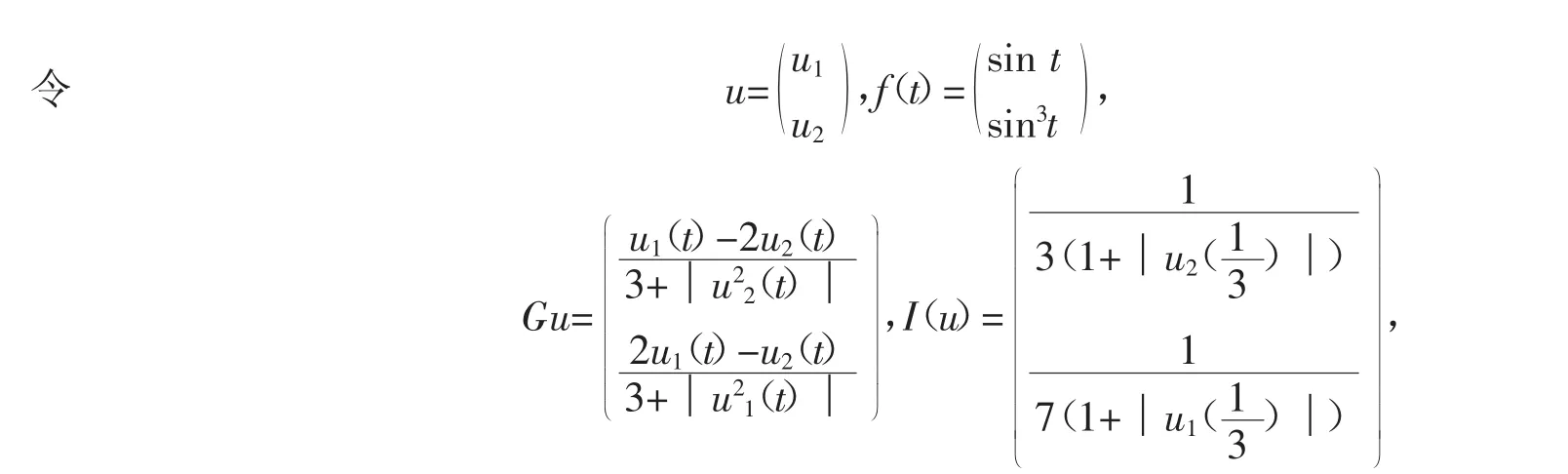
方程等价于

显然方程（8）满足定理1的所有条件，因此方程（8）有解。