废水处理过程中BOD5与CODcr相关关系分析研究

武蔼娜

(山西汾西矿业集团环境监测有限责任公司，山西 介休 032000)

引 言

水污染的两个重要评价指标是化学需氧量(CODcr)和五日生化需氧量(BOD5)，可以用来反映废水的生物化学性能和废水处理装置的处理效率。其中，化学需氧量(CODcr)是指在强酸条件下用强氧化剂并加热，将废水中的有机物还原为无机物所消耗的氧化剂的量。其测试方法简单，可以在1.5 h～2.0 h内测试出结果。五日生化需氧量(BOD5)是指水中有氧条件下有机物在微生物作用下分解所需的溶氧量，直接反映了废水中可生化有机物含量。BOD5被广泛采用作为描述废水可生化性及处理效果的指标，但该参数需要在(20±1) ℃条件下对水样稀释培养5 d才能测定，且受到水中营养条件及菌种的干扰不能及时反映废水处理情况[1]。因此，研究废水处理中BOD5与CODcr的相关关系，根据测定的CODcr值来推导BOD5值，可以建立以CODcr为废水特征指标的废水处理系统，提高监测效率。

1 测定方法

1.1 CODcr的测定

化学需氧量的测定方法选择重铬酸钾回流法进行测定，即，在强酸条件下，加入过量重铬酸钾标准溶液和适当催化剂，加热2 h，将水样中的还原性物质氧化，过量的重铬酸钾以试亚铁灵作为指示剂，回滴标准硫酸亚铁铵溶液，根据重铬酸钾标准溶液的消耗量计算出CODcr值。具体计算公式见式(1)。

(1)

式中：V0为空白消耗硫酸亚铁铵标准体积，mL；V1为水样消耗硫酸亚铁铵标准体积，mL；V水为水样体积，mL；c为硫酸亚铁铵标准浓度，mol/L。

1.2 BOD5的测定

五日生化需氧量的测定方法选择稀释与接种法，水样稀释后在(20±1)℃下培养5 d，求出培养前、后溶解氧含量的差值，结合稀释倍数计算BOD5值，具体计算公式见式(2)。

(2)

式中：D1为培养液在培养前的溶解氧，mol/L；D2为培养液在培养5 d后的溶解氧，mol/L；B1为接种稀释水在培养前的溶解氧，mol/L；B2为接种稀释水在培养5 d后的溶解氧，mol/L；f1为接种稀释水在培养液中所占的比例；f2为水样在培养液中所占的比例。

2 相关性研究

2.1 线性方程建立

从第196页表1的数据统计可以看出，废水中的CODcr和BOD5含量在一定时期内比较稳定，其中，废水处理一厂的废水来源为A地区生活废水，废水中CODcr为42 mg/L～67 mg/L，BOD5为9.9 mg/L～16.4 mg/L，BOD5与CODcr的比值在0.25左右；废水处理二厂的废水来源为印染企业A废水，废水中CODcr为54 mg/L～84 mg/L，BOD5为16.3 mg/L～26.7 mg/L，BOD5与CODcr的比值在0.33左右。

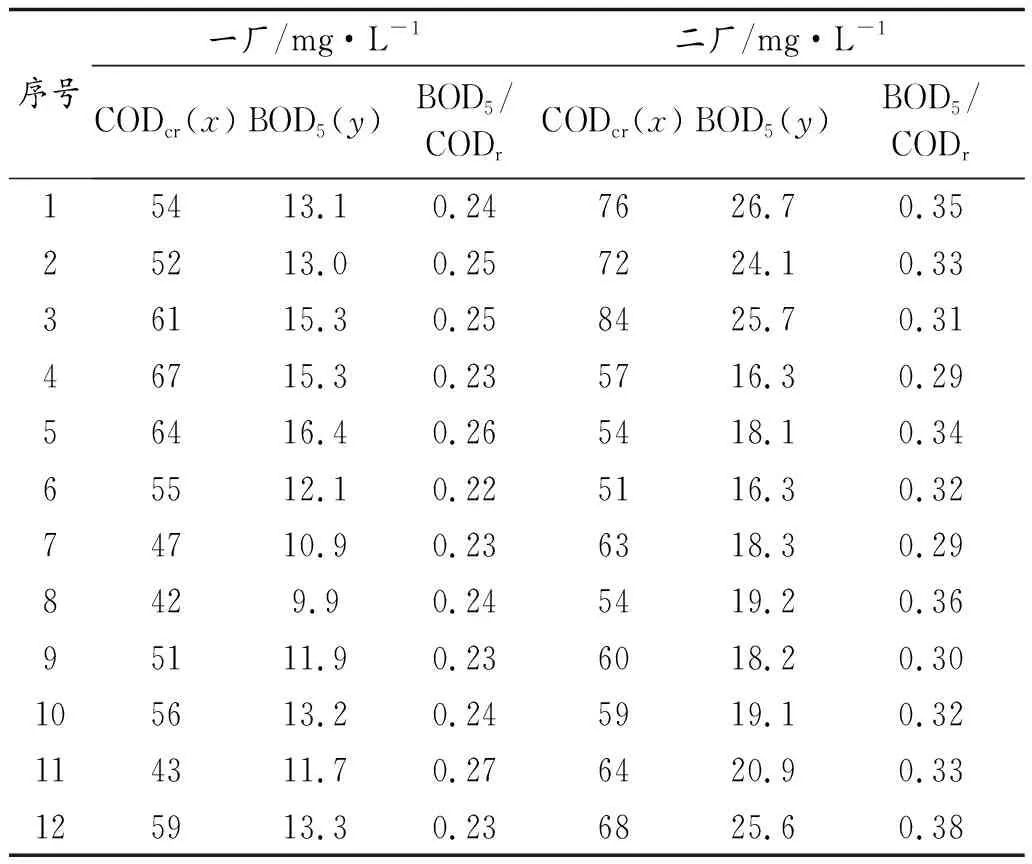
表1 监测数据统计表

通过对表1的数据进行分析，在废水来源基本稳定的情况下，废水中的有机物组成没有太大变化，CODcr和BOD5存在一定关系，可以通过建立CODcr和BOD5的线性回归方程找到二者间的相关关系[2]。

设CODcr和BOD5的线性方程为BOD5=aCODcr+b，其中，a、b为常数。对表1中的数据利用最小二乘法进行分析，见式(3)、式(4)。

(3)

(4)

式中：x为CODcr值，y为BOD5值，n为数据组数。将表1中废水处理一厂和二厂的数据分别带入式(3)和式(4)中，可以求得a1=0.223 2，b1=0.901；a2=0.340 7，b2=-0.923 4，即，废水处理一厂中生活废水CODcr和BOD5的相关关系为：

BOD5=0.223 2CODcr+0.901

废水处理二厂中印染厂废水CODcr和BOD5的相关关系为：

BOD5=0.340 7CODcr-0.923 4

2.2 线性回归方程检验

线性回归方程建立后，还需要对方程的规律性进行检验，是否可以利用该方程通过CODcr值对BOD5值进行预测，线性回归的检验方法是通过相关系数和T检验来进行相关性和显著性检验的。

相关系数r是以变量对均值的离差为基础，通过积差计算，反映两个变量的相关关系，r的取值范围在-1～1，正、负号表示变化趋势同向或反向，|r|的大小表示相关程度，越接近1表示相关关系越密切，见式(5)。

(5)

式中，x为CODcr值，y为BOD5值，n为数据组数。将表1中废水处理一厂和二厂的数据分别带入式(5)中，可以求得，r1=0.916 1，r2=0.888 4，可知两种废水中的CODcr和BOD5均为正相关。

T检验中的t值可由相关系数求得，见式(6)。

(6)

将相关系数r1=0.916 1、r2=0.888 4、n=12带入式(6)，求得t1=7.23，t2=6.12。由于CODcr和BOD5是正相关关系，故进行单侧检验，当显著性水平为0.01时，自由度为10，查t值表得t0.01(10)=2.764。可以看出，t1、t2均大于t0.01(10)，所以，CODcr和BOD5正相关具有显著意义，线性回归方程成立。

2.3 预测结果检验

通过实测的CODcr值利用已进行检验的线性回归方程对废水中的BOD5值进行预测，与实测的BOD5值进行比较，结果见表2。

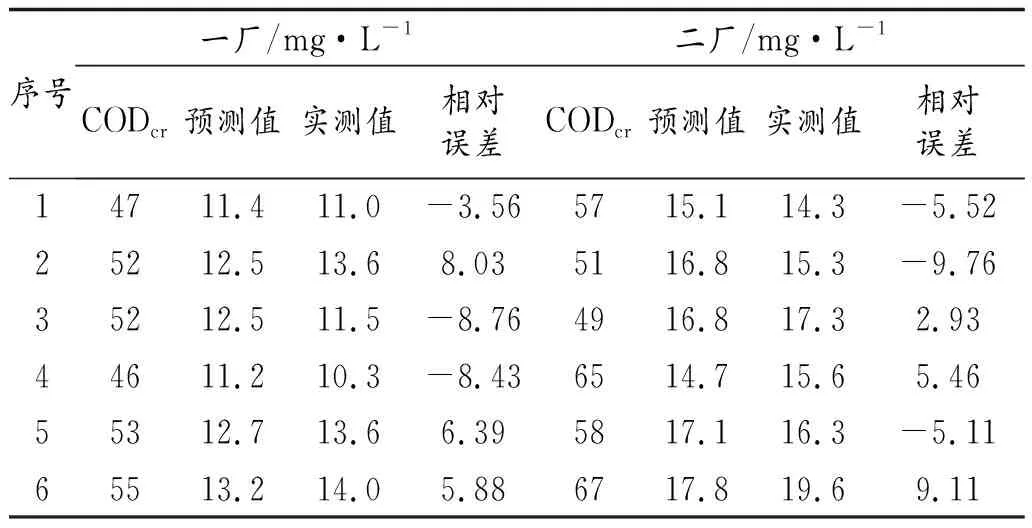
表2 BOD5实测值与预测值对比

从对比结果可以看出，一厂废水中BOD5实测值与预测值的最大相对误差为8.76%，平均相对误差为6.8%；二厂废水中BOD5实测值与预测值的最大相对误差为9.76%，平均相对误差为5.3%，预测的精确度均在±10%以内，验证了该预测方法的有效性。

3 不同来源废水分析

通过上述分析可以看出，废水来源稳定时CODcr和BOD5存在相关关系，本文继续对不同废水处理厂来源不同的废水进行检测分析，建立线性回归方程，研究CODcr和BOD5间的相关关系。

3.1 印染企业B的废水

对同处A地区的印染企业B的废水采样，进行水质分析，使用同样的方法建立线性回归方程描述CODcr和BOD5间的相关关系，其结果如图1所示。

图1 印染企业B废水中CODcr和BOD5的相关关系

从结果可以看出，印染企业B废水中CODcr和BOD5也存在相关关系，线性回归方程为BOD5=0.229 2CODcr+1.225 8，相关系数r=0.996 9，T检验中t=31.0，经查表知该方程相关性显著。与印染企业A废水中的CODcr和BOD5线性回归方程进行对比，印染企业A和印染企业B虽然同为印染行业，但线性回归方程确有很大不同，主要原因是两企业的工艺水平、原料来源等有所差别，造成废水中有机物组分及含量不同。

3.2 B地区生活废水

对B地区的生活废水采样，进行水质分析，使用同样的方法建立线性回归方程描述CODcr和BOD5间的相关关系，其结果如图2所示。

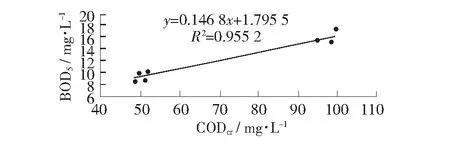
图2 B地区废水中CODcr和BOD5的相关关系

从结果可以看出，B地区生活废水中CODcr和BOD5也存在相关关系，线性回归方程为BOD5=0.148 6CODcr+1.795 5，相关系数r=0.977 3，T检验中t=11.3，经查表知该方程相关性显著。与A地区生活废水中的CODcr和BOD5线性回归方程进行对比，两者虽然同为生活废水，但线性回归方程不同，主要原因是，两个地区的生活条件、饮食结构不同，造成废水中有机物组分及含量不同。

3.3 造纸厂废水

对同处A地区的造纸厂废水采样，进行水质分析，使用同样的方法建立线性回归方程描述CODcr和BOD5间的相关关系，其结果如图3所示。

从结果可以看出，B地区生活废水中CODcr和BOD5也存在相关关系，线性回归方程为BOD5=1.358 7CODcr+471.33，相关系数r=0.953 2，T检验中t=7.72，经查表知该方程相关性显著。对比造纸厂废水与印染企业废水和生活废水中CODcr和BOD5间的线性回归方程可以看到，斜率与截距的差别很大，造纸厂的方程斜率最大，说明造纸厂的废水中可生化降解的有机物含量较大，从而使有机物进行生物化学过程中消耗溶解氧的量偏高。

图3 造纸厂废水中CODcr和BOD5的相关关系

4 结论

使用科学的检测方法对水质采样进行分析检测，记录水样中CODcr和BOD5的检测数据，根据检测结果建立了CODcr和BOD5的线性回归方程，并验证其有效性，得出了以下结论：

1) 在废水来源单一并且稳定的情况下，废水中CODcr和BOD5存在相关关系并且关系密切，在生产实践中可以根据测定的CODcr值利用建立的线性回归方程对BOD5值进行预测，其结果可靠，能够用于指导废水处理过程，可以适度减少BOD5的监测频度，提高生产效率，建立以CODcr为废水特征指标的废水处理系统。

2) 同行业中不同企业的废水中CODcr和BOD5的相关关系由于企业的生产工艺水平、生产类别、原料来源的不同会产生差异，不能使用同一线性回归方程描述CODcr和BOD5间的相关关系，应注意平时监测数据的分析和累积，对回归方程进行修正。

3) 不同行业中的废水中CODcr和BOD5相关关系不同，线性回归方程的斜率、截距、相关系数均不同，应根据行业的不同、CODcr和BOD5相关关系不同选择具有针对性的废水处理系统。