基于随机抽样一致性算法的风电机组塔筒倾斜度检测方法

雷阳，兰维，石超，张中泉，刘勇钊

(1.杭州职业技术学院 友嘉机电学院，杭州 310018； 2.华电电力科学研究院有限公司，杭州 310030；3.浙江省工程物探勘察院，杭州 310005)

0 引言

风能是一种安全、清洁、可再生的新能源，发展风能等新能源成为世界各国的共识[1]。近几年，在政策引导和价格补贴等手段的推动下，全球风电快速发展。截至2017年年底，全球风电累计装机容量已经达到539.58 GW，其中，中国大陆风电装机容量达到188.23 GW[2]。

近年来，随着风电行业的快速发展，由于设计缺陷、制造问题以及检查和维护不充分导致风电事故频繁发生。典型的事故有风电机组倒塌、着火、超速飞车、叶片断裂、频繁脱网等[3-5]。风电机组主要部件包括塔筒、叶片、机舱、轮毂、发电机、齿轮箱等[6]，其中塔筒起到支撑整个机组的作用，因此，当发生塔筒倾斜、折断等导致机组倒塌时，由此引起的经济损失是巨大的。塔筒安装完毕后，后期对它的检测、监测是避免事故发生的一个重要措施[3,7]。塔筒倾斜度的检测是塔筒检测的一项重要指标，通常利用全站仪等设备对塔筒进行数据采集，然后利用各类科学计算方法对数据进行整理、计算，从而得出塔筒倾斜度，最后参照标准判断是否合格。

1 测试背景与方法

1.1 测试地点与设备

本研究所使用的数据均采集自甘肃省酒泉市瓜州县某风电场，共采集到8台金风GW82/1500型风电机组的塔筒倾斜度数据。数据采集设备为徕卡TCA2003全站仪，采集时间为2018年3月15—18日，累计4 d。

1.2 测试流程

(1)以风电机组为坐标原点，分别在120°夹角位置均布3个基准点，且基准点距离风电机组1.5D～2.0D(D为风电机组塔筒的高度)，并形成闭合导线点网。

(2)测量时将仪器架设在基准点上，使用极坐标法对风电机组塔筒顶部和底部两个位置进行观测。其中底部观测点为基础环与第1节塔筒连接沿处，顶部观测点为机舱与塔筒交界处。

(3)根据三点圆的数学原理，计算得出塔筒顶部和底部圆心及其偏差，利用相关公式得出倾斜度。

为保证结果的准确性，在每个基准点至少对塔筒不同位置进行2次以上观测。观测时遵循以下原则：(1)观测时采用独立的坐标系统；(2)根据平面控制测量要求观测；(3)严格按GB 50026—2007《工程测量规范》和JG J8—2007《建筑变形测量规范》的要求，始终遵循先控制后测量原则，做到每次测量成果均符合限差要求；(4)观测时环境条件基本一致。

1.3 利用最小二乘法拟合圆心坐标

测试完成后，采集到的塔筒倾斜度观测数据点分布情况如图1所示。传统方法是使用最小二乘法对塔筒倾斜度数据进行拟合，从而得到圆心坐标。

假设利用最小二乘法所拟合得到的圆曲线方程可表示为：

R2=(X-A)2+(Y-B)2，

(1)

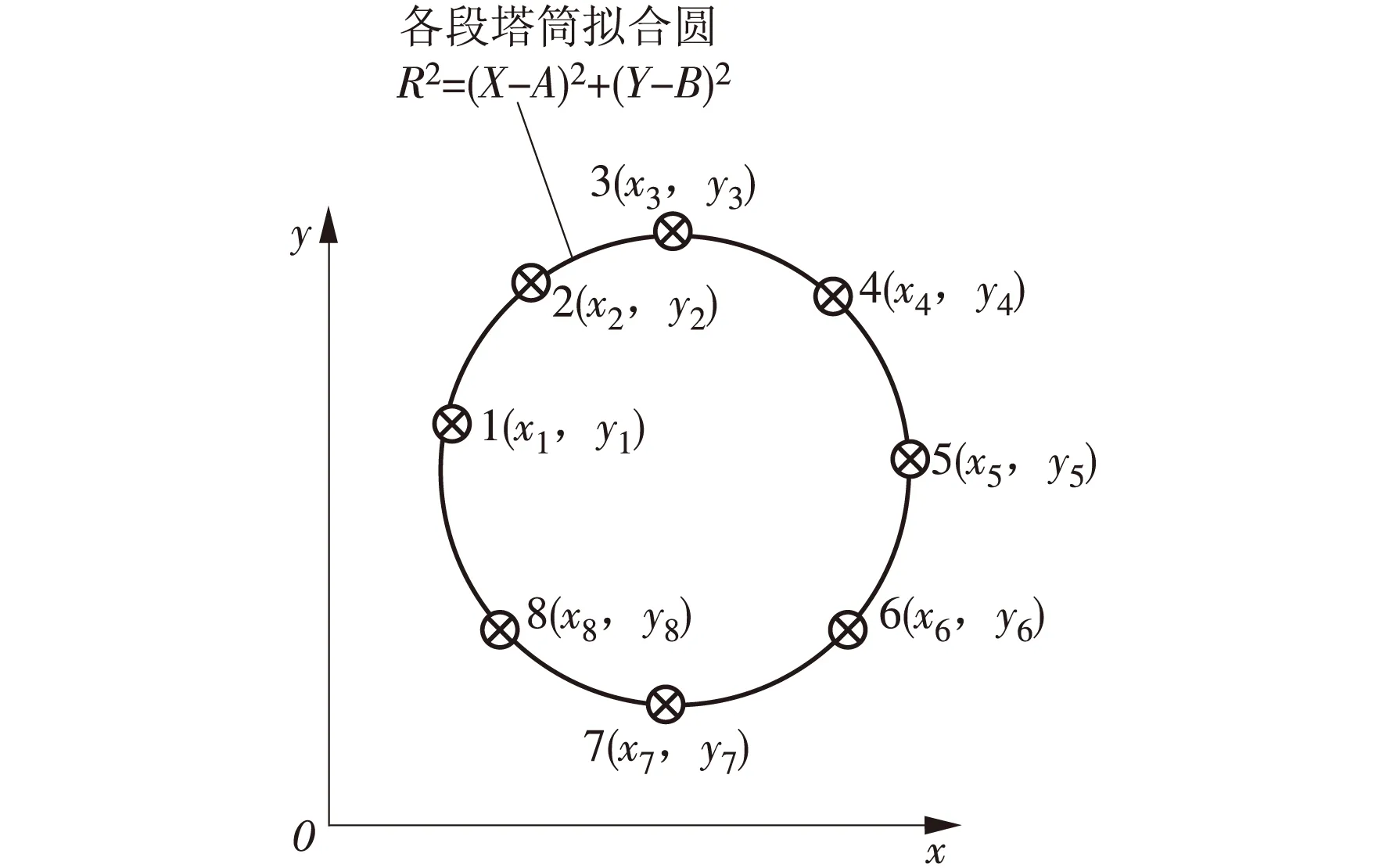
图1 采集到的数据点分布示意

式中：R为拟合圆的半径；X为数据在x轴上的坐标值；Y为数据在y轴上的坐标值；A为拟合圆心在x轴上的坐标值；B为拟合圆心在y轴上的坐标值。

令a=-2A，b=-2B，c=A2+B2-R2，可得到圆方程

X2+Y2+aX+bY+c=0 ，

(2)

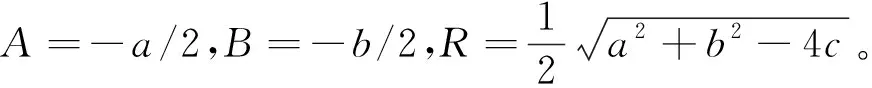
测试完成后得到样本集(xi，yi),i∈(1,2,3，...，N)，点(xi，yi)到圆心的距离记为di，

di2=(xi-A)2+(yi-B)2，

(3)

那么，点(xi，yi)到圆的距离的平方和与半径平方和之间的差可表示为

δi=di2-R2=(xi-A)2+(yi-B)2-R2=

xi2+yi2+axi+byi+c，

(4)

令P(a，b，c)为δi的平方和

P(a，b，c)= ∑δi2=∑(xi2+yi2+

axi+byi+c)2，

(5)

求参数a，b，c，使得P(a，b，c)的值最小。

对式(5)进行求偏导，可得到极值点，比较所有极值点，最后得到最小值。

byi+c)xi=0 ，

(6)

byi+c)yi=0 ，

(7)

byi+c)=0 。

(8)

解上述方程组，令C=(N∑xi2-∑xi∑xi)，D=(N∑xiyi-∑xi∑yi)，E=N∑xi3+N∑xiyi2-∑(xi2+yi2)∑xi，F=(N∑yi2-∑yi∑yi)，G=N∑xi2yi+N∑yi3-∑(xi2+yi2)∑yi，可解得

Ca+Db+E=0 ，

(9)

Da+Fb+G=0 ，

(10)

(11)

(12)

(13)

即可求得A，B，R的估计拟合值。

利用最小二乘法可准确拟合出圆心坐标，但当出现测试人员操作失误、测试设备异常等情况时，数据点可能存在异常点(如图2所示)，此时利用最小二乘法拟合圆心点坐标，所得值可能跟实际情况存在较大差异，最终导致检测的精度较低。

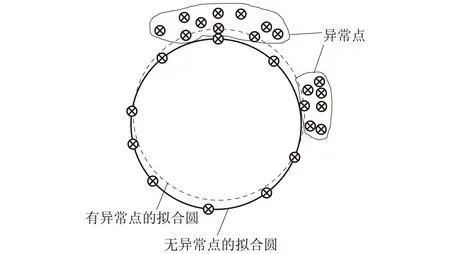
图2 存在异常点的数据集

为解决传统利用最小二乘法存在异常点导致检测精度低的问题，本文提出一种基于随机抽样一致性的风电机组塔筒倾斜度检测方法。

1.4 随机抽样一致性算法

随机抽样一致性(RANSAC)算法[8]在处理数据时具有较大优势，其特点是从一组包含“局外点”的检测数据集中，通过迭代的方式来估计数学模型的参数。随机抽样一致性的基本假设有：(1)数据由“局内点”组成；(2)“局外点”不能适应已知模型的数据；(3)其他数据为噪声数据。图3为随机抽样一致性算法的基本流程[9-10]。

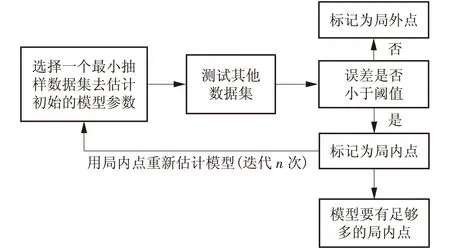
图3 随机抽样一致性算法基本流程

随机抽样一致性算法需确定的参数有：判定局内点的阈值t、迭代次数n、使得模型合理的局内点个数mx。在估计模型的参量时，用p表示迭代过程中从数据集内随机抽取的点均为局内点的概率，用q表示每次从数据集中抽取一个局内点的概率。

q=mx/M，

(14)

式中：M为数据集的个数。

假设估计模型时需要m个点，则qm表示为m个点都为局内点的概率；那么(1-qm)则表示至少一个点是局外点的概率。(1-qm)n表示算法不会选择到m个点都是局内点的概率，其等于(1-p)，即表示1-p=(1-qm)n。对该公式取对数可得到迭代次数n的公式

(15)

阈值t一般靠经验选取，其直接影响局内、局外点的判断[10-11]。假如阈值t选择较小，算法太过敏感，导致放弃部分有效点；若阈值t选择较大，算法不敏感，对有效数据可能造成误判。本文使用平均绝对偏差F来估计数据的方差，以解决该问题。若选取的数据子集为yi，则表达式为

F=Averagei(|(yi-Averagej(yi))|) ，

(16)

式中：Averagei为求数组中的均值函数；|·|为求绝对值的符号；i和j分别为数据子集的位置。

阈值t表示为测试数据的平均绝对偏差，再用模型去测试剩余的数据，假如数据点到圆的距离小于t，则认为该点是局内点，反之就是局外点。已有学者验证了随机抽样一致性比最小二乘法具有较好的可靠性和稳定性[10,12]，本文不再赘述。

2 结果与分析

利用随机抽样一致性算法计算得到每台风电机组塔筒上下圆心坐标，再根据建筑物基础的倾斜值S的计算公式，可计算出塔筒的倾斜度。

(17)

式中：ΔL为位移量；H为监测圆心点面间距。

此次试验的风电机组塔筒高度为67.8 m，通过式(17)可计算出各风电机组塔筒的倾斜率，见表1。

从表1可看出，塔筒倾斜率最大的是E3-5F风电机组，达0.001 234。GB 50007—2011《建筑地基基础设计规范》标准规定，多层和高层建筑的整体倾斜率应小于0.002 5(60 m<自室外地面算起的建筑物高度≤100 m)，由此可见，此次测得的各风电机组塔筒倾斜值均符合规范要求。

虽然此次检测的8台风电机组倾斜率均合格，但理论上塔筒的变形是动态的，故建议在恶劣天气运行期间，需再次对各风电机组进行监测，比较风电机组前后倾斜率是否稳定，保证风电场的安全、稳定运行。

3 结论

本文依托甘肃瓜州某风电场试验数据，利用平均绝对偏差方法剔除异常点，并利用随机抽样一致性算法计算每台风电机组塔筒上下圆心坐标。结果显示，基于随机抽样一致性算法能够较好地应用于风电机组塔筒倾斜度检测中。