某导引头电子模块力学特性分析*

段柳浠，汪 奕，芮 棽

(南京电子技术研究所， 江苏 南京 210039)

引 言

导弹和航天技术是当今国防科技中发展最为关键的技术领域之一，同时也是在电子机械方面高新科技最为密集的领域之一[1]。导弹技术的存在使得军事思想和作战方式都发生了重大变革。随着导弹和反导技术的不断交替发展和制衡，导引头正朝着小型化、精密化、功能复合化的方向发展[2]。特别是近10年我国在大规模集成电路、相控阵天线、信号处理等领域的飞速发展和革新给导引头设计带来了诸多新的思路，在丰富导引头的体制和设计方向的同时对于导引头的结构环境适应性也提出了更高和更为全面的要求[3]。

弹载导引头在导弹发射和巡航过程中会受到诸多不同类型的外界载荷影响，发射时承受短时大量级的冲击，巡航中由于高速旋转会承受高量级的各向过载，针对复杂且苛刻的环境条件，采用传统的力学验证试

验不仅成本高，效率低而且影响研制周期，因此采用有限元分析做结构设计的补充辅助手段能够成倍的缩短设计时间，过程高效且成本低廉。

本文根据弹载的特殊力学环境特点，对某导引头中针对性设计的一个电子模块组件进行了有限元模型建立、静力学和动力学分析，得到了在加速、冲击、随机振动环境下结构的变形、加速度和应力数据，与设计阈值对比从而达到检验校核该模块结构刚强度的目的[1]。

1 有限元分析模型

建立符合实际结构，边界条件吻合实际使用情况的有限元分析模型是进行准确的计算机力学仿真的前提。本文从模型简化、材料设定、网格划分等几个方面详述有限元模型的建立过程。

1.1 模型建立与简化

力学分析对象为某导引头复杂阵面结构中重要的电子模块，具有结构复杂，材料不一，且质量分布不均匀，细节特征较多等结构特点。如图1所示，该模块主要包括金属材质馈线、金属支撑结构板、印制板、多种陶瓷类及塑料零部件等。

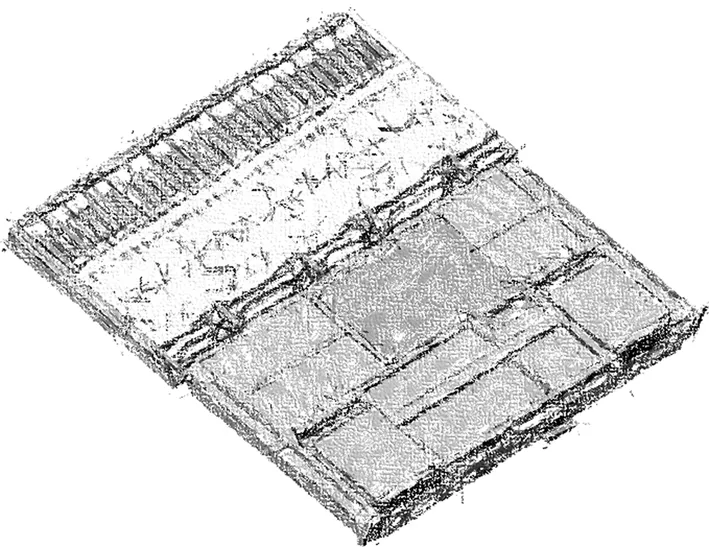
图1 电子模块结构示意图

有限元分析计算的耗时通常与模型划分网格数、单元类型等信息息息相关，特别是网格数量甚至直接决定计算时间长短。在现有普通计算机的计算能力有限的情况下，遵循合理简化原则对结构进行精简对于减小工程计算规模、提高计算效率是至关重要的。

简化的原则通常是：首先，需保证质量分布尽可能接近真实情况，采用改变局部网格的材料密度可以达到在兼顾网格规则划分的情况下质量可以真实分配；其次，部分对计算结果影响较小的局部细节特征、过于复杂的结构可根据实际情况进行相应的简化或等效替换。如螺纹孔一般可简化为光孔处理。为了进一步减小计算量，小孔径的孔也可以按照无孔等效。圆角、倒角可按直角处理以规则网格排布。

由此可见，二甲双胍能有效地延缓AS的进展，对T2DM患者心血管系统具有一定的保护作用。但由于受伦理道德原则、《药物临床试验质量管理规范》（GCP）和相关法律法规的约束，目前该方面临床研究还相对较少，其结论仍有待进一步验证。

按照上述精简原则对模型进行了处理后的有限元模型如图2所示。具体简化方法如下：1)金属材质馈线与金属支撑结构板之间的螺钉连接采用刚性单元RIGID[4]来模拟；2)反面集成电路元器件用小质量等效点来替换；3)金属支撑结构板的部分凸台去除，安装螺纹孔也做去除处理；4)金属材质馈线内嵌的辐射元件通过改变馈线该区域密度来等效模拟[5]；5)校核各部分质量值及质心分布，保证简化的模型总质量等效且各部分质心分配与真实情况一致。

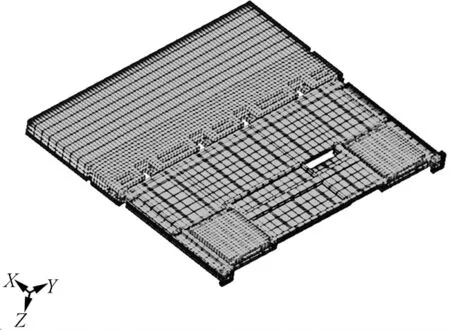
图2 电子模块有限元模型

1.2 单元属性赋予

该电子模块的有限元模型主要采用了Hex8单元和Penta6单元，共12 332个体单元，20 222个节点。节点及单元数目在计算机承受范围以内。

该电子模块的零部件材料主要为5A05铝合金以及聚四氟乙烯SFBN-1，其基本力学性能参数如表1所示。

表1 主要材料力学参数表

1.3 边界条件

该电子模块在导引头中的安装固定情况为：

1)模块底部两侧对称布置有两法兰，分别通过4颗M3螺钉固定到导引头主承力框架上；

2)模块底部中间位置对称布置有两颗销钉，通过与导引头框架销孔配合定位。

根据该模块实际安装情况对有限元模型施加约束，如图3所示：

1)在该导引头电子模块底部两侧的螺钉安装处施加全约束边界条件；

图3 边界条件约束示意图

2 力学仿真计算

2.1 模态分析

在力学分析中，模态分析除了获取结构的固有频率以外还可以验证模型与实际结构及边界条件的吻合性。此外进行多阶模态分析的计算结果可以为以模态叠加为计算方式的随机振动仿真计算提供频域数据输入，达到压缩计算时间的目的。模态分析提取的固有频率和振型云图如表2及图4所示。

表2 模态分析结果

图4 模块模态振型图

2.2 正弦振动分析

释放约束点x方向平动自由度，在所有约束点上施加对应x方向的加速度载荷，对结构进行x方向频响分析。

将正弦振动荷载条件施加到结构上，得到：结构加速度最大值响应为4.51g，对应频率为100 Hz；结构应力最大值响应如图5所示，最大应力为0.25 MPa，对应频率为100 Hz。

图5 正弦振动应力云图(100 Hz)

分析结果如表3所示。加速度响应与鉴定级输入条件4.5g对比，基本持平，无明显响应放大现象。按照安全系数取1.5且遵循3σ应力进行校核，仿真结果表明结构设计满足正弦振动试验要求。

表3 正弦振动分析结果

2.3 随机振动分析

本文随机振动分析取鉴定级作为输入条件，释放约束点一个方向平动自由度，该自由度分别对应x、y、z三个方向加速度荷载，对结构进行随机振动分析，分析结果如表4和图6所示。

表4 随机振动分析结果

图6 z向随机振动应力云图

x、y、z三个方向随机振动应力最大值为13.9 MPa，方向为z向，同样按照安全系数取1.5且遵循3σ应力进行校核，仿真结果表明结构设计满足随机振动试验要求。加速度最大值为53.1g，方向为z向。加速度响应与鉴定级输入条件12g对比，放大倍数为4.4倍。

2.4 冲击分析

本文冲击分析取工作状态作为输入条件，对该电子模块结构进行冲击分析，分析结果如表5和图7所示。

表5 冲击分析结果

图7 y向冲击应力云图

x、y、z三个方向冲击应力最大值为72.6 MPa，方向为y方向，最大应力位置在销钉处，同样按照安全系数取1.5倍进行校核，仿真结果表明结构设计满足冲击试验要求。

2.5 加速度分析

对结构进行加速度分析，各向施加15g加速度进行过载有限元分析，分析结果如表6所示。

表6 加速度分析结果

x、y、z三个方向加速度分析最大变形值为64.8 μm，最大应力为21.7 MPa，同样按照安全系数取1.5倍进行校核，最大应力在安全范围内。过载时最大变形发生在z轴加速度试验中，变形量为64.8 μm远远小于影响导引头性能的0.5 mm量级，因此刚度满足要求。由此，仿真结果表明结构设计满足加速度试验要求。

2.6 有限元分析数据分析

通过以上对该导引头电子模块的正弦振动、随机振动、冲击、加速度有限元分析结果分析，各工况仿真计算的应力值均远小于材料的许用应力值，其中应力最大值发生在冲击工况中，且最大应力位置处于模块的销钉处，对模块整体的强度考核影响不大。因此仿真计算结果表明该模块结构设计远满足给定的力学环境条件，结构的强度有较大裕度，后续可考虑对该模块进行进一步的减重优化设计。

3 试验数据对比

为了对比计算机力学仿真结果与实测数据，验证有限元分析仿真模型建立和简化过程的合理性，可以通过对该电子模块样件施加相同的边界约束条件进行力学环境试验[3]。

基于以上力学仿真分析结果，冲击工况时构件所承受的最大应力值是该构件力学试验中最为恶劣的，且最大应力值处于可见位置，故对该构件进行瞬态冲击试验，提取试验过程最大应力值进行对比。

选用VP875型振动试验台进行力学试验，为取得电子模块的应力响应数据，将BF350-3AA80(23)N6-X型应变传感器通过双组份环氧树脂胶粘贴在冲击应力响应值最大点。以上力学仿真结果显示x,y,z三向结构的最大响应点均在中部左右分布的2个凹槽上，故将2个应变传感器分别粘贴在左右2个凹槽上，分别采集响应数据。按照试验流程，各向试验持续1 h，采集两点的最大瞬时应变数据并换算成应力值，结果如表7所示。

表7 冲击试验结果

将表7试验数据与仿真分析数据进行对比可知，x、y、z三向的应力最大值的误差分别为12.4%，15.1%，11.5%。三向误差均在16%以内，有一定的可信度，且x、y、z三向上冲击历程中最大应力时间与仿真值基本相同，故仿真结果与试验情况基本吻合，也表明有限元分析仿真模型的建立和简化合理、有效。试验结果也进一步印证了该电子模块能满足给定的力学环境。

4 结束语

本文针对弹载导引头复杂且严苛的力学环境对其中关键的电子模块进行了相关静力学和动力学的仿真分析，依托新型的计算机仿真软件Nastran为计算器进行模态分析、正弦振动、随机振动、冲击、加速度的仿真计算，提取处理结果进行分析并通过力学试验校核了结构的刚强度是满足设计需求的，验证了在复杂工作环境下结构的可靠性[5]。作为计算机结构设计中的重要一环，有限元分析计算可以有效地弥补传统力学试验成本高，周期长等固有的缺陷，辅助设计师了解设计结构的刚强度分布，在校核结构可靠性的同时也可以针对性的进行优化改进，大大缩短了设计周期，提高设计效率。