基于FPCA和PSOSVM回收塑料瓶分类

吴开兴，范亭亭，李丽宏，张 琳

(1.河北工程大学 信息与电气工程学院，河北 邯郸 056038；2.河北工程大学 煤矿综合信息化河北省工程实验室，河北 邯郸 056038)

0 引 言

现在国内外关于回收塑料瓶分类研究主要是颜色和化学成分方面[1]，而且数量较少，因此现在塑料瓶分类人工多于智能机械化。在智能处理回收塑料瓶的过程中，图像处理技术是其核心[2]，本文就针对回收塑料瓶颜色分类中的图像处理部分的算法进行研究。

颜色分类时，首先要选定合适的颜色模型，在结合了已有的塑料瓶颜色分类算法[3-5]和其它研究方向颜色分类[6]的颜色模型，选用了适合用于计算机对物体的颜色做定量分析和检测的HSI颜色模型。在处理图像数据时，因其维数度过高，需要进行降维处理，因此使用快速主成分分析(fast principal component analysis，FPCA)，相比较PCA能降低计算复杂度，使处理速度加快。借鉴于前人的工作经验，选用支持向量机(support vector machine，SVM)作为分类器。虽然SVM的分类方法已经较为成熟，在图像分类上也可以有效运用[7,8]，但其参数选取的不确定性，给分类造成了困难，因此采用粒子群算法(particle swarm optimization，PSO)来优化支持向量机参数[9]，因粒子群算法易陷入局部极值中，引入惯性权重和收敛因子，以获得最优参数，提高分类结果的稳定性，最终实现提高识别率的目的。因此，文中提出一种基于FPCA和PSOSVM的回收塑料瓶颜色分类算法，以达到进一步提高分类识别率的目的。

1 回收塑料瓶颜色分类算法内容

1.1 PCA降维处理和特征提取

文中处理的图像均为彩色图像，直接处理彩色图像得到样本矩阵，此时将样本用于计算，因其维数较高，最终造成计算量大且复杂度高的结果。所以，为减少计算量同时降低计算的复杂度，本文用FPCA法进行降维处理，获取少量且有效的特征向量用于分类识别。

主成分分析(PCA)的最终目的是为了获得样本协方差矩阵的本征值和本征向量。设样本X是n×d(n个d维样本特征向量)的矩阵，则对应的散布矩阵(协方差矩阵)S是d×d的方阵，因此所处理的样本维数较大时会增加计算复杂度。而本文所用的FPCA法降维处理的过程如下。

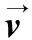
(1)

在式(1)两边同时左乘ZT，则有

(2)

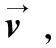
通过上述原理步骤得到协方差矩阵S，之后计算协方差矩阵的P个特征值λ1，λ2，…，λp，并按照大小进行排序。

根据式(3)计算第i个主成分分量的贡献率

(3)

通过贡献率计算样本的累计贡献率，当累计贡献率达到85%以上，就可以使用前n个主成分作为输入变量，以避免“维数灾难”引起的数据冗余。

1.2 SVM分类器模型

支持向量机因其高泛化性被广泛使用，文中也将采用径向基核函数的SVM作为分类器，其性能依赖于惩罚因子C和核函数参数σ[10]，选取合适的参数，其训练速度和训练精度均可提高。以下面SVM原理进行分类器模型构建。

假设(xi,yi),i=1,…,N是一组训练样本，其中xi∈Rd，d是输入空间的维数，yi∈{-1,1}。支持向量机的目的是将训练样本按照类别完全分开，最终使相同的样本处于所定义的超平面的同一侧。其约束条件为

yi(w·xi+b)>0,i=1,…,N

(4)

(5)

约束条件为

yi(w·xi+b)≥1,i=1,…,N

(6)

利用Lagrange优化方法可以将最优分离超平面问题转化为其对偶问题，即约束条件为

在此条件下求解下列函数的最大值

(7)

其中，α=(α1,…,αN)是Lagrange乘子，由上述方法得到的最优分类函数为

f(x)=sgn{(w·x)+b}

(8)

当数据线性不可分时，支持向量机引入一个松弛项ξi≥0和惩罚因子C，此时的目标函数变为

(9)

其约束条件为

yi[(w·xi)+b]-1+ξi≥0,i=1,…,N

(10)

令K(xi,xj)=φ(xi)·φ(xj)。

最终得到的分类函数为

(11)

K(x,y)为径向基核函数。

根据式(4)～式(11)构建本文所需的基本的径向基核函数的SVM模型。在此基础上进行参数的优化和分类识别。

1.3 PSO对SVM参数优化

文中为得到适合的惩罚因子C和核函数参数σ，采用粒子群算法进行参数优化。粒子群算法是一种采用“速度-位移”模式理论，并且时刻关注个体的踪迹进行迭代递推的算法，而且其具有较快的收敛速度[11]。

设群体数目为M，其个体i在p维空间的位置表示为xi=(xi1,xi2,xi3,…,xip)，其中i=1,2,3,…,M，速度表示为vi=(vi1,vi2,vi3,…,vip)。其中粒子的速度和位置会根据式(12)和式(13)不断的更新

vip=vip+c1rand1()(pbestip-xip)+
c2rand2()(gbestp-xip)

(12)

xip=xip+vip

(13)

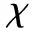
vip=ωvip+c1rand1()(pbestip-xip)+
c2rand2()(gbestp-xip)

(14)

(15)

经由上述的计算过程，通过反复的迭代运算，最终获得最优且适合的惩罚因子C和核函数参数σ。将结果用于SVM分类识别，以达到提高分类稳定性和准确率的目的。

1.4 回收塑料瓶颜色分类处理流程

对所使用的算法进行分析后，将算法进行结合对回收塑料瓶进行分类处理，整体的处理流程如图1所示的分类流程。

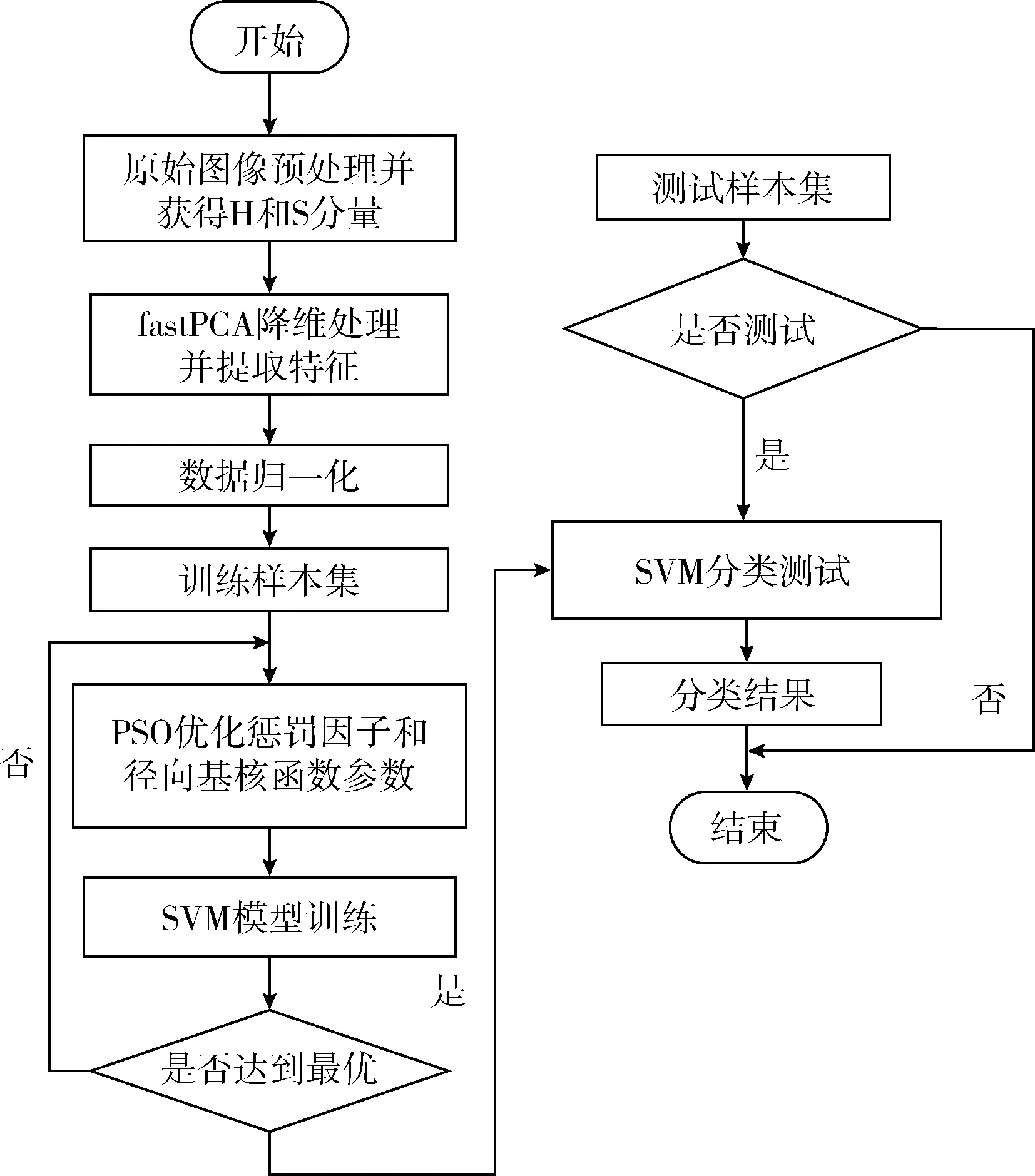
图1 FPCA和PSOSVM分类流程

整个处理流程的步骤介绍如下：

步骤1 获取回收塑料的图像，将图像转换到HSI模型下，对图像进行去噪、分割等预处理，并获得图像的H和S分量。

步骤2 对图像的H和S分量，使用FPCA进行降维处理，获得特征值，之后对数据进行归一化处理，将归一化获得的数据分为训练样本和测试样本。

步骤3 用训练样本作为数据进行PSO参数优化，用优化后的惩罚因子和径向基核函数参数进行SVM模型训练。

步骤4 对训练后的结果进行计算适应度是否达到最优，如果没有，则重复进行步骤3；如果达到最优，则进行下一步。

步骤5 使用测试样本，进行分类识别的测试，获得整体的识别率。

2 实验分析与结果

实验中对常见的蓝色、绿色、白色(文中提到的均为无色透明)塑料瓶进行了分类算法的研究。鉴于HSI颜色模型适合用于计算机对物体的颜色做定量分析和检测，而实验最终的目的是将塑料瓶按颜色进行分类，因此在HSI颜色模型的基础上对预处理后的图像进一步处理。

实验使用的是320*240的彩色图像，维数较高，因此在HSI模型下采用FPCA进行降维处理，得到其前6个主成分分量，如图2所示其累计贡献率可以达到85%以上，完全可以作为特征值使用。由图3可以显示出3个颜色的塑料瓶其特征量有较明显的区别，因此联合H和S分量获得有效特征值进行分类识别。

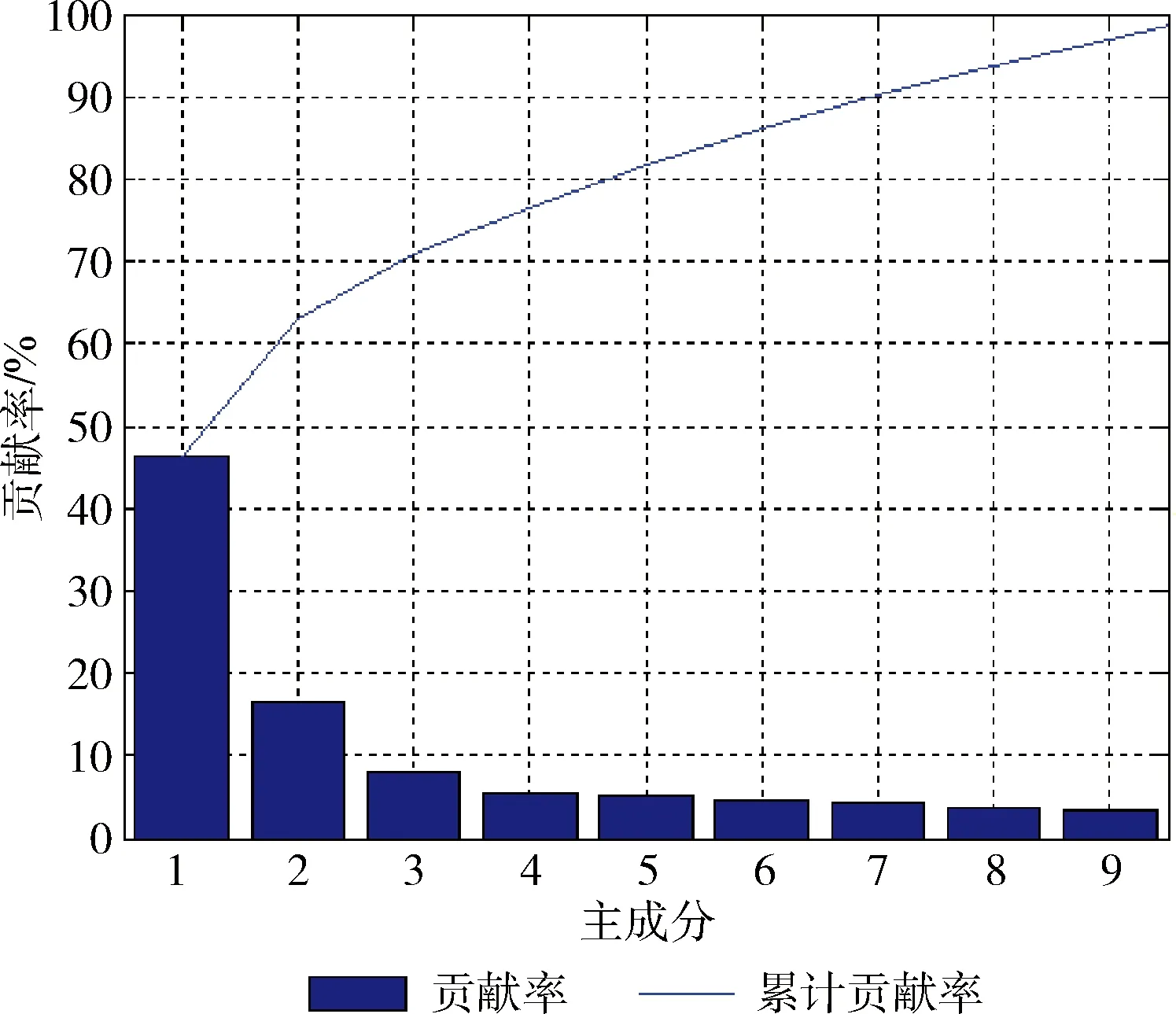
图2 主成分累计贡献率

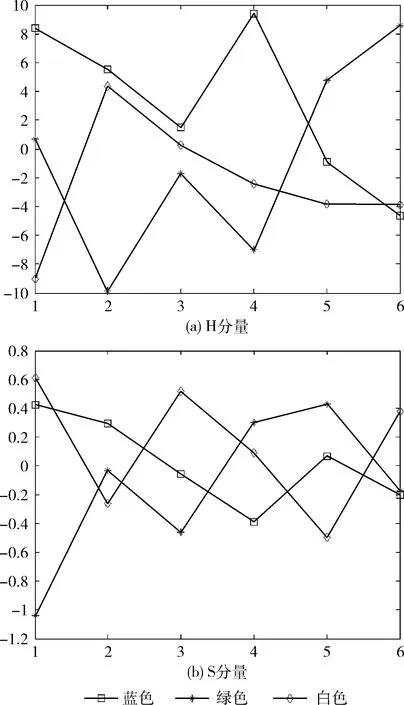
图3 HSI模型与快速PCA提取特征

实验数据为3种颜色，每种30个样本，对其进行上述的处理获得特征值后，数据分为训练集和测试集，使用SVM分类器进行分类识别。文中使用PSO对SVM的惩罚因子C和核函数参数σ进行参数寻优，图4可以看出初始时识别率并不是最优，随着迭代次数的增加，识别率有所提高，当迭代次数达到55左右时，整体的识别率达到93.4%，并且在之后随着迭代次数的增加趋于稳定。

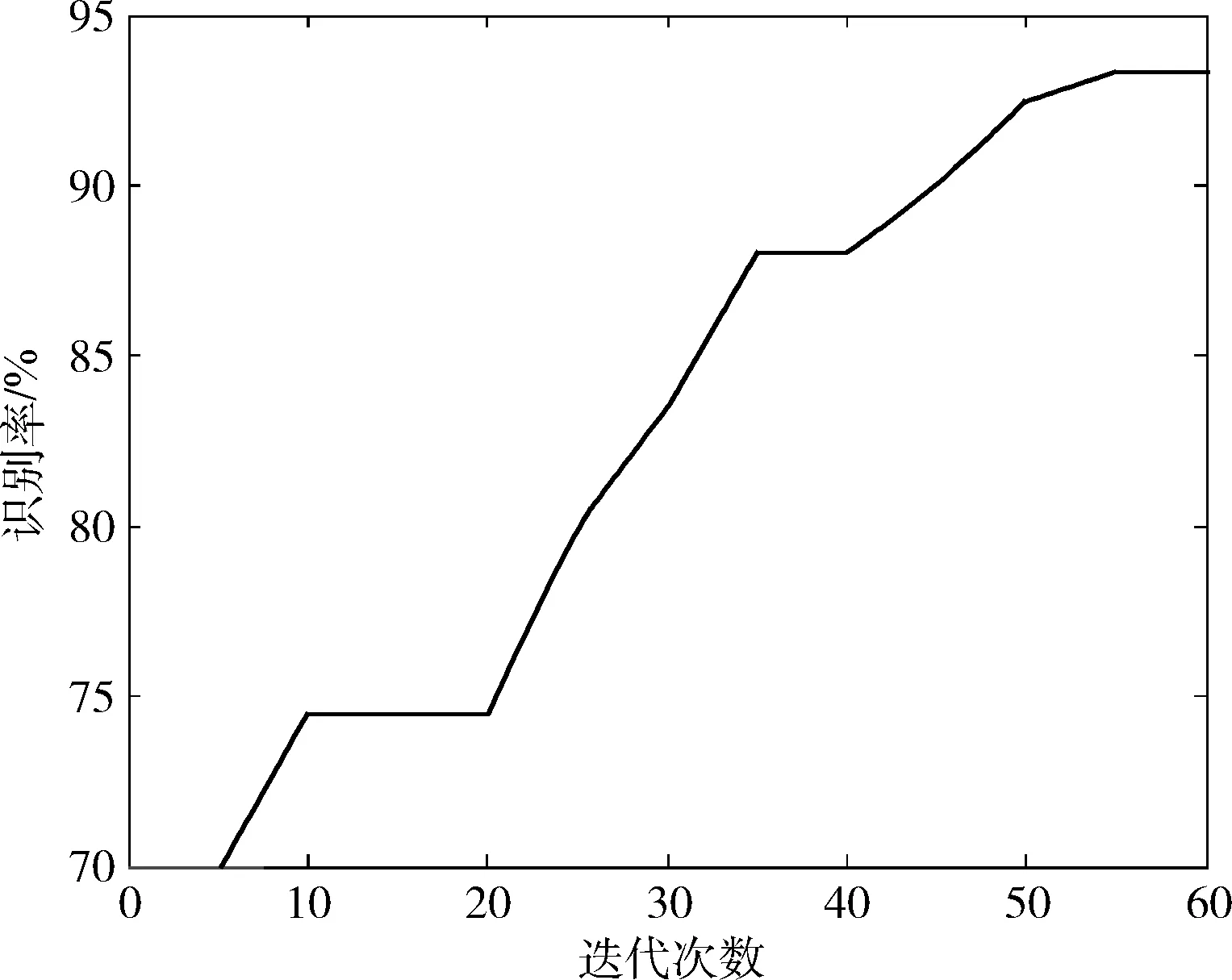
图4 迭代次数与识别率关系

实验使用测试集对文中所提算法进行测试，最终用PSO进行参数寻优和未进行参数寻优的实验结果见表1，结果显示文中所用算法整体的识别率有较显著提高。

表1 实验对比结果

3 结束语

文中提出了FPCA和PSOSVM算法用于回收塑料瓶颜色分类识别研究，其分类的识别率相对于未使用PSO进行参数寻优提高了5.8%左右，可以达到93.4%，比以前的研究也有所提高，因此，达到了提高分类识别率的目的，对于回收塑料瓶的分类研究具有一定的推动作用。快速主成分分析法有效的降低了样本的维数，减少了输入量，去除了原始数据的相关性，为分类识别提供了有效的特征值，降低了计算的复杂度。采用PSO优化SVM的参数，降低了参数选择的随机性，使实验结果更为稳定，下一步的实验可以用数据进一步验证此结果，以期进一步优化参数，提高分类识别率。