基于新加工硬化率方法的AZ80镁合金动态再结晶临界条件

王忠堂，霍 达，于晓林



基于新加工硬化率方法的AZ80镁合金动态再结晶临界条件

王忠堂1，霍 达2，于晓林1

(1. 沈阳理工大学 材料科学与工程学院，沈阳 110159；2. 东北财经大学 金融学院，大连 116025)

在变形温度为260~410 ℃、应变速率为0.001~10 s−1条件下，对AZ80镁合金进行热拉伸实验，测试AZ80镁合金的真应力−真应变曲线；依据Arrhenius本构方程形式，确定AZ80镁合金热变形过程的本构关系模型；提出一种新的加工硬化率方法，当加工硬化率函数对应变()求一阶导数后的函数取最小值时所对应的应变值，即为临界应变(c)。采用新的加工硬化率方法，确定AZ80镁合金在不同变形条件下动态再结晶的临界应变和临界应力；研究热变形工艺参数对临界应变和临界应力的影响规律；确定AZ80镁合金热变形过程中的临界应变、临界应力、稳定应变与参数的关系模型。模型计算结果与Sellars模型结果相吻合。

AZ80镁合金；加工硬化率；动态再结晶；临界条件

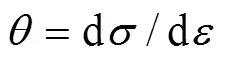
本文作者采用加工硬化率方法，研究AZ80镁合金发生动态再结晶临界条件，确定临界应变、临界应力和稳态应变与参数之间的计算模型。

1 应力−应变曲线

实验材料为轧制态AZ80镁合金板材，热拉伸变形实验温度分别为260、310、360、410 ℃；应变速率分别为0.001、0.01、0.1、1、10 s−1。不同变形条件下的真应力−真应变曲线，如图1所示。

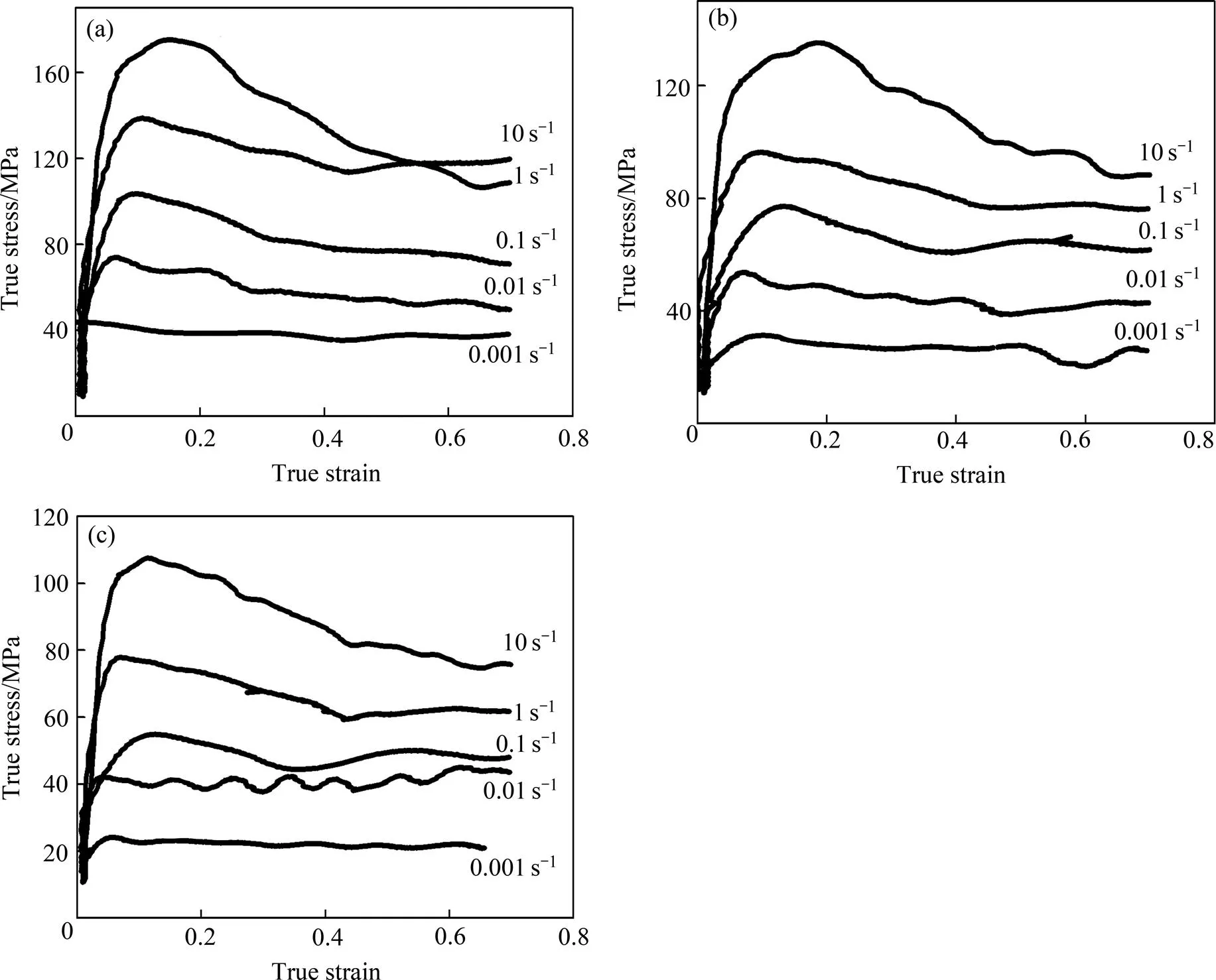
图1 AZ80镁合金的真应力−真应变 曲线

2 本构方程

SELLARS等[19]提出了一个双曲正弦的材料应力−应变本构方程，其中包括变形激活能、变形温度、应变速率等参量，见式(1)：

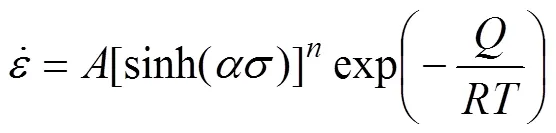
3 新加工硬化率方法定义

加工硬化率()的定义为材料发生塑性变形时发生加工硬化的程度，数学表达式为dd。图3所示为材料应力−应变曲线上不同区域所对应的加工硬化率变化规律。从图3可以看出，随着应变()值的增大，加工硬化率()值的变化过程可以分4个区域来分析，在Ⅰ区，加工硬化率值大于零，逐渐降低；在Ⅱ区，加工硬化率值小于零，且逐渐降低；在Ⅲ区，加工硬化率值小于零，且逐渐增大；在Ⅳ区，加工硬化率值趋于稳定在0值，且在0值附近波动，如图4所示。当应变值()小于稳定应变值(st)时，发生的动态再结晶为连续动态再结晶，而当应变值()大于稳定应变值(st)时，加工硬化率()值在0值附近上下波动，说明发生的动态再结晶是周期型动态再结晶。显然，在一次热拉伸变形过程中，加工硬化率()值的变化规律是从正值降低至负值，再从负值增大到0值的过程，第一次返回至0值时的应变值定义为稳态应变(st)，它所对应的应力−应变曲线上的应力值即为稳态应力(st)。稳态应变(st)是指材料完成动态再结晶时的应变值，如图3所示。

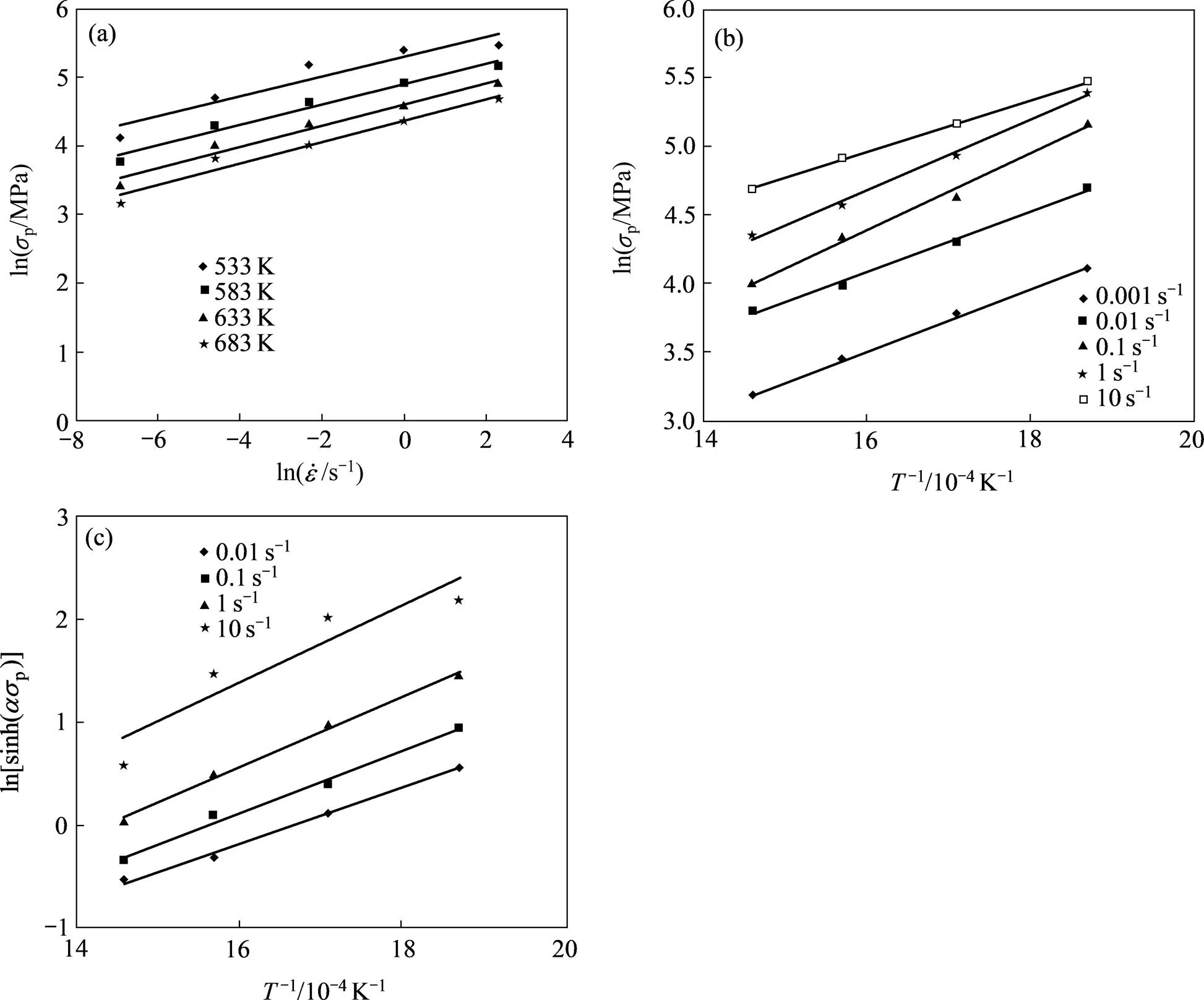
图2 峰值应力与应变速率和变形温度的关系

图3 不同阶段的加工硬化率

图4 加工硬化率的变化曲线

4 临界条件的确定

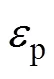
对图5(b)的应力−应变曲线进行非线性拟合，得到拟合方程，见式(3)：

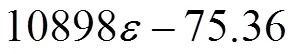
对式(3)求导数，得到：

对式(4)求导数，得到式(5)：

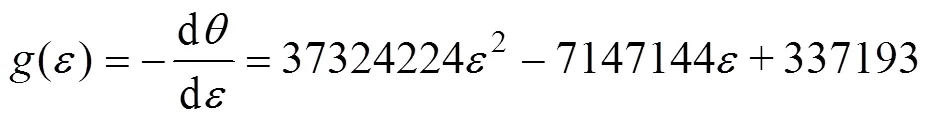
根据以上的分析方法，可以得到AZ80镁合金在不同条件下的动态再结晶时的临界应力和临界应变，如图6所示。从图6(a)和(b)可知，AZ80 镁合金的临界应变和临界应力随着变形温度的升高而降低，说明变形温度升高有利于发生动态再结晶。从图6(c)和(d)可以看出，应变速率对临界应变和临界应力都产生无益的影响，即随着应变速率的升高，临界条件也升高，这主要是因为当变形速率较高时没有充分的时间形成再结晶的晶核，从而使再结晶发生的比较慢，所以临界应变滞后。

图5 AZ80镁合金应力−应变曲线和加工硬化率(T=260 ℃，应变速率 1)

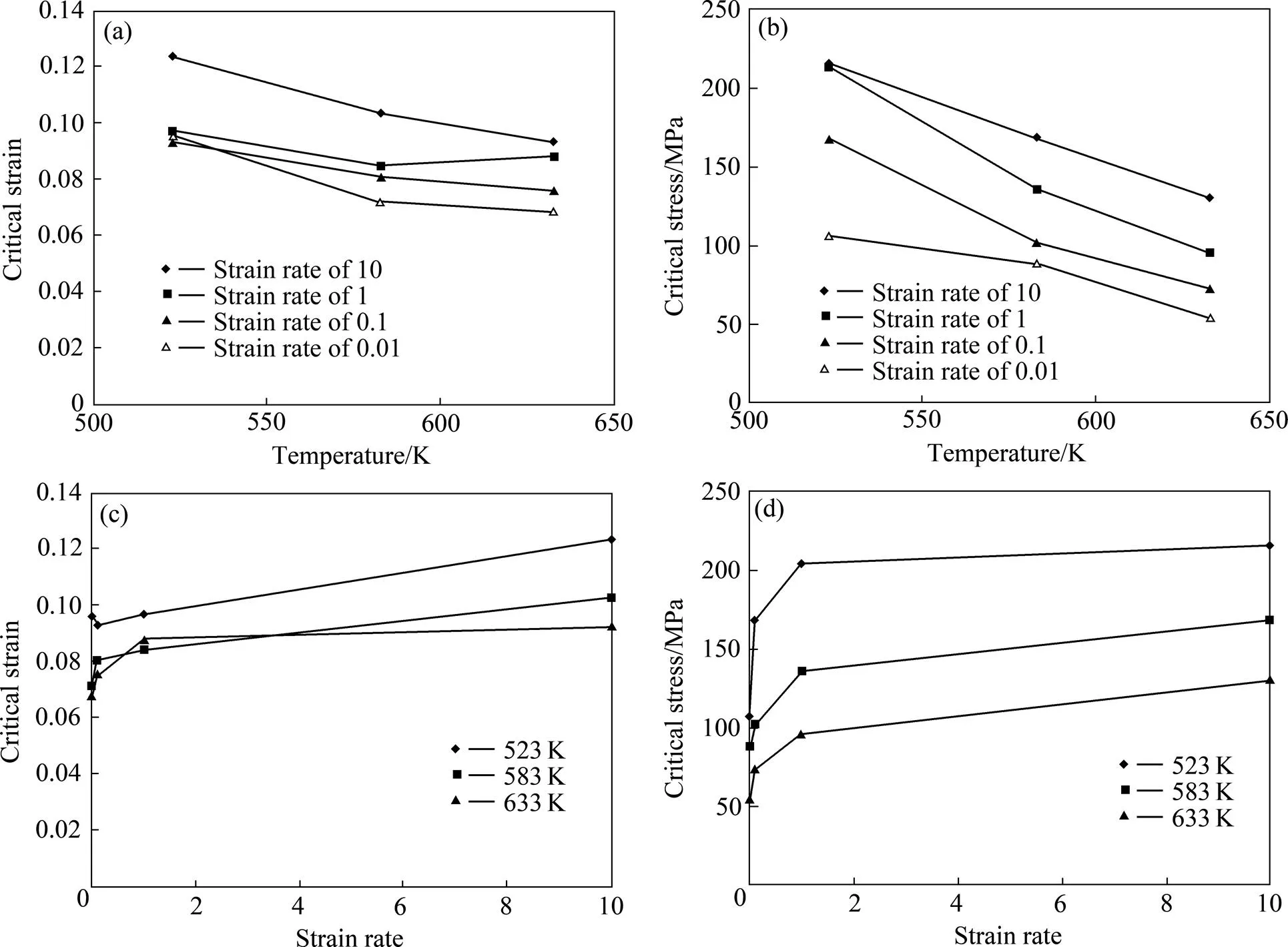
图6 AZ80镁合金动态再结晶的临界条件

5 动态再结晶时的稳态应变

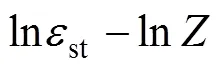
根据Kopp模型[20]可以得到：

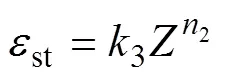
对式(7)求导数，得到式(8)：

根据图9的数据以及式(8)，可以得到2=0.1135，3=0.515。代入式(7)中，则得到动态再结晶完成时的稳态应变模型：

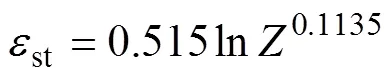
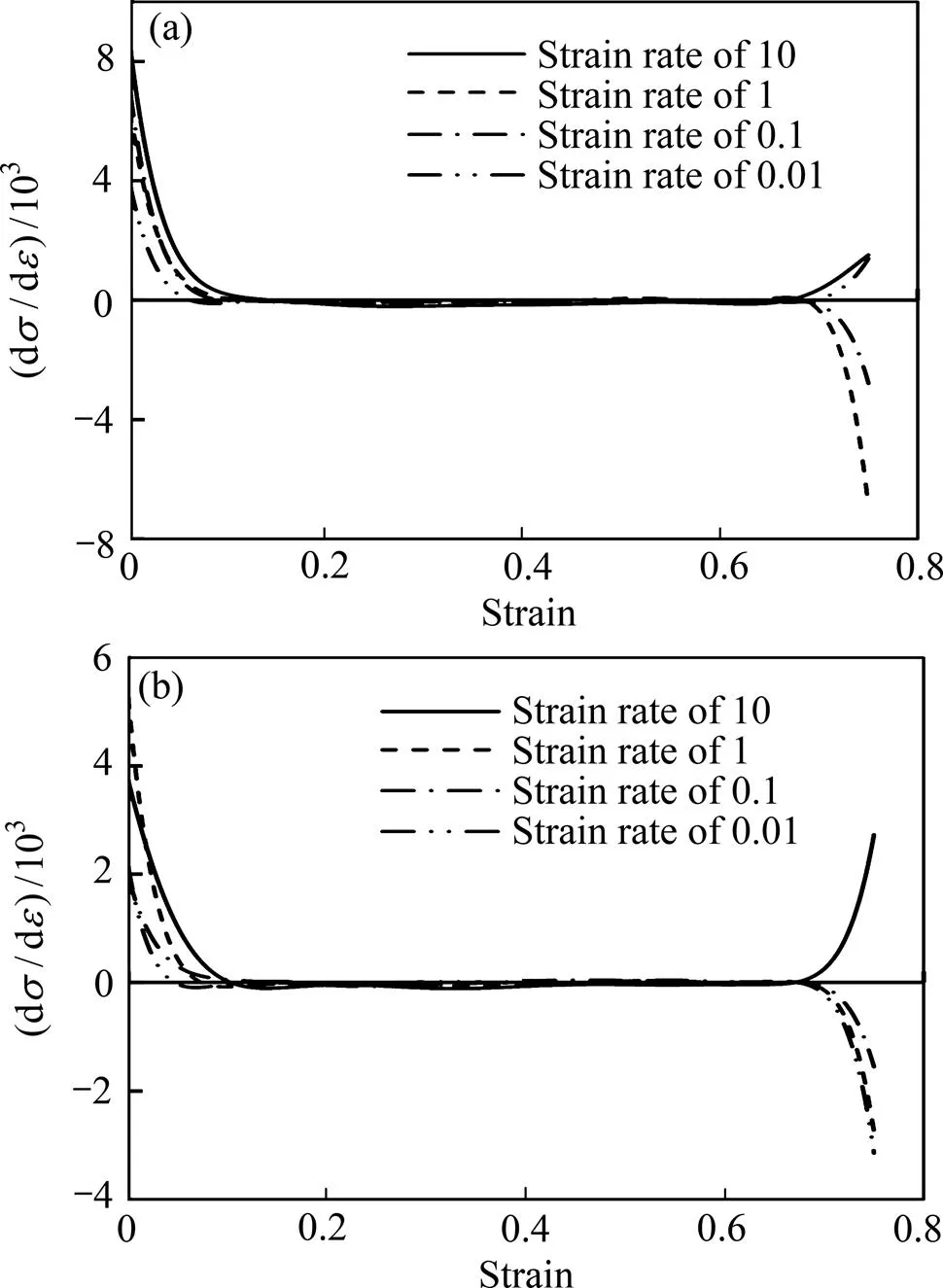
图8 不同温度下AZ80加工硬化率(θ)与应变关系曲线

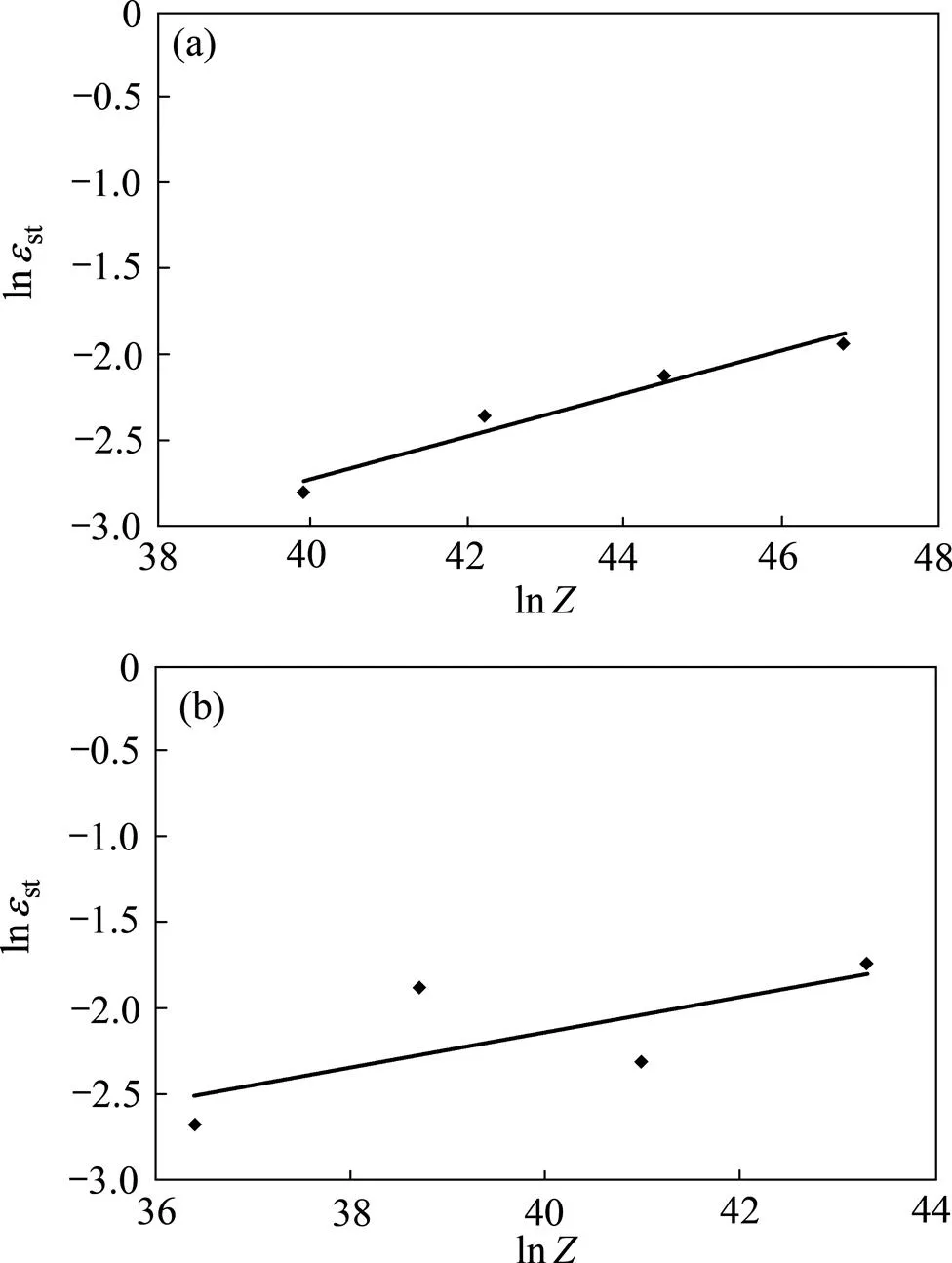
图9 不同温度下稳态应变与Z函数之间关系()

6 结论

1) 测试了AZ80镁合金的真实应力−应变曲线，依据Arrhenius本构方程形式，确定了AZ80镁合金变形激活能为140671J/mol，确定了AZ80镁合金热变形过程的本构关系模型。

2) 提出了一种新的加工硬化率方法，即当函数()=−d/d取最小值时所对应的应变值即为临界应变(c)，与临界应变(c)对应的就是临界应力(c)，简化了计算过程。

3) 采用加工硬化率方法，确定了不同变形条件下的临界应变和临界应力，随着变形温度的提高，临界应变和临界应力值降低；随着应变速率的增大，临界应变和临界应力值增大。

4) 确定了AZ80镁合金热变形过程中动态再结晶的临界条件和峰值条件与参数的关系模型，以及动态再结晶完成时的稳态应变(st)与参数的关系模型。

[1] 权国政, 赵 磊, 王 阳, 石 彧, 周 杰. 基于流动应力曲线的AZ80镁合金动态再结晶动力学表征[J]. 功能材料, 2011, 42(6): 1142−1146. QUAN Guo-zheng, ZHAO Lei, WANG Yang, SHI Yu, ZHOU Jie. A characterization for the dynamic recrystallization kinetics of AZ80 magnesium alloy based on flow curve[J]. Journal of Functional materials, 2011, 42(6): 1142−1146.

[2] 蔡 赟, 孙朝阳, 万 李, 阳代军, 周庆军, 苏泽兴. AZ80 镁合金动态再结晶软化行为研究[J]. 金属学报, 2016, 52(9): 1123−1132. CAI Yun, SUN Chao-yang, WAN Li, YANG Dai-jun, ZHOU Qing-jun, SU Ze-xing. Study on the dynamic recrystallization softening behavior of AZ80 magnesium alloy[J]. Acta Metallurgica Sinica, 2016, 52(9): 1123−1132.

[3] 王天一, 丁汉林, 刘育锋, 魏 峰, 张义伟,程广萍. Mg-1.0%Zn-1.5%Ca合金热压缩过程的显微组织及动态再结晶行为[J]. 中国有色金属学报, 2014, 24(10): 2474−2481. WANG Tian-yi, DING Han-lin, LIU Yu-feng, WEI Feng, ZHANG Yi-wei, CHENG Guang-ping. Microstructure and dynamic recrystallization behavior of Mg-1.0%Zn-1.5%Ca alloy during hot compression[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2474−2481.

[4] 金朝阳, 李克严, 吴欣桐, 严 凯. 镁合金高温流动特性与动态再结晶的关联机制[J]. 扬州大学学报(自然科学版), 2015, 18(3): 41−45. JIN Chao-yang, LI Ke-yan, WU Xin-tong, YAN Kai. Correlation between dynamic recrystallization and flow characteristics of high temperature magnesium alloys[J]. Journal of Yangzhou University(Natural Science Edition), 2015, 18(3): 41−45.

[5] 童小山, 彭 建, 石大伟, 潘复生, 彭 毅. ZM21及ZM61合金的热变形行为与动态再结晶临界条件的表征[J]. 中国有色金属学报, 2013, 23(8): 2069−2075. TONG Xiao-shan, PENG Jian, SHI Da-wei, PAN Fu-sheng, PENG Yi. Thermal compression behavior and characterization of dynamic recrystallization critical conditions for ZM21 and ZM61 magnesium alloys[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(8): 2069−2075.

[6] LIU Zhi-yi, HUANG Tian-tian, LIU Wen-juan, KANG Sukbong. Dislocation mechanism for dynamic recrystallization in twin-roll casting Mg–5.51Zn–0.49Zr magnesium alloy during hot compression at different strain rates[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(2): 378−389.

[7] 刘 筱, 朱必武, 李落星, 唐昌平. 挤压态AZ31镁合金热变形过程中的孪生和织构演变[J]. 中国有色金属学报, 2016, 26(2): 288−296. LIU Xiao, ZHU Bi-wu, LI Luo-xing, TANG Chang-ping. Twinning and texture evolution in extruded AZ31 magnesium alloy during hot deformation[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(2): 288−296.

[8] 娄 超, 张喜燕, 任 毅. 动态塑性变形下AZ31镁合金的孪生特征[J]. 中国有色金属学报, 2015, 25(10): 2642−2649. LOU Chao, ZHANG Xi-yan, REN Yi. Twinning characteristic of AZ31 magnesium alloy during dynamic plastic deformation[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(10): 2642−2649.

[9] SHAO Yi-chuan, TANG Tao, LI Da-yong, ZHOU Guo-wei, ZHANG Shao-rui, PENG Ying-hong. Polycrystal modeling of hot extrusion texture of AZ80 magnesium alloy[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(4): 1063−1072.

[10] WANG Zhi-qiang, CHAPUIS A, LIU Qing. Simulation of mechanical behavior of AZ31 magnesium alloy during twin-dominated large plastic deformation[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(11): 3595−3603.

[11] LI Ling, MURÁNSKY O, FLORES-JOHNSON E A, KABRA Saurabh, SHEN Lu-ming, PROUST Gwénaëlle. Effects of strain rate on the microstructure evolution and mechanical response of magnesium alloy AZ31[J]. Materials Science and Engineering A, 2017, 684: 37−46.

[12] CHEN Gao-jin, CHEN Liang, ZHAO Guo-qun, ZHANG Cun-sheng, CUI Wei-chao. Microstructure analysis of an Al-Zn-Mg alloy during porthole die extrusion based on modeling of constitutive equation and dynamic recrystallization[J]. Journal of Alloys and Compounds, 2017, 710: 80−91.

[13] SELLARS C M, WHITEMAN J A. Recrystallization and grain growth in hot rolling[J]. Metal Science, 1979, 13(3): 187−194.

[14] RYAN N D, KOCKS U F. A review of the stages of work hardening[J]. Solid State Phenomena, 1993, 35(36): 1−18.

[15] POLIAK E I, JONAS J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization[J]. Acta Materialia, 1996, 44(1): 127−136.

[16] NAJAFIZADEH A, JONAS J J. Predicting the critical stress for initiation of dynamic recrystallization[J]. ISIJ International, 2006, 46(11): 1679−1684.

[17] 欧阳德来, 鲁世强, 崔 霞. 应用加工硬化率研究TA15钛合金区变形的动态再结晶临界条件[J]. 航空材料学报, 2010, 30(2): 17−23. OUYANG De-lai, LU Shi-qiang, CUI Xia. Study on critical strains of dynamic recrystallization during β process in TA15 titanium alloy using working hardening rate[J]. Journal of Aeronautical Materials, 2010, 30(2): 17−23.

[18] 王忠堂, 邓永刚, 张士宏. 基于加工硬化率的高温合金IN690动态再结晶临界条件[J]. 材料热处理学报, 2014, 35(7): 193−197. WANG Zhong-tang, DENG Yong-gang, ZHANG Shi-hong. Critical conditions of dynamic recrystallization for super-alloy IN690 based on hardening rate[J]. Transactions of Materials and Heat Treatment, 2014, 35(7): 193−197.

[19] SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. ACTA Metallurgica, 1966, 14: 1136−1138.

[20] KARHAUSEN K, KOPP R. Model for intergrated process microstructure simulation in hot forming[J]. Steel Research, 1992, 63: 247−266.

Critical conditions of dynamic recrystallization of AZ80 magnesium alloy based on a new method of work hardening rate

WANG Zhong-tang1, HUO Da2, YU Xiao-lin1

(1. School of Materials Science and Engineering, Shenyang Ligong University, Shenyang 110159, China; 2. Dongbei University of Finance and Economics, Dalian 116025, China)

The curves of true stress−strain of AZ80 magnesium alloy are tested by thermal tensile method, which the ranges of temperature is from 260 to 410oC and strain rates is from 0.001 to 10 s−1. According to the Arrhenius equation，the constitutive model of AZ80 magnesium alloy at thermal deformation was determined. A new work hardening rate method was proposed. When the derivative of work hardening rate function takes minimum value, the corresponding strain is the critical strain(c). The work hardening rate method was used to determine the critical strain and critical stress of dynamic recrystallization under different deformation. The relation model of critical strain and critical stress and steady strain with Zener−Hollomn parameters () were established. Calculation results of the critical strain model are in good agreement with that of Sellar’s model.

AZ80 magnesium alloy; working hardening rate; dynamic recrystallization; critical condition

Project(51575366) supported by the National Natural Science Foundation of China; Project(LG201701) supported by the Education Department of Liaoning Province, China

2017-09-13;

2018-03-15

WANG Zhong-tang; Tel: +86-24-24680841, +86-13898896289; E-mail: ztwang@imr.ac.cn

国家自然科学基金资助项目(51575366)；辽宁省教育厅资助项目(LG201701)

2017-09-13；

2018-03-15

王忠堂，教授；电话：024-24680841，13898896289；E-mail: ztwang@imr.ac.cn

10.19476/j.ysxb.1004.0609.2018.10.03

1004-0609(2018)-10-1972-08

TG146.2

A

(编辑 龙怀中)