基于深度网络训练的铝热轧轧制力预报
魏立新,魏新宇,孙 浩,王 恒
基于深度网络训练的铝热轧轧制力预报
魏立新,魏新宇,孙 浩,王 恒
(燕山大学 工业计算机控制工程河北省重点实验室,秦皇岛 066004)
在铝热轧过程中,轧制力预报精度直接影响着成品的产量和质量。为了提高铝热连轧轧制力预报精度,提出一种基于深度学习方法的多层感知器(Multi-layer Perceptron,MLP)轧制力预报模型。模型利用MLP的函数逼近能力来回归轧制力。模型以小批量训练为基础,利用Batch Normalization方法稳定网络前向传播的输出分布,并使用Adam随机优化算法来完善梯度更新,以解决MLP模型难以训练的问题。仿真结果表明:模型使网络预测与实测数据的相对误差降低到3%以内,实现了轧制力的高精度预测。
铝热轧;轧制力预测;深度学习;多层神经网络;优化算法
在铝热轧轧制过程中,轧制力的预设定控制着轧制规程的设置。并且影响着成品的厚度与其力学性能,轧制力准确地预报可以减少带材头尾长度[1−3]。对于传统轧制力机理模型,由于复杂多变的轧制环境,以及各个参量之间的相互耦合关系,在机理模型中引入了许多假设,一旦测量产生误差或者假设不成立轧制力的预报会产生很大波动[4]。为了精确地预报轧制力,智能模型被广泛应用到轧制领域。
MAHMOODKHANI 等[5]将摩擦因数加入模型输入,使用有限元分析与神经网络相结合对轧制力进行了预报,实现了轧制力的实时预测。BYON等[6]建立了Shida和Misaka两种流变应力方程并结合有限元分析进行轧制力预测,得出了高温、中应变速率条件下的轧制力模型。CHEN 等[7]使用减法聚类将输入数据划分为多个子空间,并对每个子空间建立支持向量机SVM模型,最后利用主成分分析法合成每个子模型输出来预报轧制力,使得轧制力预报误差缩小到3.76%。杨景明等[8]改进遗传算法优化的BP神经网络对轧制力进行了预测,结果表明该方法实现了轧制力的高精度预测。赵文娇等[9]建立基于信度分配的小脑模型神经网络来预报轧制力,利用网络权值与样本激活地址来更新权值信度,以完善梯度更新时网络的误差分配,从而提高了了网络的收敛能力与预报精度。吕程等[10]全面考虑神经网络输入项并按主要影响因素对训练样本进行划分,使得网络预报的轧制力值更加准确。以上方法都优于传统的机理模型,提高了轧制力预报的精度,但无论基于BP、RBF或SVM建立的轧制力模型都属于浅层模型,其对复杂函数的表达能力与泛化能力都受到一定制约。而随着深度学习网络的发展,深度模型逐渐体现出其优点,深度模型具有更加优秀的函数表达能力与更强的特征学习能力[11]。因此,为了进一步提高轧制力的预报精度,使用深度模型预报轧制力并改进深度模型难以训练的问题。
本文作者使用多层BP神经网络作为轧制力预报的深度模型。并且为了增加网络的学习效率提升网络性能,使用Mini-batch梯度下降作为模型的基础学习方式来加快网络训练速度并且为网络的训练提供随机性;使用Batch Normalization优化网络前向传播,稳定每层网络的输入分布;使用Adam随机优化算法优化网络反向传播,在梯度更新中为不同参数提供自适应性学习率,完善梯度更新。
1 深度网络模型
1.1 多层BP神经网络
常规BP神经网络由输入层、一个或多个隐藏层以及输出层组成,其结构如图1所示。由于神经网络对复杂函数的表达能力随着网络层数的增加而增 强[12],所以对于层BP神经网络(≥3),当其训练得当时,其效果可超越常规BP网络与SVM等为2的智能模型。但是随着网络层数的增加同时,也导致了网络训练难度上升的问题,其中主要包括:随着网络层数增加导致的训练时间过长;网络在训练过程中发生的协变量转变;非凸优化导致网络收敛到局部最小或鞍点以及梯度弥散导致的网络退化。本研究将通过深度学习算法来解决上述问题。
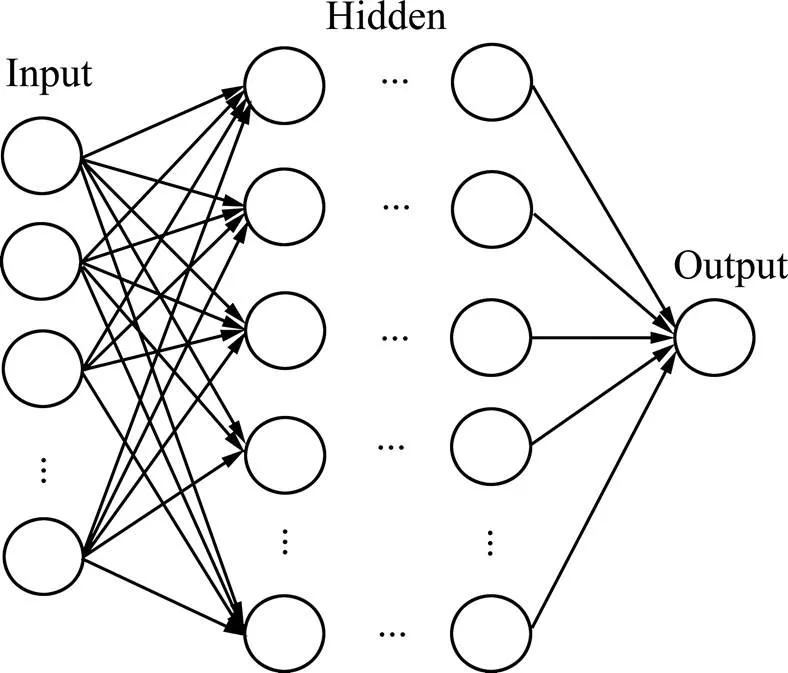
图1 多层神经网络结构
1.2 Mini-batch梯度下降
对于传统梯度下降算法每次迭代都需要在整个样本集上进行计算,当样本量较大时,会严重消耗计算资源,造成收敛速度过慢。同时由于在每次计算中都考虑所有的训练数据,丧失了训练的随机性,容易造成模型过拟合。随机梯度下降对传统梯度下降有了极大的提升,但是由于过度自由的训练(单个样本)导致损失函数在训练过程中产生较大波动。且训练中每次迭代只考虑单个样本,造成模型的整体性缺失以至于无法收敛。Mini-batch梯度下降可看做传统梯度下降与随机梯度下降的中和,该方法既保留了随机梯度下降在速度上的优势,又使模型的训练具有整体性。
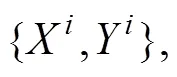
采用Mini-batch梯度下降作为网络的基础学习方式。MLP模型训练时间随着网络层数与样本数量的增加而增加。为满足模型对多层网络与大样本的需求,在模型训练中使用Mini-batch来减少训练时间,加快模型收敛速度。同时也为Batch Normalization与Adam随机优化算法的使用提供基础。
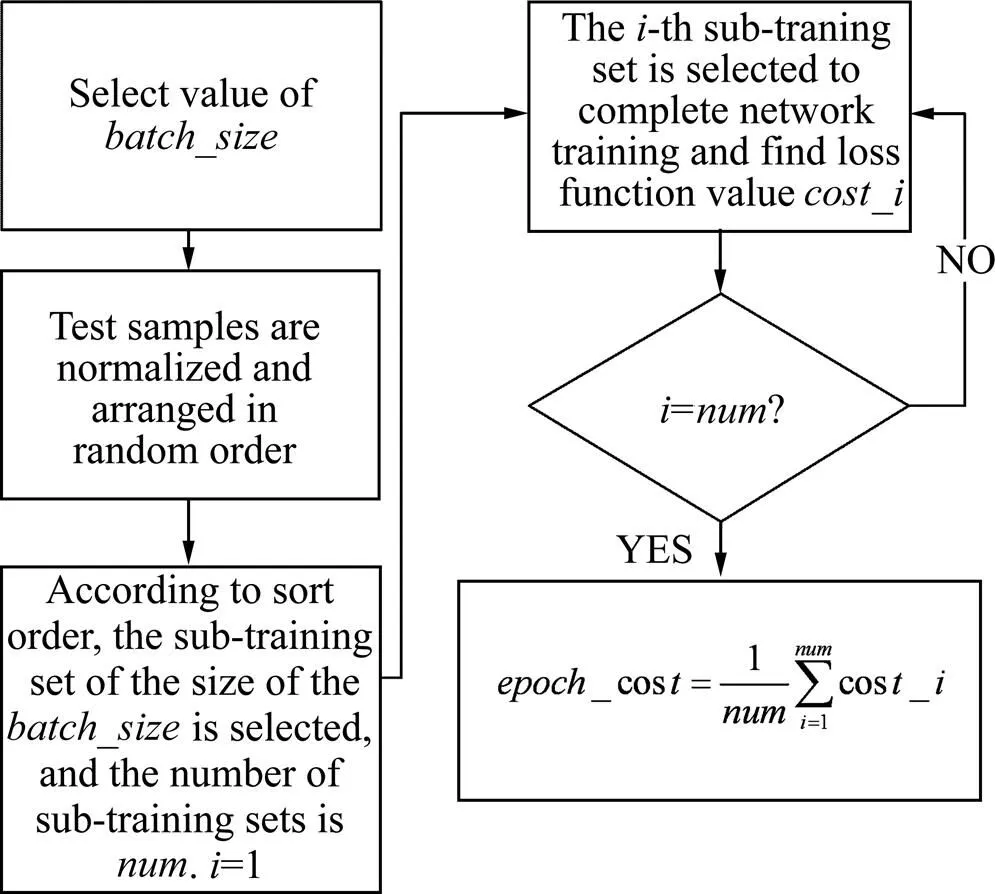
图2 单轮损失函数计算流程图
1.3 Batch Normalization
在训练单隐层网络时,对训练数据与测试数据进行预处理,使两者属于相同分布,可以加快网络的训练速度与提高模型精度。而对于多隐层网络,网络中的每一层都可以看作一个单隐层的子网络。每一层的输入都受到此层前所有层的影响。参数的微小变化会随着网络的深度而增大,从而影响子层网络输入,造成在训练过程中该层输入分布不断改变,导致covariate shift的出现。后层网络将不得不去适应新分布的产生,从而导致网络精度的下降与训练速度的降低。
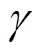
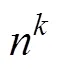
1) 对于任意层子网络,线性表达式为:
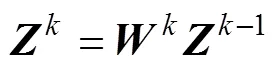
2) 使用式(2)和(3)求出层子网络每个神经元输出的均值与方差
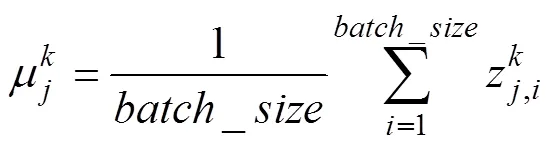
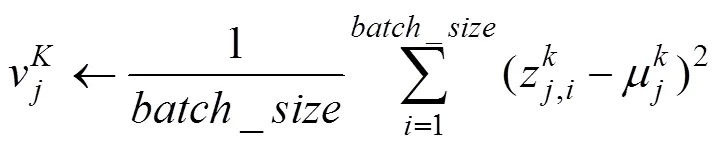
3) 利用指数移动平均法估计层子网络总体均值与方差,表达式如下:
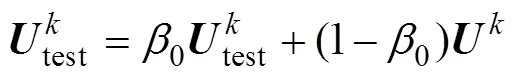
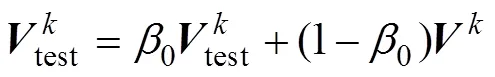
4) 规范化层子网络,具体如下:
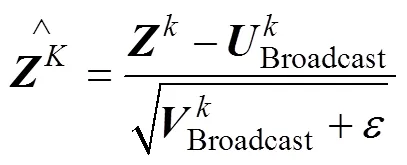
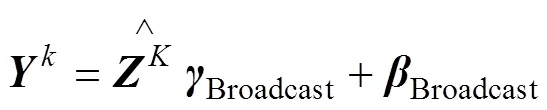
Batch Normalization在模型中的应用不仅可以极大地加快网络的训练速度,同时减少前层网络参数改变对后层网络的影响,使模型中每层网络的学习相对独立,使网络的训练更有效率。并且与Mini-batch相结合,利用子样本的均值与方差取代总体方差,为模型引入噪音,使得模型具有更好的泛化能力。
1.4 Adam随机优化算法
对于多隐层神经网络,随着网络层数的增加局部极小点与鞍点的数目都成倍的增长。使得网络的训练更容易陷入局部最小点甚至鞍点。传统的梯度下降算法由于对初始点极为敏感与使用固定的学习率,不适于在多隐层神经网络中使用。为获得更好的梯度更新效果,可使用BP算法的改进方法,主要包括:动量方法Momentum、采用自适应学习率的AdaGrad方 法[14]等。采用结合动量方法与自适应学习率的Adam随机优化算法来更新网络梯度。
Adam算法[15]是由 KINGMA 和多伦多大学的BA所提出的, 该方法基于适应性矩估计,能够完成随机目标函数的梯度优化。算法利用指数移动平均方法估计网络梯度的一阶矩(均值)与二阶矩(方差),用来为不同的参数提供独立的自适应学习率。并且使梯度的更新具有动量效果。更适用于多隐层神经网络这种非凸优化。
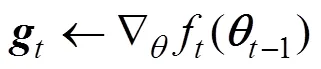
Step3:使用指数移动平均估计梯度期望与平方梯度期望,表达式如下:
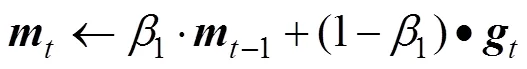
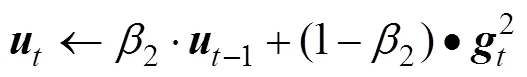
Step4:引入偏差修正,使用(11)与(12)求出两个期望的无偏估计。
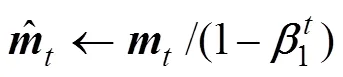
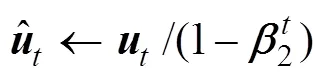
Step5:按照式(13)完成梯度更新,返回Step2。
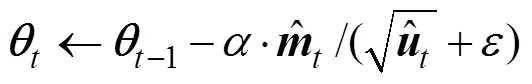
同时使用Adam优化算法与Mini-batch梯度下降来对模型进行训练。 Adam算法目标是降低随机目标函数的期望值,而目标函数的随机性主要来源于随机的子样本,Mini-batch在每个历元中都随机打乱样本顺序为模型训练提供随机的子样本,满足Adam对随机性的要求。在Adam算法中利用梯度估计均值与估计方差为不同参数提供更好的自适应学习率,使梯度得到规范化,完善梯度更新。并且Mini-batch单次迭代使用大小为Mini-batch的子样本,迭代速度较快。从而两者的结合提高了模型收敛精度与收敛性能。
2 轧制力预测
2.1 轧制力预测模型
该预测方法使用多隐层神经网络作为深度模型对轧制力进行预报。并以Mini-batch梯度下降为基础,分别使用Batch Normalization于Adam随机优化算法优化网络的正向传播与反向传播。
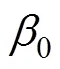
为防止模型训练可能会出现的梯度弥散,在隐藏层中未使用sigmoid等饱和非线性函数,而是使用激活函数Relu,函数图像如图3所示。
Relu激活函数克服了许多传统激活函数的缺陷。传统激活函数sigmoid函数结构复杂,使网络在梯度计算时计算量变大,且由于其具有饱和非线性特性,在饱和区处梯度大小接近于0,造成了网络的梯度弥散。而Relu函数的结构简单,不仅简化了网络的反向传播,也抑制了梯度弥散的产生。更为重要的是由于Relu激活函数的单侧抑制,使得网络自己引入了稀疏特性,从而缩小纯监督学习神经网络与包含无监督预训练神经网络的性能差距[17]。使得网络在不经过无监督学习的情况下,仍能的到理想的预测结果。
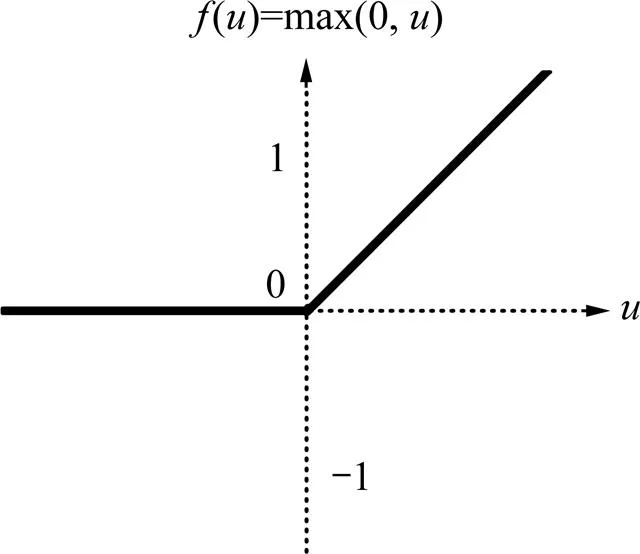
图3 Relu激活函数
网络结构简图如图4所示。
2.2 样本数据的选择
对于传统SIMS热连轧轧制力数学模型其计算公式为
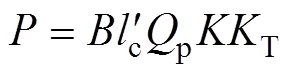
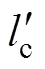
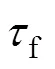
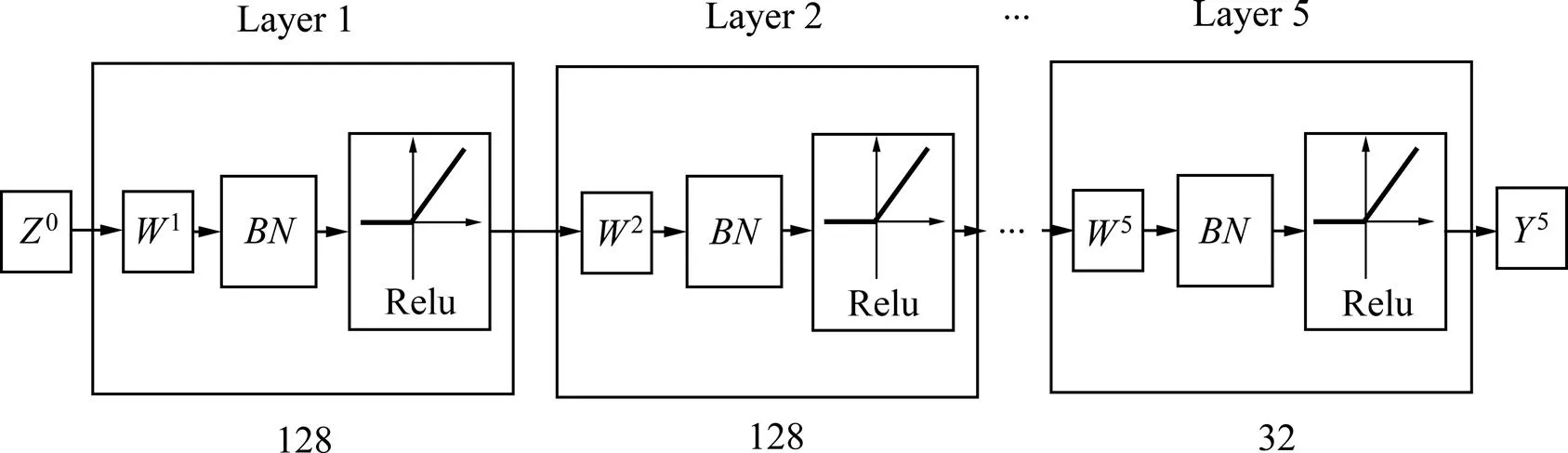
图4 网络结构简图
2.3 仿真与分析
利用建立起来的深度神经网络模型进行轧制力预测仿真。预测模型的输入向量为(,,1,2,,f,b,),损失函数为
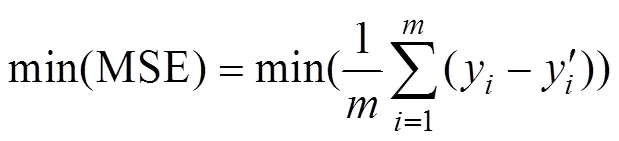
利用河南某厂铝热连轧生产线的在线数据,选取其中的第2机架中的数据9000条对模型进行训练。在训练前,对所有样本数据进行规范化处理。利用训练好的网络模型,对不在训练集中的600多条轧制力数据进行预测,其预测结果如图5所示。
从图5中可以看出,该模型具有较高的预测精度,其预测的相对误差可以控制在3%以内,可以满足生产要求。
表1所列为该模型与其他模型在限定时间500 s下,建模时间,平均相对误差,平均绝对误差与决定系数之间的比较,其中遗传算法优化的BP网络学习率取0.9,隐藏层神经元数为128。多层神经网络MLP未使用深度学习相关方法,但结构不变。为了消除随机性对模型影响,使用 10次预测结果的平均值来作对比。
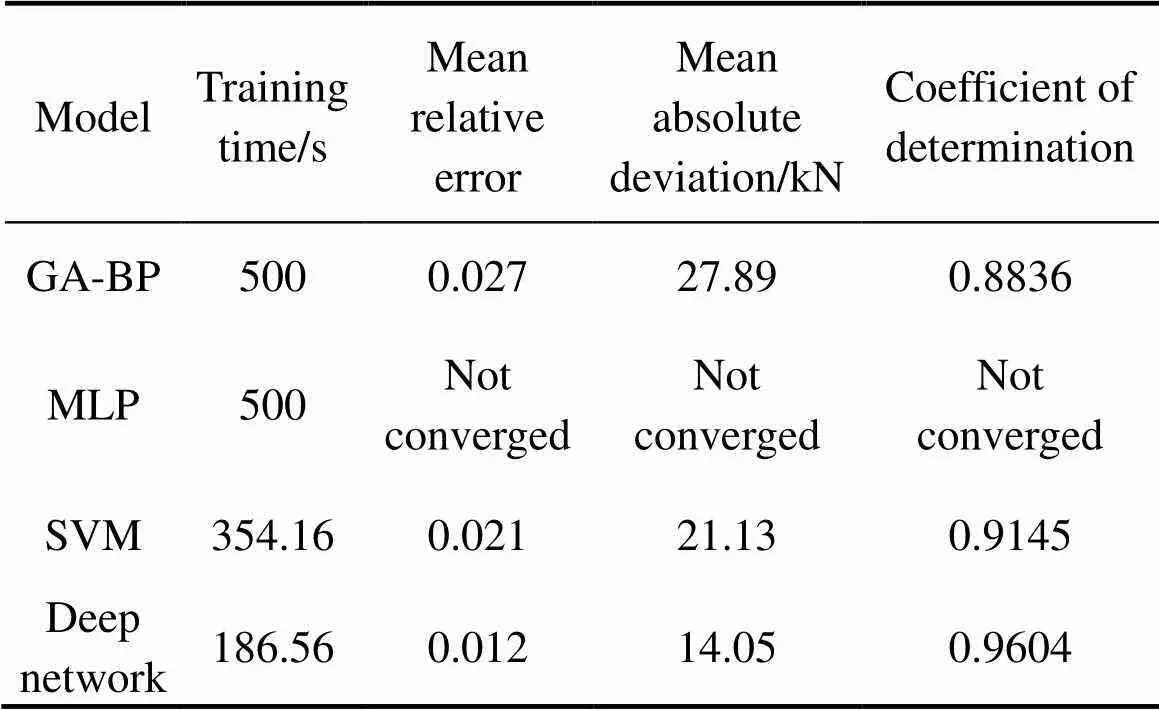
表1 模型预测结果对比
由表1可以看出,多层神经网络在无相关优化算法的情况下无法完成收敛。深度网络模型的建模时间为186.56s,其预测速度与预测精度上皆高于其他智能模型。
3 结论
1) 使用多隐层神经网络建立轧制力预测模型。并为了解决多隐层网络存在的固有缺陷,使用深度学习相关方法优化网络,其中主要使用了Batch Normalization加快网络的训练速度,解决因网络层数增多引起的训练时间过长的问题,Adam随机优化算法的应用避免了网络在训练过程中陷入局部最优点以及鞍点,提高了网络向最优解收敛的能力。
2) 该方法下轧制力预测的平均相对误差为1.2%。相对于优化算法优化的BP网络,其预报平均相对误差降低了1.5%。并且使得网络的训练时间降低到186.56 s,相对于SVM模型其收敛速度提升了接近1/2。综上所述,该方法在实践中具有很大的应用潜能。
[1] LIU X, LIU X H, SONG M, SUN X K, LIU L Z. Theoretical analysis of minimum metal foil thickness achievable by asymmetric rolling with fixed identical roll diameters[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(2): 501−507.
[2] ZUO Y B, FU X, CUI J Z, TANG X Y, MAO L, LI L, ZHU Qing-feng. Shear deformation and plate shape control of hot-rolled aluminium alloy thick plate prepared by asymmetric rolling process[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(7): 2220−2225.
[3] 燕 猛, 黄华贵, 张彩云, 杜凤山, 张尚斌. 板坯头/尾部平面形状对铝合金厚板粗轧头尾切除量的影响[J]. 中国有色金属学报, 2017, 27(6): 1102−1108. YAN Meng, HUANG Hua-gui, ZHANG Cai-yun,DU Feng-shan, ZHANG Shang-bin. Effect of the shape of the head/tail of the slab on the head and tail cutting of aluminum alloy thick plate[J]. Chinese Journal of Nonferrous Metals, 2017, 27(6): 1102−1108.
[4] OROWAN E. The calculation of roll pressure in hot and cold flat rolling[J]. Proceedings of the Institution of Mechanical Engineers, 1943, 150(1): 140−167.
[5] MAHMOODKHANI Y, WELLS M A, SONG G. Prediction of roll force in skin pass rolling using numerical and artificial neural network methods[J]. Ironmaking & Steelmaking, 2016, 44(4): 281−286.
[6] BYON S M, NA D H, LEE Y S. Flow stress equation in range of intermediate strain rates and high temperatures to predict roll force in four-pass continuous rod rolling[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(3): 742−748.
[7] CHEN Z M, LUO Z L. Rolling force prediction based on multiple support vector machines[C]// WATADA J. Proceedings of the 32nd Chinese Control Conference. New York: IEEE Press, 2013: 3306−3309.
[8] 杨景明, 顾佳琪, 闫晓莹, 车海军. 基于改进遗传算法优化BP网络的轧制力预测研究[J]. 矿冶工程, 2015, 35(1): 111−115.YANG Jing-ming, GU Jia-qi, YAN Xiao-ying, CHE Hai-jun. Prediction of rolling force based on improved genetic algorithm for optimizing BP neural network[J]. Mining and Metallurgical Engineering, 2015, 35(1): 111−115.
[9] 赵文姣, 闫洪伟, 杨 枕, 温玉莲 , 孙祖乾. 基于CA-CAMC网络的轧制力自学习预报模型[J]. 冶金自动化, 2016, 40(2): 7−10. ZHAO Wen-biao, YAN Hon-wei, YANG Zhen, WEN Yu-lian, SUN Zu-qian. Rolling force self-learning prediction model based on CA-CAMC network [J]. Metallurgical Industry Automation, 2016, 40(2): 7−10.
[10] 吕 程, 王国栋, 刘相华, 姜正义, 朱洪涛, 袁建光, 解 旗. 基于神经网络的热连轧精轧机组轧制力高精度预报[J]. 钢铁, 1998, 33(3): 33−35. LÜ Cheng, WANG Guo-dong, LIU Xiang-hua, JIANG Zheng-yi, ZHU Hong-tao, YUAN Jian-guang, XIE Qi. High-precision prediction of rolling force in hot rolling finishing mill based on neural network[J]. Iron and Steel, 1998, 33(3): 33−35.
[11] HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527−1554
[12] 毛勇华, 桂小林, 李 前, 贺兴时. 深度学习应用技术研究[J]. 计算机应用研究, 2016, 33(11): 3201−3205. MAO Yong-hua, GUI Xiao-lin, LI Qian, HE Xing-shi. Research on deep learning application technology[J]. Journal of Computer Applications, 2016, 33(11): 3201−3205.
[13] IOFFE S, SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]// BACH F. Proceedings of the 32nd International Conference on Machine Learning. Massachusetts: MIT Press, 2015: 448−456.
[14] DUCHI J, HAZAN E, SINGER Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. Journal of Machine Learning Research, 2011, 12(7): 257−269.
[15] KINGMA D P, BA J L. Adam: A method for stochastic optimization[C]// KINGSBURY B. Proceedings of the the 3rd International conference on learning representations. San Diego: arXiv, 2015: 1412−6980.
[16] GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[J]. Journal of Machine Learning Research, 2010, 9: 249−256.
[17] GLOROT X, BORDES A, BENGIO Y. Deep sparse rectifier neural networks[C]// BACH F. Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Massachusetts: MIT Press, 2011: 315−323.
[18] 杨景明, 孙晓娜, 车海军, 刘 畅. 基于蚁群算法的神经网络冷连轧机轧制力预报[J]. 钢铁, 2009, 44(3): 52−55. YANG Jing-ming, SUN Xia-ona, CHE Hai-jun, LIU Chang. Prediction of rolling force in neural network cold rolling mill based on ant colony algorithm[J]. Iron and Steel, 2009, 44(3): 52−55.
Prediction of aluminum hot rolling force based on deep network
WEI Li-xin, WEI Xin-yu, SUN Hao, WANG Heng
(Key Lab of Industrial Computer Control Engineering Department of Yanshan University, Qinhuangdao 066004, China)
In the aluminum hot rolling, the prediction accuracy of the rolling force directly affects the output and quality of the finished product. In view of the inherent defects of traditional rolling force model, a MLP rolling force prediction model based on deep learning method was proposed. The model uses MLP’s function approximation ability to regress the rolling force. Based on the Mini-batch training, the model uses Batch Normalization method to stabilize the output distribution of the network forward propagation, and uses the Adam stochastic optimization algorithm to improve the gradient updating so as to solve the difficult training problem of the MLP model. The simulation results show that the model can reduce the relative error between the network prediction and the measured data to less than 3%. Compared with the traditional mathematical model, this method realizes the high precision prediction of the rolling force, and realizes a high-precision prediction of rolling force.
aluminum hot rolling; rolling force prediction; deep learning; multilayer neural network; optimization algori
Project(F2016203249) supported by the Natural Science Foundation of Hebei Province, China
2018-03-27;
2018-07-23
WEI Li-xin; Tel: +86-335-8387556; E-mail: wlx2000@ysu.edu.cn
河北省自然科学基金资助项目(F2016203249)
2018-03-27;
2018-07-23
魏立新,教授,博士;电话:0335-8387556;E-mail: wlx2000@ysu.edu.cn
10.19476/j.ysxb.1004.0609.2018.10.14
1004-0609(2018)-10-2070-07
TG339
A
(编辑 王 超)

