一种图像特征点匹配算法——Haar-Gaussian&NICD算法

北京信息科技大学 自动化学院，北京 100192

一、引言

随着社会的发展，在图像识别领域小波变换是傅里叶变换之后的另外一个比较有力的工具。原则上讲，传统意义上使用傅里叶分析的地方，都可以用小波分析来替代[1]。就多分辨率分析而言，小波变换的出现使得图像处理领域又提供了一种新思路，小波框架的产生使得处理数字信号更加的精准。1989年，为了研究图像的纹理特征Mallat引入了小波的概念，为后续的基于小波纹理分析的方法提供了扎实的理论基础。小波变换是在不同尺度上研究分析图像文理细节的一种工具，为更精准的进行图像纹理分类和分析提供了新的思路，在纹理分析中有广阔的发展空间[2]。

图像的局部特征提取——特征点提取，在实现图像合成、图像校正、识别分类、图像匹配等图像领域常见问题中是及其重要的一个环节，关于如何在一幅图像中精准的定位其稳定的特征点用于后续的相关工作，国内外大量的相关学者和专家都做了深入的研究工作。

其中有一种较为广为人知的图像特征点提取算法称为Harris角点检测算法[3]。虽然这种算法对图像平移、旋转、和噪声具有较强的鲁棒性，但是当图像遭遇到尺幅变换之后其效果会很糟糕，因此从一定程度上来讲它的使用会受到限制。随着图像技术的发展，越来越多的基于强特征点提取匹配的算法被提出，其中包括SIFT算法[4]、Harris-Laplacian算法[5]等。

本文主要讨论一种特征点检测子算法的实现，并与规范化强对比度描述子（Normalized intensity contrast descriptor，NICD）相结合，目的是设计实现一种适用于一定程度的尺度变换、旋转情况下快速提取独特性强特征点的特征检测算法。本文的主要思路是将原始图片进行3层哈尔小波变换，得到不同尺度和不同方向上的图像信息，利用高斯函数进行不同尺度的高斯滤波进而产生哈尔小波高斯金字塔塔林，再利用高斯拉普拉斯函数计算提取相对最稳定的图像强度特性特征点，在通过计算来修正特征点，最后引进NICD描述子对所提特征点进行描述。

二、检测子的设计

1、小波理论

小波理论中重要的部分是多分辨率分析即多尺度分析，这也是与我们人的眼睛观察物体时的机理高度相似的。因为我们是对图像进行操作所以在这里我们重点讨论二维小波变换。在二维情况下，首先定义一个尺度基函数和平移基函数：

其中，上标i—沿列、行、对角方向。

于是，大小为M×N的图像f(x,y)的离散小波变换是：

其中，j0是其中一个开始的任意尺度，Wφ(j0,m,n)系数为定义f(x,y)在尺度j0处的近似，WΨ i(j,m,n)系数对尺度j≥j0增添了水平、铅垂和斜对角方向的细节。

因为有j=0,1,2,…,J-1和m=n=0,1,2,…,2j-1，所以通常情况下令j0=0，并且选择N=M=2J。图1展示了这一过程，在二维情况下我们得到3组细节系数——水平系数、铅垂系数和对角线细节系数。

本文中主要应用哈尔小波变换，因为它的基波是最古老的且最简单的正交小波，所以哈尔小波变换是其中最重要的一个环节。哈尔变换可以用如下矩阵形式表示：

其中，F—一个N×N的图像矩阵；

H—一个N×N的哈尔变换矩阵；

T—一个N×N的变换结果。

因为H的非对特性，所以在这里转置是必须要有的，其包含哈尔基函数hk(z)。它们定义在连续闭区间z∈[0,1]，k=0,1,2,…,N-1 上，其中N=2n。

为了得到矩阵H，本文在这里定义整数k，即k=2p+q-1，其中0≤p≤n-1。当p=0时，q=0或1；当p≠0时，1≤q≤2p。

因此，哈尔基函数为：

N×N哈尔变换矩阵的第i行包含了元素hi(z)，其中：。

2、Haar-Guassian金字塔塔林

早在1962年，Lijima提出来了尺度空间的思想，由于Witkin和Koenderink等人的研究工作，使得尺度空间的思想能够被计算机领域广泛使用[3]。尺度空间的主要是思想是：首先定义一个系数——尺度系数，引入到图像信息处理的模型中，由于尺度系数变化的连续性，会产生很对的尺度描述序列，然后基于轮廓的描述对这些尺度序列进行特征提取，并将提取到的特征数据组合成一种特征向量，进而能够得到图像中相应的边缘信息、角点信息以及不同分辨率上的特征信息等。

尺度空间中是满足视觉不变性的，可以有如下解释：当物体被我们用肉眼观察时，由于背景光强度的不同，图像的光亮被视网膜感知的效果以及对比度是截然不同的，因此分析图像时要求尺度空间算子能够做到不被图像灰度和对比度影响，也就是说在一定程度上满足灰度和对比度不变性。此外，在同一坐标系下，当物体和我们的肉眼观察的发生相对位置变化时，图像位置、大小、角度和形状在我们的肉睛的视网膜上的成像是不同的，所以在进行图像分析时，图像的位置信息、大小信息、角度信息以及仿射变换等信息具备的互不干扰性，也就是满足平移、尺度、欧几里得不变以及仿射不变性。

本文在这里使用一个变换尺度的高斯函数G(x,y,σ)与原图像I(x,y)的卷积和来定义该图像的尺度空间L(x,y,σ)，即：

其中，m×n为模板大小，(x,y)为像素的位置，σ是正态分布的标准差，作为尺度空间描述子，σ的值越大，图像越平滑（模糊），σ的值越小表示图像被平滑的越少，对应的尺度也就越小。这样在分析图像时，图像的全局特征与相对较大尺度的特征图相对应，细节特征则与相对较小尺度的特征图相对应。

接着本文就要对图像进行哈尔分解。首先对图像进行哈尔变换产生多分辨率序列，并以不同分辨率的哈尔特征图为金字塔底层，为了使尺度体现连续性，对每一层的一张图片进行不同参数的高斯模糊，因为每一种分辨率都有三或四种基础特征图，所以多种分辨率的情况下会产生多个金字塔林列，所以在这里引进了金字塔塔林的概念。

2002年，Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯特征提取函数的极值更能产生稳定的特征图像[5]。与非常相似的函数是高斯差分函数（Difference of Gaussian，简称DOG算子）。D(x,y,σ)与的关系可推导如下：

将微分用差分来代替得到如下：

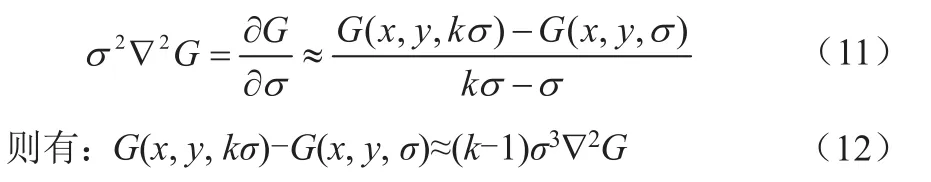
其中，k-1为常数，不影响极值点所在地方。

本文使用效率更高的DOG算子来替代拉普拉斯算子进行极值点的检测，如下：

为了得到高斯差分图像，计算时将上下两层图像的相减，如图2所示，进而进行极值点的检测。

3、特征点的定位和修正

特征点的定位是通过同组高斯金字塔内各DOG相邻之间的比较完成的，按SIFT算法的思想将中间点的像素值和周围26个点作比较，以保证在尺度和二维图像空间都可以检测到极值点。如图3所示。

通过上面步骤检测到的极值点可大致分为两种：强特征性极值点和弱特征性极值点，强特征性极值点的提取是本文的主要目的，而弱特征性极值点的存在往往会对后续的研究工作和应用产生误差。因此本文在引用SIFT特征点修正的基础上，首先利用哈尔变换的去噪机理对DOG图像进行处理，然后将DOG数据进行归一化的处理，并设定合理阈值，最后得到较为整齐的强特征性极值点。

三、特征点描述子选择

在SIFT描述子中，采用加权的梯度方向直方图[6]，维度较高大大地影响了计算效率。随后，Ke等人提出了PCA-SIFT描述子降维后进行匹配[7]。SURF描述子是在SIFT的基础上，计算兴趣点的尺度相关邻域内X和Y方向的哈尔小波，并选择相对邻域内响应最大的作为主方向[8]。Huang等人[9]提出了对比上下文直方图，利用邻域区域的像素强度之间的线性关系进行特征描述，减少局部特征描述的计算时间，但是他仅仅考虑了常量强照度的变化。

本文采用NICD来对本文介绍检测子检测到的特征点进行描述，在将局部邻域内的像素强度规格化后，描述每个子区域中的像素与中心像素的强度对比关系[10]，可得到48维或者64维的特征描述向量。

四、实验结果与分析

1、实验过程

本文在特征点检测试验中采用重复率[11]来评价特征点检测子的鲁棒性。首先对原始图像和变换图像进行特征点的解算，然后求取特征点重复的数量与这两幅图像分别提取的特征点的最小值的比值作为重复率。实际计算中，通过两幅图像提取出的特征点不可能完全的对应，所以，计算时取图像位置小于2i（i为特征点所在不同分辨率的级数，i=0, 1, 2, ……）个像素。此外，实验中采用64维的NICD描述子并用特征点检测时的特征点的梯度和偏移量等对描述子向量进行扩展，构成73维的描述向量。

2、评估标准

采用计算余弦相似度的方法来对描述子向量进行匹配，匹配结果用对应特征点连线图来展示。

3、实验结果

（1）尺度变换匹配实验

本文使用的原始图片为512px×512px，变换后图片为256px×256px。图4分别展示了SIFT和本文所用方法的效果。经过对比可以看出，本文的算子提取的强特征性特征点的数量要优于SIFT算法，进而可以更好地应用于图像局部特征的匹配，另外特征描述子的维度只有SIFT算子的一半，从匹配速度上来说要优于SIFT，从匹配效果上来说和SIFT相当。

（2）尺度和旋转变换匹配实验

在尺度变换的基础上加上旋转变换，效果如图5所示。经过对比可以看出，首先从特征点的数量上来讲要优于SIFT算法，在图像局部特征匹配方面的实用性更强，速度上由于维数的降低要优于SIFT算法，在这种变换情况下，从匹配效果上来讲要略好于SIFT算法。

（3）亮度变换匹配实验

亮度变换匹配实验匹配效果如图6所示。通过对比可以看出，由于NICD描述子的构建过程中，去除亮度的相对干扰，对亮度不敏感，所以匹配效果要明显优于SIFT算法。

本文分别在图像的尺度变换、旋转尺度变换以及亮度变换的情况下进行了特征点的匹配实验，实验表明本文所提的方法有效，满足图像在以上三种情况变换下所提特征点的强特征性不变，并可以有效的应用于图像的局部特征匹配。

五、总结

特征点的强特征性在尺度、亮度、旋转等变换下都可以保持不变，继而成为近年来机器视觉和模式识别的研究热点。本文的思路是将哈尔小波变换和高斯函数相结合，构建金字塔塔林的结构作为特征点的提取工具，引入NICD快速描述子将局部邻域像素规范化，通过对目标区域中特征点与周围像素点之间的规范化强度差进行计算，并结合特征点检测时的特征点的梯度和偏移量等数据合并组成73维的描述特征向量。在实验中分别考虑了尺度、旋转、亮度的变换情况，证明了该算法的有效性。

机器人视觉识别系统都是对局部特征的重要应用，在未来的工作中，我们将把这种特征点检测算法应用到机器人视觉物品识别中，验证它的性能。仿真实验已经证明这种算法的有效性，此外我们还会对该算法进行改进，提出更好的描述子和其搭配用于实时的特征检测和货架商品识别。