基于基因约束算法的电子商务物流路径选取

李 楠

(烟台职业学院 经济管理系，山东 烟台 264670)

电子商务物流路径选取是电商商家最重要的战略问题之一，对电商配送的整体绩效有显著影响.其中，正向物流和逆向物流[1]的过程都共享了大量的资源，逆向物流的路径选取会影响着正向物流路径选取；反之亦然.由于对正向和逆向物流路径分别进行设计会产生局部最优的结果，因此在选取物流路径时，需要联合考虑正向和逆向物流过程.

1 问题描述

为了简化问题，本文考虑图1所示的电子商务物流模型，采用混合整数线性规划(Mixed Integer Linear Programming，MILP)[2]对物流过程进行建模.物流模型采用三种配送方式：第一种，普通配送，指将商品从一个主体配送至相邻的主体处；第二种，直接装运，指厂家直接将商品配送给客户；第三种，直接配送，指将商品从配送中心配送到客户或从厂家配送到零售商.本文的电商物流模型是基于以下的假设：

1)必须满足客户的需求；

2)每个主体的设施数量都是有限制的；

3)同一主体之间不存在配送关系；

4)本文的物流模型有6个主体：供应商、厂商、配送中心、零售商、客户以及收集/检验中心.

本文研究的物流问题描述如下：

前提条件：

1)配送的可用路径集合；

2)客户的需求；

3)需要退货至收集/检测中心的商品数量；

4)从每一个收集/检测中心运送到工厂的退货商品的数量；

5)主体设施的容量.

输入：

1)物流网络的配置；

2)物流配送的最佳路径；

3)每个工厂必须生产的商品数量；

4)将客户分配到配送中心和收集/检测中心的分配方案；

5)向工厂分配供应商的分配方案.

文本的主要贡献如下：联合正向和逆向物流来优化电商物流路径的选择；在物流模型中考虑了三种配送方式，即普通配送、直接装运和直接配送；应用文化基因算法，解决带有容量约束的路径选择问题.

图1 电子商务物流路径模型

2 问题建模

物流模型的目标是最小化物流路径和各个主体运作的成本之和，目标函数如式(1)所示.物流路径的成本是商品在各个主体之间的配送运输成本，包括正向物流和逆向物流(如退货、返修)；主体运作成本是指主体建设和日常运作的成本，本模型仅考虑固定的运作成本.利用混合整数线性规划，建立物流过程的数学模型，如下所示：

(1)

(2a)

(2b)

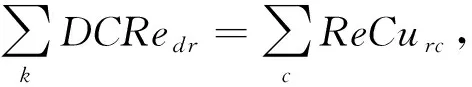
(2c)

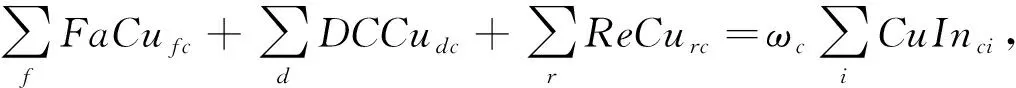
(2d)

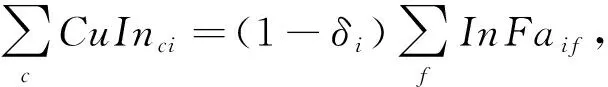
(2e)

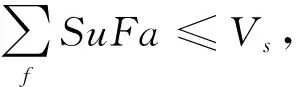
(3a)

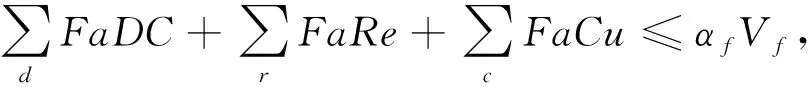
(3b)

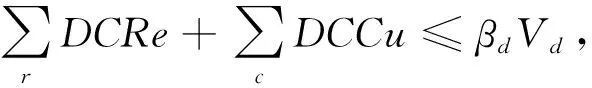
(3c)

(3d)

(3e)

(4)

αf,βd,ηr,μi∈{0,1},∀f,d,r,i

(5)

公式(2～5)是约束条件，约束条件(2a～2e)保证了商品在物流网络中能顺利流通以及需求能够被满足；约束条件(3a-3e)是容量约束，确保了配送到主体的商品不会超过主体的容量；约束条件(4)是为了保证客户的需求能被满足；约束条件(5)是变量的取值范围.

3 基于文化基因算法的模型求解

文化基因算法(Memetic Algorithm)[3]借鉴了遗传算法的精髓，通过加入额外的局部搜索来提高算法寻优的能力.应用文化基因算法求解物流模型(1)的过程如下.

3.1 染色体编码

图2 某客户的染色体编码表示

尽管采用灵活的物流模式可以提高物流配送路径选取的灵活性和效率，但这也会使配送路径选取问题更加复杂.为了解决这样一个NP-hard问题，采用了基于随机路径的直接编码方式，如图2中所示.每个染色体由6个基因构成，染色体表示将商品配送到客户的物流路线，以及从该客户退货的路线.

图2中，染色体的前两个基因是逆向物流的路径，后4个基因是正向物流的路径，基因中的数字是所选主体的编号.使用这种编码方式可能会产生一个不可行的解决方案，即所选的物流路径有可能违反主体的容量约束.因此，在产生物流路径的染色体后必须判断路径的有效性；对于不可行的路径，需要对其进行修复.为了满足客户的需求，每一条物流路径都必须包含至少一个厂商.如果客户的总需求超过了厂商的容量，该客户就会选择另一个容量较大的厂商，这样的分配方式能够实现较低的运输成本.

3.2 染色体解码

通过采用基于随机路径的直接解码方法，可以从染色体中解码出正向和逆向物流的路径.解码的过程如图3所示，使用这种方法可以加快算法的速度.

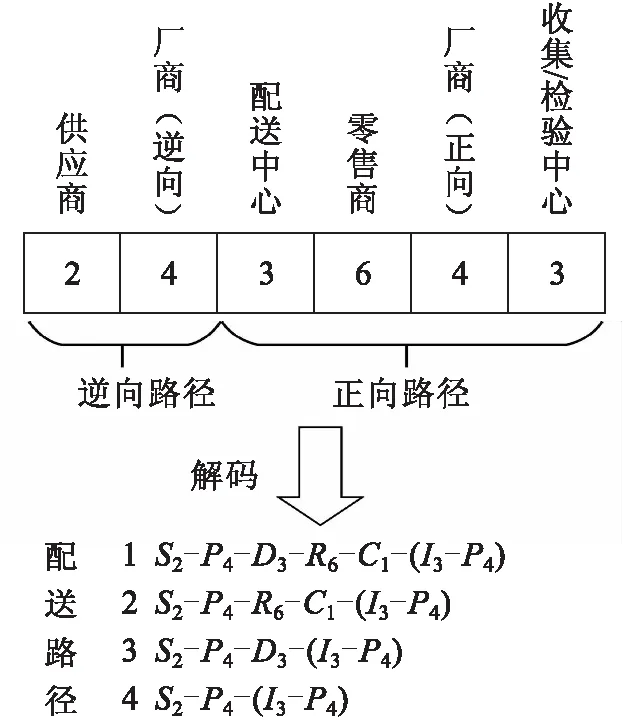
图3 染色体解码

3.3 文化基因算子

采用的文化基因算法算子包括：交叉算子、局部搜索以及选择算子.

交叉算子：本文应用了在遗传算法和文化基因算法中最常用的交叉算子：两点交叉算子(two-point crossover)[4].具体的操作是，首先随机产生两个交叉点，然后将两个染色体中位于交叉点之间的基因进行交换.

局部搜索：在交叉后，会产生两个后代.在随后的局部搜索过程中，利用适应度函数计算后代的适应度值，选择一个更好的后代来进一步改进.利用组合局部搜索，为客户计算最经济的物流路径，选择成本最低的路径.

选择算子：采用比例选择算子(又称轮盘赌选择)来从旧种群中产生下一个种群，使染色体被选择的概率与它的适应度成正比.

4 性能评估

本节通过实验将所提出算法与LINGO软件[5]、ILOG-CPLEX软件[6]进行对比，以评估算法的效率.我们通过将每个阶段的节点数量加倍以产生不同大小的测试集，如表1所示.算法将在每个测试集上运行10次，共进行了50次实验.其他参数使用均匀分布随机生成.实验所采用的PC配置如下：处理器采用Intel酷睿i5 8400 2.8 GHz，内存是金士顿DDR4 2400 GB.

表1 本实验使用的测试样例

为了评估本文算法的有效性和准确性，我们使用功能强大的LINGO软件和CPLEX优化软件求解模型(1)，然后与本文算法的结果进行比较，结果如表2所示.对于测试样例3和测试样例4，在进行了2 000 s的计算后，LINGO软件仍然未能成功求解模型(1)；对于测试样例5也是如此.从表2可以看出，即使是功能强大的LINGO软件也未能解决此类大规模模型，而本文算法却能够做到这一点.采用分支定界法的LINGO并不能解决大规模的优化问题.因此，本文算法还与采用分支裁剪法的CPLEX进行比较，进一步显示本文算法的有效性和准确性.

表2 本文算法与LINGO、CPLEX的实验结果对比

5 结语

本文以最小化物流配送和物流主体运营建设的总成本为目标，建立了物流路径选取的最优化模型；为了解决大规模的物流路径选择问题，采用基于基因约束算法求解该优化模型；分别利用本文的基于基因约束算法、LINGO和CPLEX优化软件求解本文的物流模型，并对结果进行比较，验证算法的准确性和效率.未来的研究集中在以下方面：选择更合适的目标函数，提高物流模型的鲁棒性、时效性等；约束条件需要添加对物流不确定性的考虑；设计更加合理的染色体编码和解码方案等.