学会思考方法快速解决问题

小朋友，你会用一些数学思考方法来解决问题吗？现在，我们一起来学习、解决人教版四年级上册“除数是两位数的除法”的有关数学问题吧，相信你很快就能学会的。

一、分析推理

一些不完整的算式，如果要把不知道的数字补全，使算式完整，就要全面观察算式的特点，合理选择已知条件，运用运算法则，进行分析、推理、判断，逐步淘汰不符合题意的数字，最终准确填出所有的数字。

例1.把下面的算式填写完整。

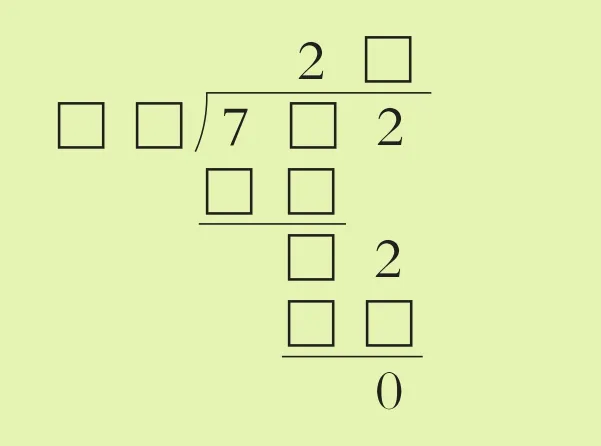
[分析与解]这是三位数除以两位数的除法算式，根据算式的商的十位上的数字是2，被除数最高位上的数字是7，就可以推出除数十位上的数字是3。由最后的两数相减：□2－□□=0，可以推出除数个位上的数字与商的个位上的数字相乘的积的个位上的数字是2，这样就有几种可能：1×2=2，2×6=12，3×4=12，4×8=32，6×7=42，8×9=72。经检验，1×2=2，3×4=12，4×8=32，6×7=42，8×9=72都不符合题意，只有2×6=12符合题意。所以除数的个位上应填6，商的个位上应填2，被除数的十位上应填9。最后把除法算式填写完整如下：

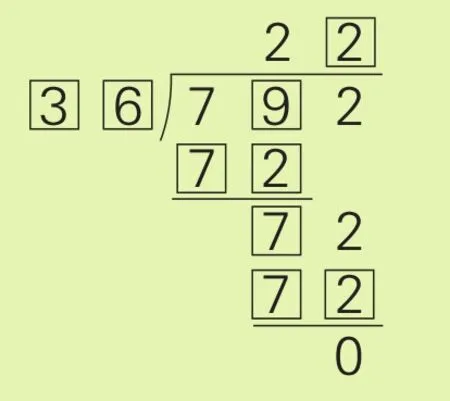
一些小朋友在计算过程中发生错误怎么办？这就需要在错中求解。在解答这类问题时，我们也可以采用分析、推理的方法。首先，要从错误的结果入手，分析其错误的原因，发现变与不变。然后根据加、减法或乘、除法之间的关系，进行计算、推理，最终使问题得到解决。

例2.小华在计算除法时，不小心将被除数末尾的0漏写而使被除数变成18，结果计算得到的商比原来正确的商少54，原来正确的商是多少？

[分析与解]小华将被除数末尾的0漏写而变成18，也就是被除数由原来的180变成18，被除数减少了，而除数不变，这样计算得到的商也随着减少了。因为错误的被除数是18，原来正确的被除数是180，所以错误的被除数比原来正确的被除数减少了180－18=162。又因为计算得到的商比原来正确的商少54，而除数不变，这样就可以求出原来的除数是162÷54=3。因此，原来正确的商是180÷3=60。

二、借助直观

一些题目中的数量关系比较隐蔽，较难理解，如果能结合具体情境或直观图形（线段图、示意图），把题目中的条件和问题形象、直观地表示出来，就有利于找到数量关系，更好地解决问题。

例3.两数相除的商是4，余数是5，被除数、除数、商与余数的和等于94，被除数是多少？

[分析与解]两数相除的商是4，余数是5，说明被除数比除数的4倍还多5，根据题意可以画出下面的线段图，借助直观图来帮助理解数量关系。

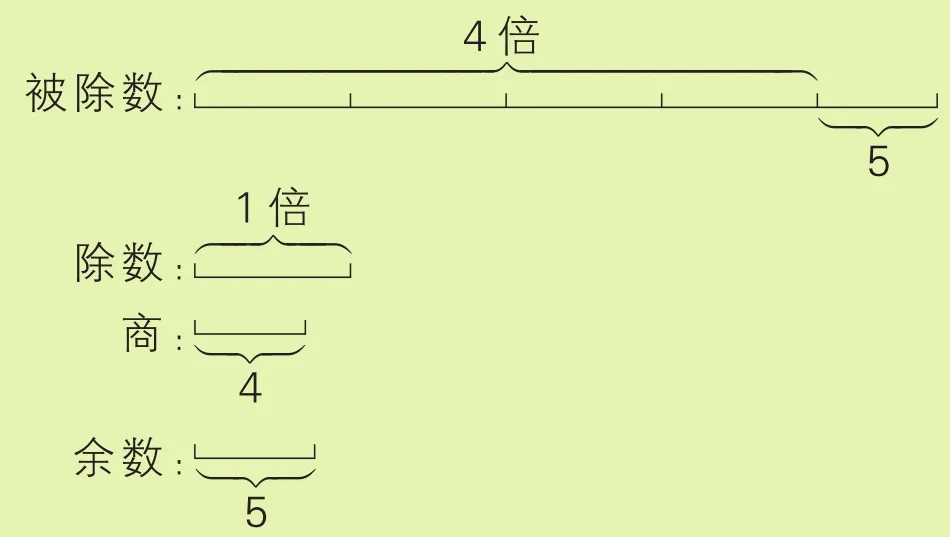
从上面的线段图可以看出，把被除数、除数、商与余数的和分别减去一个商与两个余数后，此时被除数除以除数的商是4，且没有余数，也就是被除数是除数的4倍。知道被除数和除数的和，又知道它们的倍数关系，我们就可以利用和倍关系，先求出除数是（94－4－5－5）÷（1＋4）=16，再求出被除数是16×4＋5=69。

三、运用假设

有些题目有两种或两种以上的数量关系，它们的数量关系比较复杂、隐蔽，如果按照一般的分析思考方法去分析、推理，往往难以找出数量之间的关系。如果我们运用假设法，将题目中的某一个条件假设成已知条件，使题目中隐蔽的数量关系变得明朗、清晰，使比较复杂的条件变得单一，再与其他的已知条件配合，就能比较容易地找到正确的解题方法，从而使问题得到解决。

例4.李老师购买甲乙两种邮票共40张，付出925元。已知甲种邮票每张40元，乙种邮票每张15元，求李老师购买甲乙两种邮票各多少张？

[分析与解]我们可以假设40张全部是乙种邮票，那么购买乙种邮票就需要15×40=600（元）。而购买甲乙两种邮票一共付出925元，这样就少了925－600=325（元）。这是因为甲种邮票每张40元，乙种邮票每张15元，而我们把甲种邮票的价钱当成乙种邮票的价钱来算了，一张乙种邮票比一张甲种邮票少40－15=25（元），因此，可求出甲种邮票的张数是325÷25=13（张）。综合算式为：（925－15×40）÷（40－15）=13（张），乙种邮票的张数是40－13=27（张）。

我们还可以假设40张全部是甲种邮票，那么购买甲种邮票就需要40×40=1600（元），而购买甲乙两种邮票一共付出925元，这样就多了1600－925=675（元），这是因为甲种邮票每张40元，乙种邮票每张15元，而我们把乙种邮票的价钱当成甲种邮票的价钱来算了，一张甲种邮票比一张乙种邮票多40－15=25（元），因此，可求出乙种邮票的张数是675÷25=27（张）。综合算式为：（40×40－925）÷（40－15）=27（张），甲种邮票的张数是40－27=13（张）。