混凝土箱梁零号块水化热温度场分析

李 靓

(苏交科集团股份有限公司，江苏 南京 210019)

对于采用悬臂浇筑施工的混凝土连续梁桥来说，其零号块一般都采用在桥墩上现浇的方法。由于梁体体积较大、水泥强度高，因此在硬化的过程中会产生大量的水化热，常常会导致结构内外温差过大从而引起过大的温度应力使得混凝土开裂[1-3]。因此施工时必须对温度的变化和发展进行必要的预测以便于施工控制。

目前对于大体积混凝土水化热的研究已成为一个重点，并积累了一定的经验，但由于影响水化热的因素较多，且水化热是一个瞬态传热过程，单纯依靠理论公式无法准确计算。随着各种大型有限元软件的广泛使用，该问题得到了很好的解决，其强大的求解功能可以为水化热的研究提供极大的帮助。

本文针对某悬臂浇筑的变截面预应力混凝土连续梁桥零号块，采用大型有限元软件ANSYS对混凝土浇筑全过程水化热进行数值模拟，得到了零号块水化热温度及发展规律，通过与实测结果比较，证实数值模拟的合理性，对研究同类结构水化热提供有益的参考。

1 热传导温度场的计算理论

1.1 热传导方程

混凝土浇筑入模后，在水化热作用下，可以看做是具有内部热源的物体，由于其温度随时间变化是一个瞬态温度场，为简化问题，假设混凝土连续、均匀、各向同性，浇筑后，具有内部热源的箱梁瞬态温度场导热方程为[1-4]：

(1)

式中：a=λ/cρ，称为导温系数。T为混凝土的瞬间温度；Q为热源密度；c为混凝土的比热；ρ为混凝土的密度。由于水化热作用，在绝热条件下的温度上升速度为

(2)

式中：θ为混凝土绝热温升；W为水泥用量；q为单位重量水泥单时间内放出的热量。

根据上式，热传导方程可以改为

(3)

1.2 边界条件

只有热传导方程是无法求出解的，还必须确定方程的初始条件和边界条件。初始条件为在初始瞬时物体内部的温度分布规律，边界条件为混凝土表面与周围介质如空气等之间温度相互作用的规律。

混凝土温度场问题的边界条件通常有3种方式[1，4]：

1)第一类边界条件:混凝土表面温度T是时间的己知函数;

2)第二类边界条件:混凝土表面的热流量是时间的已知函数;

3)第三类边界条件:当混凝土与空气接触时，经过混凝土表面的热流量与混凝土表面温度T和气温Ta之差成正比，即

(4)

式中:Lβ为表面放热系数。

当表面放热系数β趋于无限时，T=Ta，即转化为第一类边界条件。当表面放热系数β=0时，∂T/∂n=0又转化为绝热条件。本文研究的对象为箱梁浇筑过程，由于实际施工时采用钢模浇筑，一般认为钢模是没有保温作用的[2,10]，因此可以忽略模板对热系数的影响，认为混凝土与空气直接进行热交换，属于第三类边界条件。对于表面放热系数β，其大小与结构所处环境的风速大小v和混凝土表面状况有密切关系，根据相关学者研究建议[1]

对粗糙表面:

β=23.9+14.50 v.

(5)

2 工程概况及测点布置

2.1 工程概况

某桥主桥上部结构为(66+110+66)m三跨变截面预应力混凝土连续梁，设计荷载为公路Ⅰ级。主梁截面形式为单箱单室，箱梁梁高按二次抛物线，从跨中3.0 m变化至距主墩中心2 m处6.0 m。主桥箱梁在墩顶零号块处设置厚度为1.0 m的2道横隔板，箱梁顶板宽15 m，底板宽8 m，悬臂长3.5 m，箱梁采用纵、横、竖三向预应力体系。

主桥连续箱梁采用挂篮悬臂浇筑法施工，各单“T”箱梁除零号块采用在支架上现浇外，其余分为12对梁段，如均采用对称平衡悬臂逐段浇注法施工。箱梁纵向悬浇分段长度为(12×4.0 m)，箱梁墩顶现浇块件(即零号块)总长12.0 m。零号块施工采用一次浇筑的方案，由中间像两边对称浇筑。

2.2 测点布置

为了跟踪监测零号块温度场的分布规律，选取截面1、2、3，测试截面位置如图1所示。其中截面1、2为横隔板位置，截面3为距离横隔板2.5 m的外侧箱梁断面。

图1 测点布置断面

测点具体布置位置分别在顶板、腹板、底板、横隔板的内表面、外表面、中部，其中表面测点距离混凝土表面3 cm。测试仪器采用半导体集成温度传感器，温度测量精度为±0.1 ℃。各测试截面测点位置如图2、图3所示，共21个测点。

图2 1-1(2-2)断面测点布置

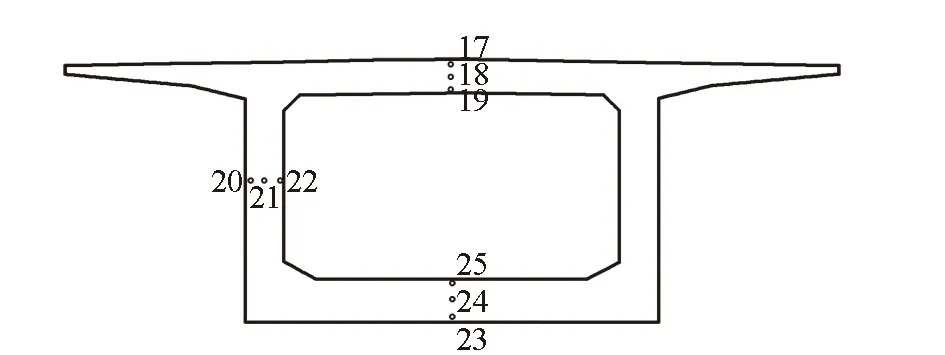
图3 3-3断面测点布置

混凝土入模后即进行温度读数，前4 d每2 h读数一次，后6 d每6 h读数一次。

3 箱梁温度场有限元模型建立

3.1 有限元模型建立

本文运用ANSYS软件进行有限元分析，由于零号块是沿纵向、横向对称的结构，因此为了提高建模的效率，本文只取结构的1/4进行建模分析。采用SOLID 70单元建立实体模型，它是程序中用于进行热分析建立实体模型的单元，具有3个方向的热传导能力。模型采用手动分网，共25 936个单元，30 764个节点，有限元模型如图4所示。

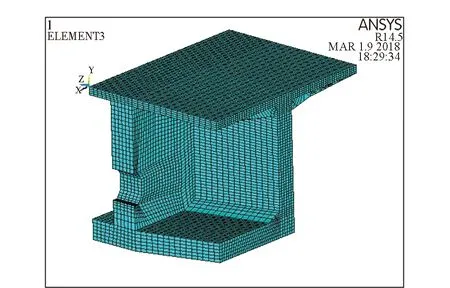
图4 零号块模型

混凝土水化热的分析是一个动态的过程，水泥的放热量、风速、气温等都是一个随着时间变化的过程，为了更方便进行建模计算，提高效率，本文运用ANSYS参数化设计语言APDL的进行建模计算。它可以用来自动完成一些通用性强的任务，为一般问题的求解提供了许多简单高效的手段。

3.2 参数及边界条件选取

根据施工单位采购的材料及实验室参数，得到混凝土材料热参数有密度2 600[ρ(kg/m3)]；导热系数2.7 kJ/(m·h·℃)；比热0.92[kJ/(kg·℃)]。

ANSYS通过定义表面放热系数，将对流边界条件以面荷载的形式施加于实体的外表面。考虑到风速较为离散，难以定量准确地表达，而本项目零号块浇筑时施工现场风速变化较小，基本处于无风或微风的环境，因此各构件表面放热系数β以现场各构件表面风速实测后平均值(如表1所示)来确定。

表1 不同构件处表面放热系数取值

3.3 热源荷载

在温度场计算中，温度是以荷载的形式加载在单元上进行热分析的，对于混凝土结构来说热源是来自水泥的水化热，本文选择目前较为广泛使用的指数型水泥水化热放热公式来描述水泥水化热的放热过程。其计算式[1]如下:

Q(τ)=Q0(1-e-mτ).

(6)

式中：Q(τ)为τ时刻的累计水化热；Q0为τ→时的最终累计水化热。

ANSYS将热生成率施加于单元上，因此对上式求导即可得出生热率表达式

(7)

4 有限元计算结果与施工实测数据分析

图5、图6为主要典型测点温度实测值和有限元计算值的分布曲线，图7为箱梁浇筑2 d后的有限元计算温度场云图。从图7中可以看出在零号块在浇筑过程中，各构件的温度发展具有一定的独立性(各个构件连接处除外)，温度的发展符合大体积混凝土水化热的特征。由于各个构件厚度、散热条件等的不同，温度场发展的规律并不相同。

图5 1-1截面测点1、2、3的实测与计算温度

图6 3-3截面测点18、21、24的实测与计算温度

图7 浇筑2 d后的有限元计算温度场云图

图5为横隔板断面实测值和计算值的分布曲线，可以看到各构件在浇筑后第0.5 d的时候，温度上升很快，各个构件的温度均远大于入模温度26.5 ℃。横隔板中心处，在浇筑后第2 d温度达到最大值，最高温度为约66 ℃，由于体积大、散热条件差浇筑后约15 d温度才接近外界温度。底板在浇筑后1.5 d达到最大值，温度发展规律与横隔板类似，顶板在浇筑后0.5～1.0 d温度达到最大值，由于体积小、散热条件佳，在浇筑后5 d温度接近外界气温值。

图6为距离横隔板外侧2.5 m的3-3断面实测值和计算值的分布曲线，由于该断面各构件体积小，在浇筑后0.5 d内，温度均达到最大值，而后随即进入降温阶段，由于其水化热作用不明显，顶板直接与外界接触，腹板和底板外侧为钢模热交换明显。在浇筑后第4～5 d的时候，外侧顶板、腹板温度场已经接近外界气温，温度趋于稳定。而此时1-1、2-2断面的横隔板、底板，由于体积较大、环境较为封闭，温度仍然较大。

从图5、图6中可以看出实测温度变化曲线与计算曲线较为吻合，最大温差值为3.8 ℃，误差率均小于5%，这说明本桥所建立的有限元温度场模型是合理的，能够较为准确地反应箱梁温度场的实际情况。但值得注意的是顶板实测温度曲线在浇筑后的几天内出现上下震荡，主要原因为顶板厚度小且直接与外界接触，所受环境影响较大，昼夜温差的变化及风速的变化都会造成顶板温度场的变化。而本文有限元模型并未考虑风速及昼夜温差的变化，因而温度曲线较为平滑。实测值与计算值误差率较小，主要由于本项目零号块施工时外界风速及昼夜温差的变化较小。而当这两项外界环境因素变化较大时，有限元模型的建模参数就必须对此予以考虑，否则必然会出现与计算结果的较大差别。此外计算参数的选取与实际混凝土材料必然会存在一定的偏差，这也会使得实测结果与计算值的差别，因此在建立有限元模型前必须对参数的选取进行详细地比较和分析，以确保计算结果的准确性。

控制零号块各构件在水化热作用下的内外温差避免产生过大的温度应力是研究水化热问题的重要目的。根据有限元计算结果，零号块各构件内外计算最大温差为15.3 ℃，结构温差并未预警，因此施工时并未对零号块浇筑做特殊的温控措施，即按常规施工方案进行。实测值中各构件最大内外温差出现在横隔板断面的底板处，温差为16.5 ℃，均满足《大体积混凝土施工规范》的温度控制要求，这也反应了本桥零号块有限元模型结果的准确性。

5 结 论

零号块箱梁体积大、强度高，水化热问题需引起重视，本文采用有限元软件对零号块水化热进行数值模拟分析，并且对零号块典型断面构件的温度场进行实测，结果表明：

1)零号块在浇筑过程中，各构件的温度发展具有一定的独立性(各个构件连接处除外)，温度的发展符合大体积混凝土水化热的特征。

2)同一断面的各构件温度发展规律并不相同，横隔板断面由于体积大、散热条件差，水化热作用最为明显，温度最大值发生在横隔板中心，其在浇筑后第2 d温度达到最大值，底板温度发展规律与横隔板中心相似，降温时间较长。顶板在浇筑后第0.5 d温度达到最大值，浇筑后5 d构件温度接近外界温度。远离横隔板的断面由于构件体积小，散热条件好，升降温都较为迅速，水化热作用并不明显。

3)有限元计算能较为准确的分析箱梁水化热温度场的发展规律，经过比较实测值比较，本文所建立的有限元模型计算结果与实测值较为吻合。