基于空间误差分量Fay-Herriot模型的小域估计

李 腾，魏传华，苏宇楠

(中央民族大学 理学院，北京 100081)

一、引言

近20年来，小域估计(Small area estimation)作为抽样调查领域的一种方法，得到了越来越多的重视。在理论方面，小域估计模型的设定以及有关的估计和检验等统计推断问题得到了深入的研究；在应用方面，小域估计方法已经被广泛使用到了经济、社会、环境、卫生和流行病等多个领域的实际问题中。有关小域估计的详细介绍可参考Rao和Molina的著作[1]。

小域估计方法主要分为两类：基于设计的方法和基于模型的方法。基于模型的方法因能够充分利用其中的辅助信息而得到重视。一般而言，基于模型的小域估计方法所使用的模型一般分为两类，即区域层次模型和单元层次模型，其中区域层次模型使用较多的是Fay和Herriot提出的能将直接估计和未知参数联系起来的一类随机效应模型，文献都称之为Fay-Herriot模型[2]，而关于该模型的理论研究可参考Yoshimori和Lahiri[3]、Benavent和Morales[4]的有关研究。

目前，在关于Fay-Herriot模型的研究和使用上大都假定了各个区域之间是不相关的。然而，很多实际问题中特别是当区域具有空间属性时，区域之间并不独立，而是具有空间自相关特点。为了刻画空间自相关，Singh等人最早将传统Fay-Herriot模型设置为空间误差自相关形式[5]；Pratesi和Salvati在此基础上又给出了小区域估计量的表达式以及对应均方误差的估计[6]；更进一步，Marhuenda等将Pratesi和Salvati的结果推广到一类时空Fay-Herriot模型上[7]。值得注意的是，以上文献关于空间效应的刻画都是通过空间误差自相关形式；而不同于空间误差自相关模型，Kelejian和Robinson提出的空间误差分量(Spatial error component)模型是空间计量经济学中用来刻画空间自相关的另外一种常用方法。该模型将模型误差分解为相互独立的两部分，即空间溢出项和非空间溢出项，能够直接有效地刻画观测单元之间的相互影响，弥补了空间误差自相关设定的不足[8]。为了更好地刻画抽样区域之间的空间相关性，本文将在传统Fay-Herriot模型的基础上考虑将模型误差设定为空间误差分量形式，提出一类空间误差分量Fay-Herriot模型，以研究相应的小域估计量的构造及其性质。

二、目标参数估计量的构造

(一)模型构建

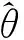
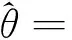
(1)

其中e为抽样误差，期望为0；协方差矩阵为ψ，且ψ=diag(ψi)是已知的。假设目标参数与辅助变量之间存在某种线性关系：

θ=Xβ+Wu+ε

(2)

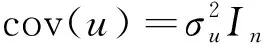
将上面两个模型相结合，就可得到如下的空间误差分量Fay-Herriot模型：

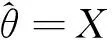
(3)

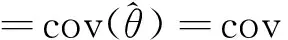
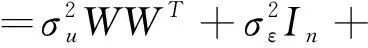
(4)

(二)参数估计

基于以上模型，根据混合线性模型的理论可知，未知固定参数β的最佳线性无偏估计量(BLUE)和随机效应u的最佳线性无偏预测(BLUP)分别为：

(5)

(6)

从而第i个区域目标参数的最佳线性无偏预测估计可记为：

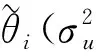
(7)

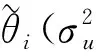
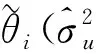
(8)

(三)协方差参数的估计

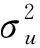
1.ML算法

1)计算极大似然函数：

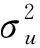
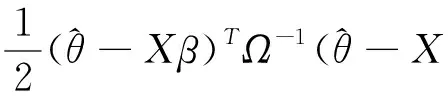
(9)

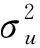
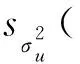
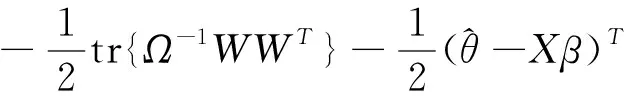
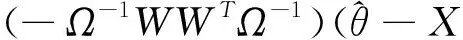
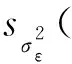
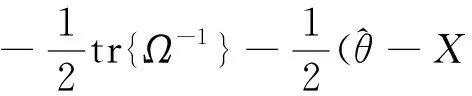
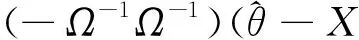
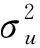
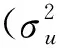
(10)

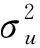
(11)

2.REML算法

1)计算边际似然函数：

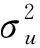
(12)

其中P=Ω-1-Ω-1X(XTΩ-1X)-1XTΩ-1

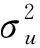
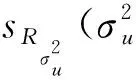
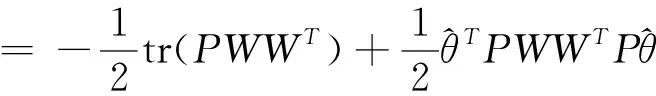
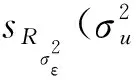
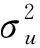
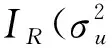
(13)

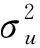
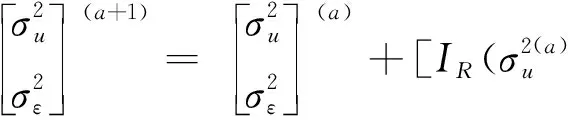
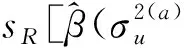
(14)

三、小域估计量的均方误差及估计

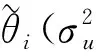
(一)BLUP的MSE

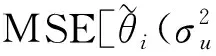
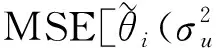
(15)

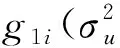
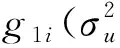
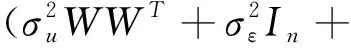
(16)

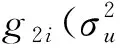
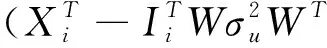
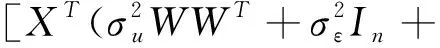
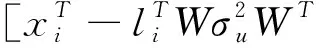
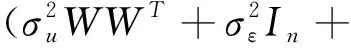
(17)

(二)EBLUP的MSE

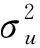
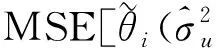
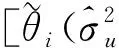
(18)

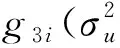
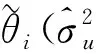
因此

进而有

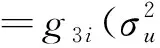
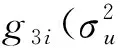
(三)EBLUP的MSE估计

通过Harville和 Jeske[11]、Zimmerman和Cressie[12]的研究可得如下结论：

1.采用ML算法时小域估计量MSE的估计

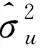
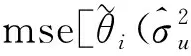
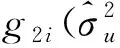
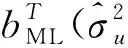
2.采用REML算法时小域估计量MSE的估计

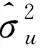
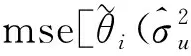
四、数值模拟

本部分采用数值模拟考察所提方法的有效性。为进行比较，模拟实验分别考虑在协方差参数已知和未知的情况下估计模型参数。首先假定研究区域是边长为m-1个距离单位的正方形，n个空间观测单元正好在m×m个格子点上，考虑如下模型：

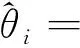
(i=1，2，…，n)

(19)

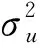
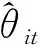
以上公式可整理为：

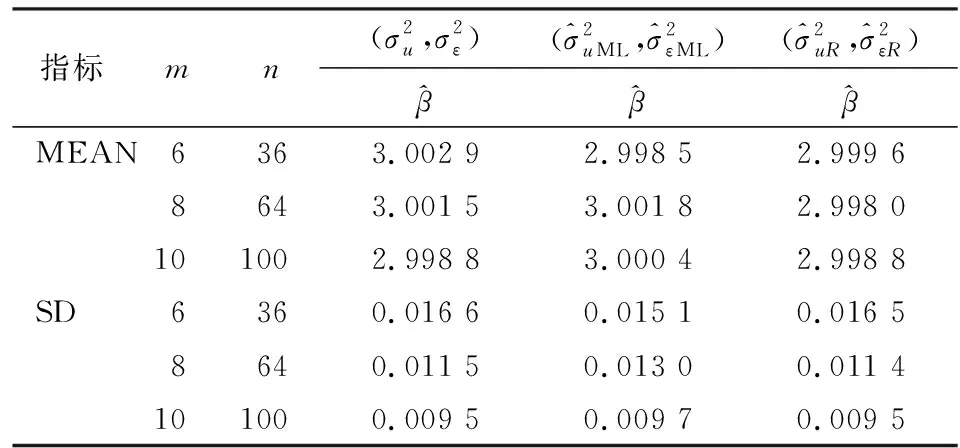
表1 参数β估计结果表

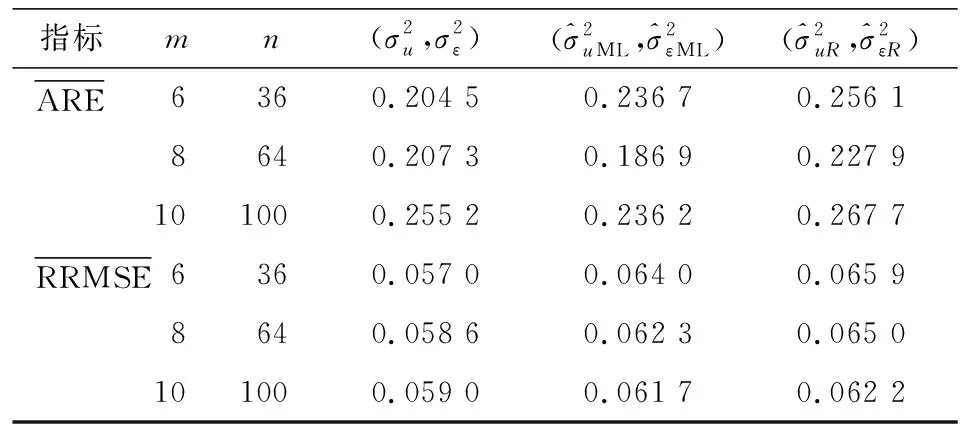
表2 小域估计量指标对比表

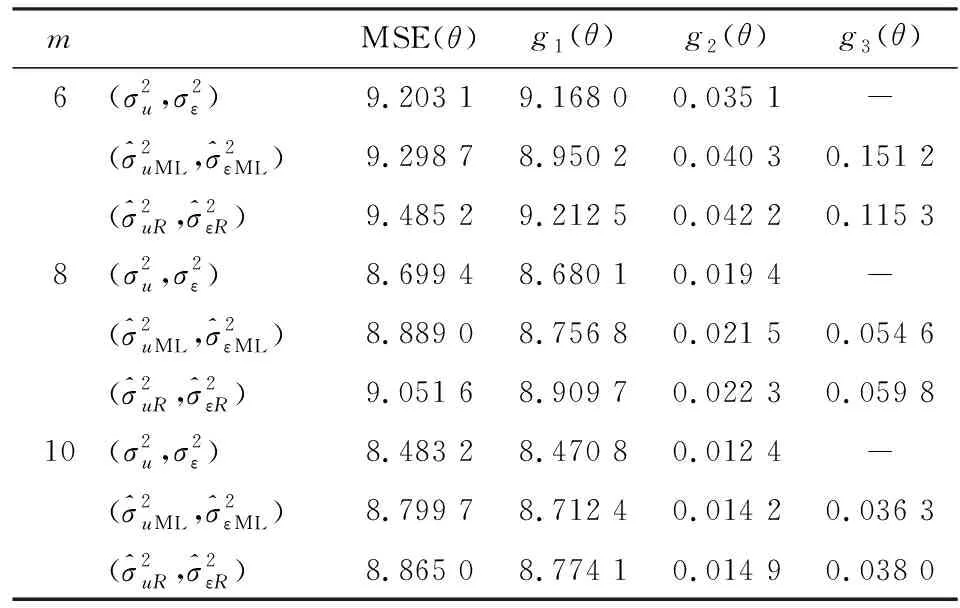
表3 小域估计量均方误差均值比较表

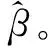
五、总结与展望

为了更好地刻画区域之间的空间效应，本文提出了一类空间误差分量Fay-Herriot模型用于小域估计，并给出目标参数的估计以研究其均方误差的估计问题，通过数值模拟验证了所提方法的有效性。本文结果推广了小域估计的现有模型。

作为一类区域层次模型，类似于Marhuenda等的研究[7]，本文方法同样可以推广到具有多个时间点观测的情形。此外，吕萍和郭淡泊讨论了域的样本量分配问题，并结合小域估计模型在计划域的情况下讨论样本量的分配问题[13]，这也是值得研究的。