经济社会调查中的空间平衡抽样设计

郝一炜，金勇进

(1.中国人民大学 a.统计学院，b.应用统计科学研究中心，北京 100872；2.首都医科大学附属北京地坛医院 病案统计科，北京 100015)

一、引言

空间抽样这一概念起源于对自然资源的调查，例如矿藏的寻找、土壤成分的分析、空气污染的检测和物种的多样性调查等等。这类调查有两个显著特点：一是由于被调查总体通常是在空间中连续分布的无限总体，因此难以划定抽样框；二是总体单元之间存在空间相关性，例如在对土壤中某种金属元素含量进行调查研究中，某种金属含量高的土壤往往呈现出空间上的集中分布。为了解决上述问题，地理学家利用地理信息系统(GIS)将地理空间切割成规则的正多边形，构造出空间中的随机网格，基于该种空间切割对划分后的空间子区域进行随机抽样并进行统计推断。空间抽样在地质、环境、生态、海洋、气象等领域得到了广泛的应用，但是经济社会调查中的空间抽样方法仍有待发展和研究。

与地理学所研究的对象相似，经济社会调查的总体单元之间同样普遍存在空间相关性。例如：高档商铺的分布集中在繁华商圈、高新技术企业的分布集中在技术产业新区、优质医疗资源的分布集中在经济发达地区等等。空间相关性的存在导致空间上相邻单元的目标变量数值之间高度相关，破坏了传统抽样调查设计中总体单元之间独立性的假定，此时传统抽样设计的应用将面临巨大挑战。例如，对某地区餐饮店铺人均消费的调查中，研究总体为该地区的全部餐饮店铺，高消费的餐饮店铺多数坐落在繁华商圈，而农村地区的餐饮店铺人均消费会在一定程度上低于城镇地区。如果不考虑总体的空间特性，样本的随机性可能导致抽取到的商铺集中分布在某些区域，而其他区域的商铺则没有进入样本。如果入样的商铺恰好集中分布在繁华商圈，那么基于这样的样本进行推断将会高估人均消费情况。由此可见，在方案设计中忽视总体单元的空间位置信息将导致样本单元空间位置分布无法对整个空间形成均匀覆盖，样本代表性下降，估计效率随之下降。因此，当经济社会调查的总体存在空间相关性时，应当考虑使用空间抽样设计消除总体单元之间空间相关性的影响，获取代表性更好的样本。

空间平衡抽样是地理学空间抽样中空间切割划分后的一种样本点选择方法，其主要思想是利用空间辅助信息设计抽样算法，使得样本点的空间分布更加分散、更加均匀。在经济社会调查中，可以借鉴地理学中的空间平衡抽样设计进行抽样，利用总体单元的空间位置信息对抽样设计进行改进，解决传统抽样设计面对空间总体时所面临的难题。

学者们关于空间平衡抽样方法的研究取得了一些成果，Stevens等提出广义随机棋盘分层法(GRTS)，并将其应用到自然资源的调查当中，其思路是利用一个函数将二维空间的坐标投影到一维空间并基于一些限制条件加以随机排序，然后使用系统πPS抽样对一维空间上的样本进行样本点选择，进而使入样单元在空间上尽可能地分散[1]。姜成晟、王劲峰等总结了几种主流的地理学空间抽样中的样本点选择方法，并认为GRTS抽样并不是一种严格的样本点布局方法，因为该种方法改造了样本空间的结构[2]。Dickson等认为GRTS方法并不完美，因为空间重构会导致一维空间中的样本次序存在不确定性，样本点排列次序的不同会对二阶包含概率产生影响[3]。基于GRTS法存在的缺陷，学者们提出了空间平衡抽样设计的改进方法。Grafström提出了空间相关泊松抽样法(Spatially Correlated Poisson Sampling)，该种方法利用预设的距离函数对包含概率进行更新，使空间上距离较近的单元倾向于不同时进入样本，进而抽取到在空间上具有平衡性的样本[4]。Grafström等介绍了局部枢轴法(Local Pivotal Methods)在空间平衡抽样设计中的应用，在实际应用中有LPM1和LPM2两种算法[5]，前者抽取的样本点分布更加均衡，后者计算速度更快。Grafström等将局部枢轴法的思想与立方体法(Cube Method)进行结合，提出了空间双重平衡抽样法(Doubly Balanced Spatial Sampling)，又称局部立方体法(Local Cube Method)[6]。其思路是在总体空间中抽取一系列空间子集，在子集内部使用立方体法的起飞步(Flight phase)和着陆步(Landing phase)进行抽样。

空间平衡抽样能够保证样本点在空间中尽可能分散，具有这种特性的样本具有空间平衡性[7]。面对经济社会调查中总体单元存在空间相关性的问题，本文提出了借助地理学中的空间平衡抽样算法进行空间平衡抽样设计，使空间上距离较近的单元倾向于不同时进入样本，保证样本单元在空间上均匀分布，提高样本的代表性，提高估计效率。在实践中，可以在构造抽样框时采集总体单元的经纬度坐标做为空间辅助信息，进而实现空间平衡抽样设计。经济社会调查中的总体单元通常在空间中离散分布，不需要空间切割等复杂的事前处理，在实际调研中简洁实用。

二、以总体单元经纬度坐标为空间辅助信息的空间平衡抽样设计

(一)空间辅助信息

空间辅助信息是指空间抽样设计中所使用的总体单元的空间位置信息。空间辅助信息在经济社会调查中普遍存在，实践中可以获取的空间辅助信息有如下形式：

1.总体单元的行政区划

行政区划是最简单直观的空间辅助信息形式，例如：总体单元的区县、街道乡镇以及社区等等，实践中行政区划辅助信息的收集较为便捷，在大型调查项目中应用广泛。传统抽样设计中，总体单元在不同区域的规模差异可能较大，设计人员常使用行政区划作为分层标志对总体加以分层，以保证层内单元差异较小而不同层单元之间差异较大，该种思路可以视为对空间辅助信息最朴素的利用方式。

2.总体单元的经纬度信息

经纬度坐标信息不但能锁定总体单元的空间位置，还能获取总体单元之间的相对位置和空间距离。作为一组二维定量辅助变量，经纬度坐标比行政区划和街道乡镇等定性辅助变量提供了更加丰富而精细的统计信息。实践中可以利用总体单元的经纬度信息作为空间辅助信息对抽样设计加以改进，构建空间平衡抽样设计，从而达到提高样本代表性和提高估计效率的目的。

(二)空间平衡抽样设计

在经济社会调查中，空间平衡抽样设计在抽取样本时考虑了总体单元的空间位置信息，并利用算法更新总体单元的包含概率，使空间上距离较近空间相关性较强的单元倾向于不同时被选入样本，从而保证获取到在空间中均匀覆盖的样本。其设计方法如下：

1.抽样框构造

明确调查总体并构建包含有总体单元经纬度坐标作为空间辅助信息的抽样框，经纬度信息的获得可以借助网络地图PC端软件、在线地图软件以及手机APP。

2.初始包含概率设定

为总体单元设置初始的包含概率πi，可以采用等概率设计，亦可采用不等概率设计。

3.利用空间平衡抽样算法进行样本选择

空间平衡抽样算法将总体单元的预设包含概率更新为入样指示变量，也即所有的预设包含概率被更新为非0即1的数值，入样指示变量为1表示该单元进入样本，反之亦然。在此过程中，总体单元的经纬度信息将被用于计算单元之间的空间距离，这体现了空间平衡抽样算法对空间辅助信息的利用。实践中有如下3种算法可供使用：

(1)空间相关泊松抽样(SCPS)

SCPS算法对总体单元进行N次逐一访问，每一步运算将当前访问单元的包含概率更新为0或1的入样指示变量，每一步更新都基于上一步更新的结果进行。包含概率的更新利用了Bondesson等提出的相关性泊松抽样法(CPS)[8]，该种抽样方法依照单元的排序使用包含概率更新规则对单元进行逐个访问，其更新规则为：

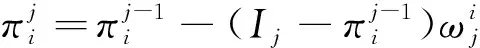
(2)局部枢轴法(LPM)

LPM算法具体分为LPM1算法和LPM2算法。LPM1算法对包含概率进行成对更新，其过程是从总体中随机抽取一个单元，再选取其最邻近的单元。如果这两个单元互为最邻近单元，则为这两个单元赋予高度负相关的包含概率，进而使空间上临近的单元同时入样的可能性降低。该种算法对包含概率的更新借助了Deville和Tillé提出的枢轴法[9]，每次随机抽取i和j两个单元的情形下，包含概率组(πi，πj)将按照如下规则更新，对于所有总体单元的包含概率更新在每个单元的包含概率都取0或1之后结束：

πi+πj<1

(π'i，π'j)=

LPM1算法借助空间辅助信息“锁定”了一对空间上距离最近的一对单元进行包含概率更新，其算法由“随机抽样”、“计算距离”和“包含概率更新”三步构成，理论上最大的运算次数为N3次。

LPM2算法与LPM1算法的区别在于，LPM2算法在随机抽取到一个单元和其最邻近单元后，不要求这两个单元互为最邻近单元，而是直接使用枢轴法对单元之间的包含概率进行更新，因此LPM2算法的最大运算次数为N2次。LPM2算法获取样本的空间平衡性不及LPM1算法，但是降低了运算的时间和次数。

(3)空间双重平衡抽样(DBSS)

DBSS算法又称局部立方体算法，其过程是在总体空间中重复抽取空间子集，并在子集内部抽取空间平衡样本，该算法每一次重复计算有两个步骤：

第一步，抽取总体空间的一个子集，抽取该子集的算法步骤是：①在尚未被算法访问的集合中随机抽取一个单元，以及距离该单元最近的p个单元组成子集；②计算上一步子集的中心点以及子集中单元距离中心点的距离平方和；③选取距离上一步计算中心点最近的p+1个单元组成新子集，并重复寻找中心点和距离平方和的计算，直至新确定的子集内距离平方和不再下降为止。由此，一个空间子集得以确定。

第二步，在上一步确定的子集内利用经纬度坐标作为平衡变量构造平衡方程，使用立方体法(Cube Method)的起飞步[10](Flight Phase)进行抽样，样本需要满足平衡条件：

其中，k为样本序号，Ik表示入样指示变量，πk是初始包含概率，xk是经纬度坐标构成的二维向量。

重复上述计算，每一次将有p+1个单元被决定是否进入样本，当最后一次剩余的单元数不足p+1个时，使用立方体法的着陆步(Landing Phase)对剩余单元进行抽样。DBSS算法借鉴了局部枢轴算法中的“空间局部计算”思想，并将立方体法与之结合，获取到具有空间平衡性的样本。

4.基于抽样结果开展调查

依照调查的实际需求，通过实地调研或资料查阅等方式采集样本单元的目标变量，并将结果汇总。

5.基于空间平衡样本进行统计推断

空间平衡抽样算法对包含概率的更新本质上是一个“选样”的过程，更新后的入样指示向量以数值1和0表示单元是否进入样本。入样指示向量是在空间辅助信息作用下随机抽样结果的“汇总”，并不能将其当做包含概率来对待。对于某个总体单元来说，更新后的入样指示变量无论是0还是1，都是其初始包含概率在空间辅助信息下随机实现的结果。因此，在估计阶段，估计量中使用的是初始设定的包含概率，而不是入样指示变量。由此可见，空间辅助信息的作用体现在“选样”的阶段，没有在“估计”阶段使用。

空间平衡抽样对等概率和不等概率情形同样适用，可以采用经典的赫尔维兹-汤普森(HT)估计量和简单方差估计量，总体总值的估计量以及方差估计量形式为：

(三)空间平衡抽样设计的适用性

实践中，只要总体单元具有能够唯一识别的空间位置坐标，例如企业、商铺、行政区、社区、学校、医院等等，都可以使用空间平衡抽样设计。如果总体单元之间存在空间相关性，那么空间平衡抽样设计相较于传统抽样设计能够获得代表性更好的样本。空间平衡抽样虽然不能直接应用在研究对象是“个体”或“住户”的调查中，但是这类调查经常采用多阶段抽样设计，可以利用社区街道或工作单位的空间信息构建初级抽样单元抽样框，采用空间平衡抽样设计抽取初级抽样单元。例如，对家庭收入的调查中，高收入者会集中居住在高档社区，利用空间平衡抽样设计抽取社区可以获取代表性更好的初级抽样单元。可见，在人口、资源、住户、商业等抽样调查所涉及的领域中，空间信息的普遍存在为空间平衡抽样的发展和应用提供了广阔的空间。

三、实证研究

为了研究空间平衡抽样设计在经济社会调查中的应用，本文使用北京市各区县590家医院实有病床总数的抽样调查进行实证分析。总体中的590家医院包含了由医疗主管部门评级的各级别公立医院和私立医院，不包括未评级医院，不包括社区卫生服务中心以及部分护理院、研究机构、卫生监督机构和卫生行政机构。590个总体单元中包含373家一级医院和217家二三级医院。北京市卫生统计汇编材料上记载了全市各级医疗机构的床位数，因此590个总体单元的目标变量真值已知，由此可以借助R语言编程实现大量多次重复抽样运算，以对比空间平衡抽样设计和传统抽样设计的优劣。

(一)抽样方案设计

1.含有空间信息的抽样框构造

590个总体单元的名录可以从医疗主管部门的评级名录中获取，经纬度辅助信息借助某互联网公司旗下在线地图中的经纬度坐标拾取功能来获取。本文仅就等概率场合下的抽样进行研究，各个单元依照样本量要求被赋予相同的包含概率。至此，包含总体单元名录和经纬度坐标作为辅助信息的抽样框构建完成。

图1直观地展示了总体单元的空间分布，很显然北京地区的医院主要集中在中心城区，如果将总体单元分成一级医院和二三级医院两部分考察，二三级医院呈现出更加明显的空间聚集特征。

图1 北京地区590家医院空间分布图

对比图2和图3可以发现，一级医院和二三级医院都呈现出在城中心集中分布的趋势，但是一级医院的密度由中心向外扩散下降的过程更加平缓，二三级医院主要集中在中心城区。显然，该总体的单元之间存在规模差异，总体单元的目标变量之间存在显著的空间相关性，也即床位数较多的大型医院呈现出空间聚集特征。

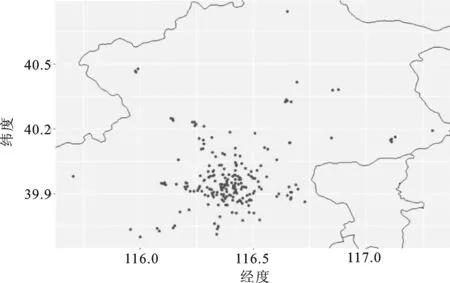
图2 北京地区217家二三级医院空间分布图

图3 北京地区373家一级医院空间分布图

2.样本量的确定

实证分析中将分别基于固定样本量和变动样本量对几种抽样方法进行对比。固定样本量场合下按照简单随机抽样的样本量要求抽取容量为300的样本，变动样本量场合下对比样本量从小到大变化情况下各种方法的估计效率变动情况，不再设置固定的样本量。

3.样本的获取方法

为了对比空间平衡抽样设计与传统抽样设计的优劣，本文基于前文中构建的抽样框分别使用如下抽样方法进行抽样。

分层随机抽样。该案例中总体单元的规模差异可由医院级别来进行刻画，因此可采用分层抽样设计来改进估计量的统计性质，以医疗机构的级别(一级/二三级)作为分层标志，使用比例分配确定各层样本量，借助传统的分层随机抽样提高样本对总体的代表性。

简单随机抽样。虽然统计学家已经证明分层随机抽样的估计效率优于简单随机抽样，但是不妨将简单随机抽样应用在实证分析中作为估计效率对比的参照。

空间平衡抽样。本文在实证研究中使用SCPS、LPM1和DBSS算法进行空间平衡抽样，利用总体单元的经纬度作为空间辅助信息，进而通过抽样算法计算距离，抽取空间平衡样本。由于LPM2算法与LPM1算法存在相通性，因此本文仅以LPM1算法作为局部枢轴法的代表。三种空间平衡抽样算法具体的操作步骤如下：

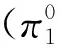
(2)LPM1算法。将590家医院编号，假定此刻的包含概率向量为(π1，π2，…，πN)，也即初始包含概率。首先随机选取总体中的1家医院，假定为Xi，然后计算该医院与其他医院的空间距离，选取其中最邻近的医院Xj。利用前文所述的枢轴法更新规则对上述两家医院的包含概率进行更新，其中1家医院的包含概率被更新为0或1。不妨假定，上述运算之后Xj的包含概率被更新为1，则医院Xj进入样本，不再参与计算。如此重复进行运算，经过至多N3次计算后，所有医院的包含概率都被更新为0或1，包含概率向量(π1，π2，…，πN) 被更新为入样指示向量(I1，I2，…，IN)，入样指示变量为1的相应医院进入样本。

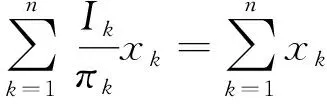
上述抽样方法计算量较大，可借助R软件以及软件中的Balanced Sampling程序包来实现，利用R语言编程并运行程序即可获得样本并进行估计。

4.基于样本进行估计

采用HT估计量对总体总值进行估计，采用简单估计量对总体总值估计量的方差进行估计，估计量的表达式可参考前文所述，此处不再赘述。

(二)估计结果对比

1.相同样本量下空间平衡抽样与传统抽样方法的对比

由于总体总值量纲数值较大，本文采用估计量标准差对估计效率进行对比。各方法总体总值和估计量标准差在1 000次重复抽样后的均值如表1所示。

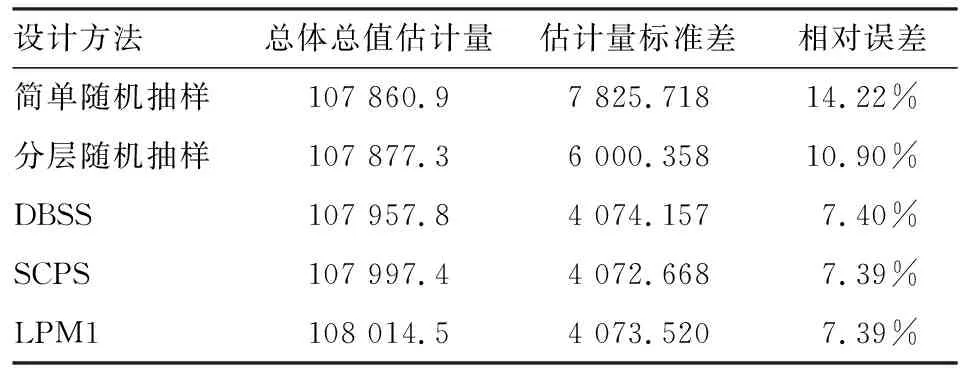
表1 1 000次抽样的估计结果均值

由HT估计量的性质可知，实证分析中使用的5种方法都能够做出总体总值的无偏估计，这一点在表1汇总的实证分析估计结果中可以体现，而且空间平衡抽样设计的估计量标准差相比传统抽样方法有明显的降低，相对误差也随之下降。与此同时，1 000次空间平衡抽样设计的估计量标准差相比传统方法更为稳定。

由图4可见简单随机抽样估计量标准差在8 000左右呈现较大幅度的波动，分层随机抽样估计量标准差在6 000左右呈现较大幅度波动，三种空间平衡抽样设计的估计量标准差则稳定在4 000左右，标准差变动曲线几乎重合。为了清晰地展示3条几乎重合的折线，图5单独绘制了空间平衡抽样算法的估计量标准差变动情况。

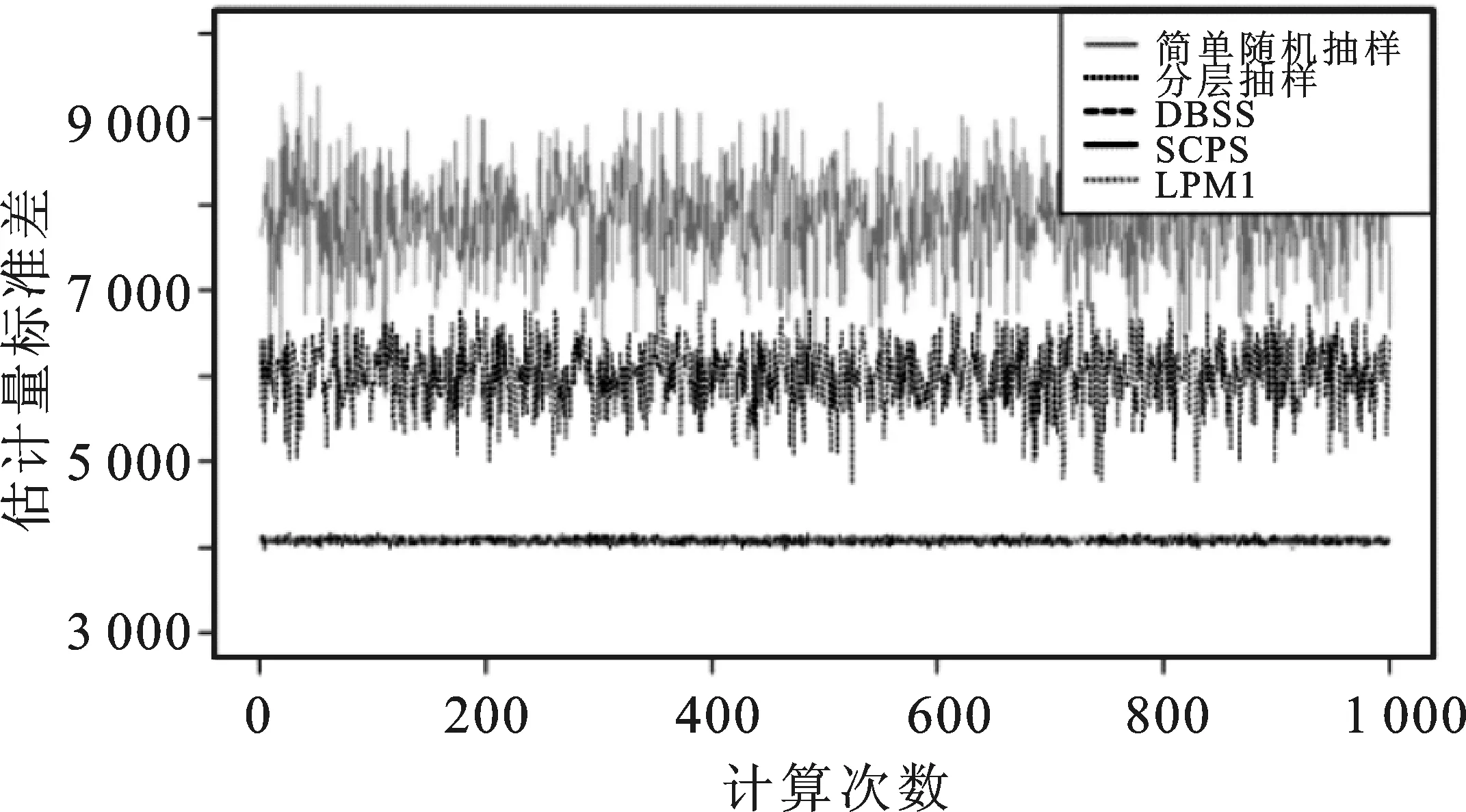
图4 不同抽样方法估计量标准差图

实证研究的结果表明，当空间坐标辅助信息存在的情况下，空间平衡抽样在总体单元存在空间相关性的经济社会调查中能够获得比传统抽样方法统计性质更加优良的估计量。

2.不同样本量下空间平衡抽样与传统抽样方法的对比

前文中提到，由于实证分析中的总体单元规模差异较大，也即总体方差较大，传统的抽样方法在应用中需要较多的样本量。空间平衡抽样能够显著地降低估计量方差，在实际应用中能够相应地降低对样本量的要求，在一些大型调查项目中能够达到控制成本的目的。为了对这一结论加以佐证，本文利用R语言编程研究了样本量连续变化时，各种抽样方法1 000次抽样平均估计量标准差的变动情况。由于简单随机抽样在前文的实证分析中已经被证明是一种效果很差的方法，因此本次方法间的对比不再包括简单随机抽样。图6展示了样本量逐渐增加时，使用各种抽样方法进行1 000次随机抽样的平均估计量标准差变动情况。

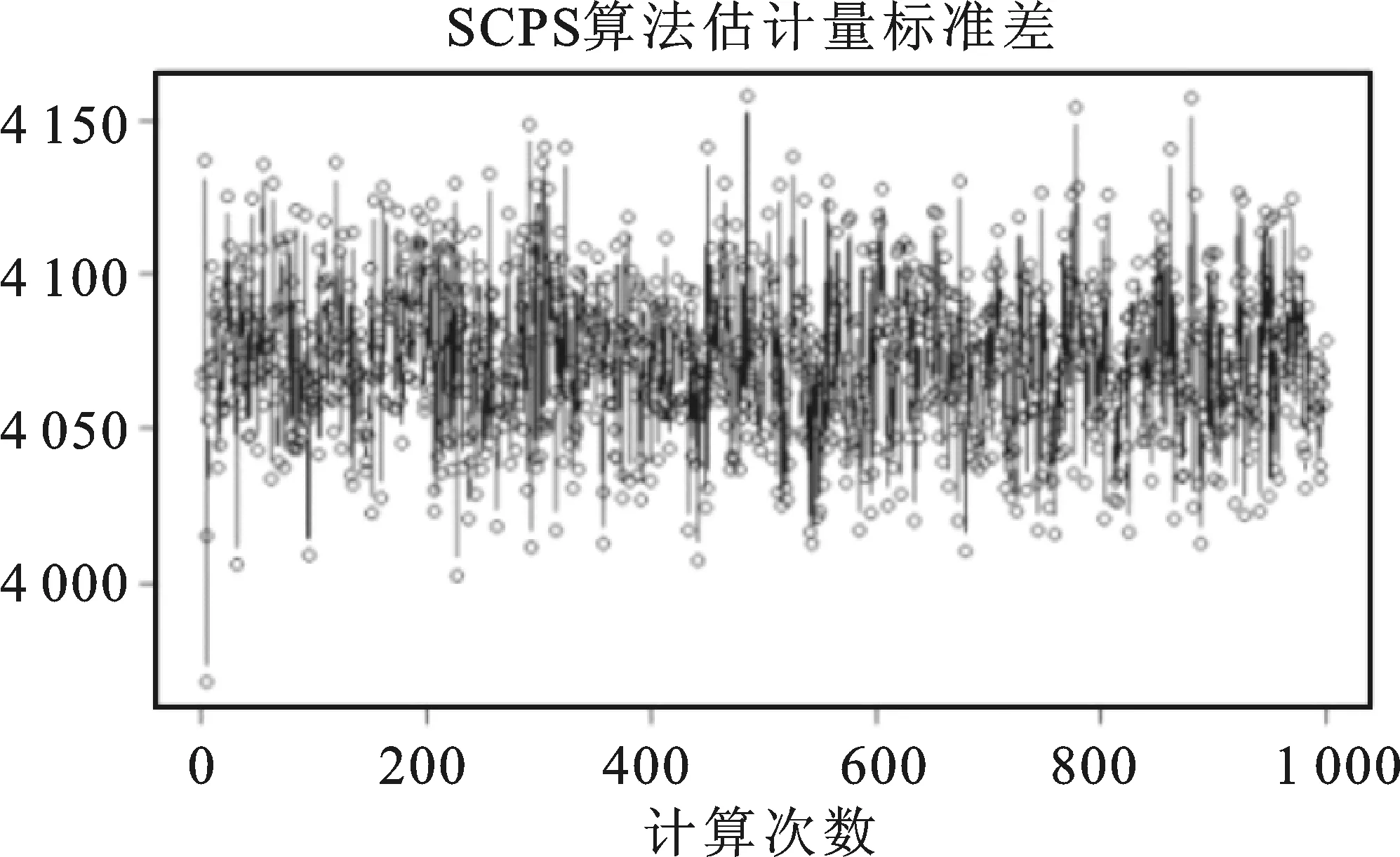
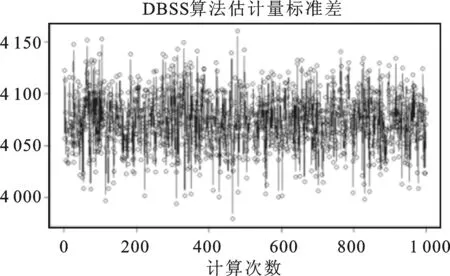
图5 3种空间平衡抽样算法估计量标准差变动图

图6 不同方法下估计量标准差随样本量变动图

由图6可见，各种方法的估计量标准差随着样本量的增大均呈现出下降趋势，3种空间平衡抽样方法的曲线几乎重合。为了清晰展示3条几乎重合的折线，图7单独绘制了空间平衡抽样算法的平均估计量标准差随样本量变动的情况。

结合图6和图7可见，样本量较小时，空间平衡抽样设计的标准差平均值显著低于分层抽样。随着样本量增大，空间平衡抽样设计估计量标准差下降的速度略低于分层抽样，四条曲线逐渐逼近。当样本量超过500后，分层抽样的估计效率超越空间平衡抽样。也就是说，当抽样比非常接近1时，分层抽样的平均估计量标准差比空间平衡抽样先缩减至0。但是，实践中几乎不会使用如此高的抽样比，因此空间平衡抽样设计在各种样本量下均能够得到比分层抽样统计性质更加优良的估计量。特别是在小样本情况下，空间平衡抽样设计相比分层随机抽样能够显著地降低估计量标准差。

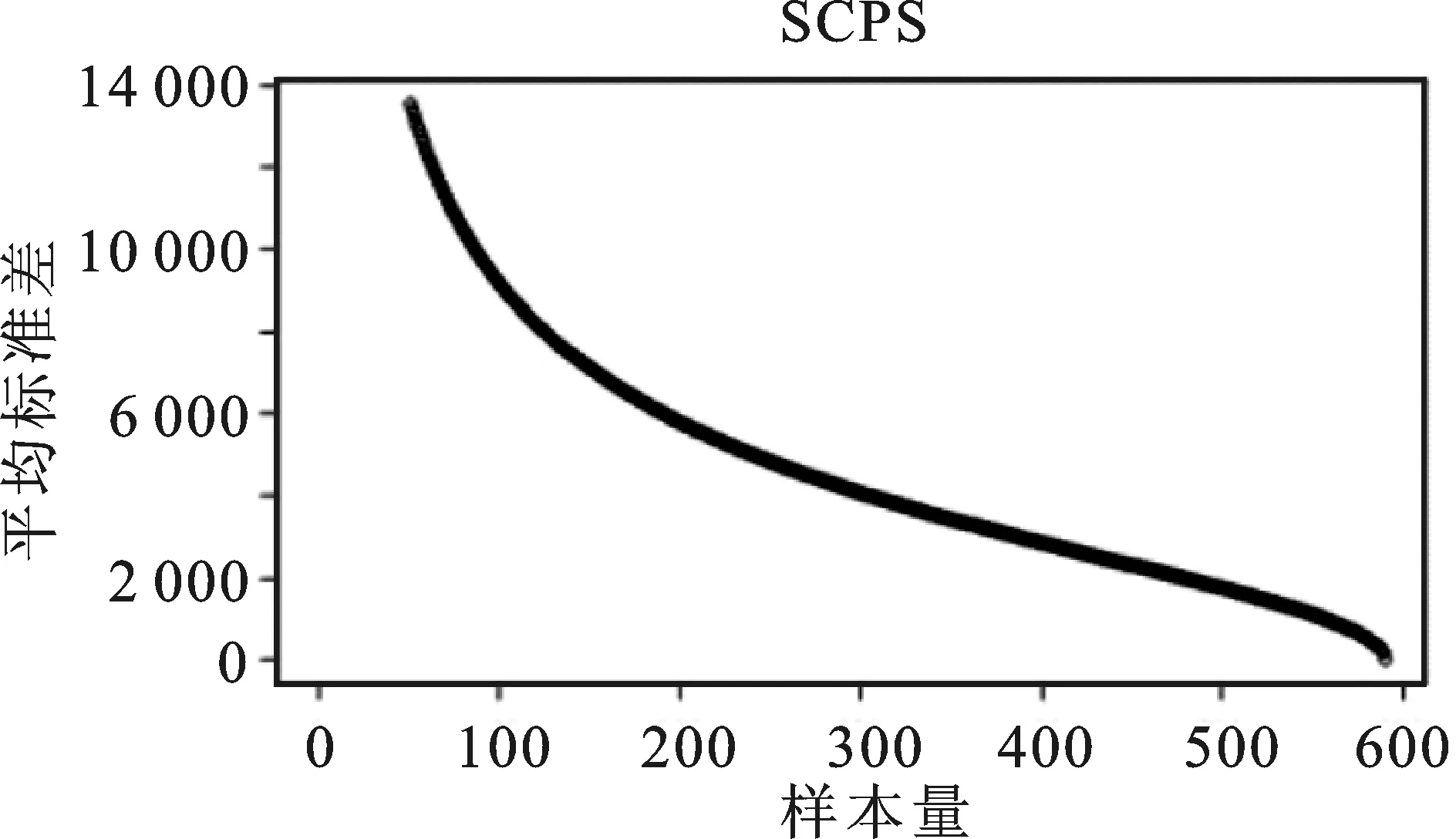
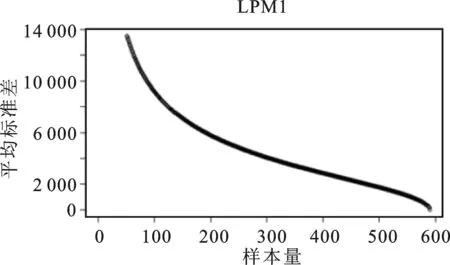
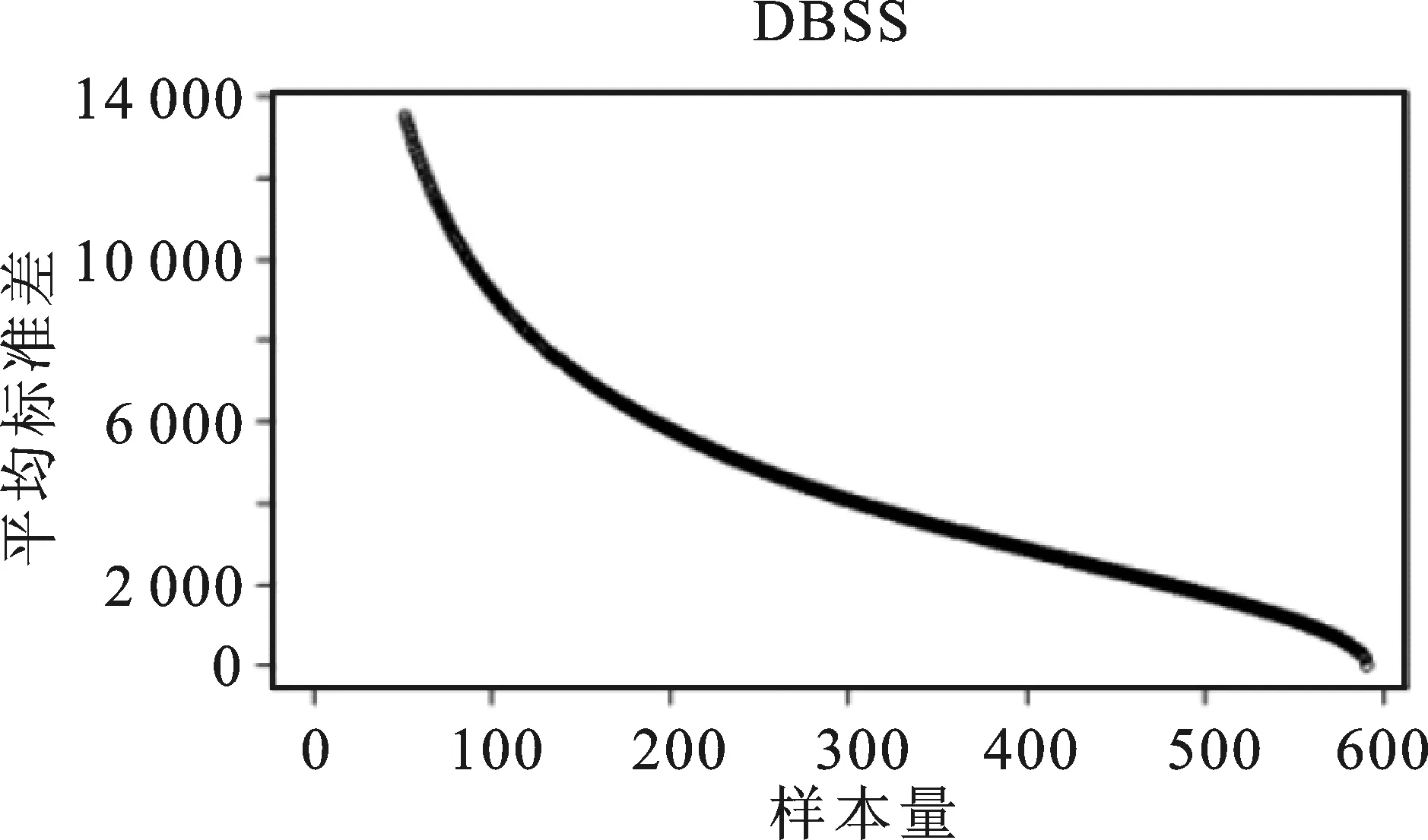
图7 三种空间平衡抽样算法估计量平均标准差随样本量变动图

(三)空间平衡抽样设计降低估计量标准差的原因

以经纬度为空间辅助信息的空间平衡抽样设计之所以在估计效率方面优于传统抽样设计，主要是由于空间平衡抽样设计利用空间辅助信息获取了在空间中均匀分散的样本，削弱了总体单元之间的空间相关性对样本代表性带来的影响。传统方法获得的估计量之所以有效性较差，是由于无法在有限的样本量下保证每次进入样本的单元都能在空间上均匀分布，样本代表性无法保证。在大量重复抽样时，空间平衡抽样设计获取的样本能够保持相对稳定的特征，使用样本做出的统计推断也更加可靠。

就本案例来说，590家医院的床位数之间存在明显的空间相关性和空间聚集性，具体表现在床位数较多的大医院多数集中在中心城区，而远郊区县的医院规模普遍较小。在选取样本的过程中，传统抽样方法并未考虑到总体单元的空间位置分布，这导致每次抽样获得的样本单元空间分布情况差异较大。当大部分入样单元靠近中心城区的情况下，做出的总体总值估计可能偏大；当大部分入样单元分布在远郊区县的情况下，做出的总体总值估计可能偏小。因此，传统抽样方法面对具有空间相关性的总体时估计量的方差会偏大。空间平衡抽样设计通过总体单元之间的空间距离修改总体单元的包含概率，使空间上距离较近的单元同时入样的可能性降低，进而使每次抽样的入样单元都能在空间上尽可能的分散，获得对总体代表性更好的样本。在多次抽样时，由于每个样本中的样本单元都能够在空间中均匀地分布，因此靠近中心城区的床位数多的医院和位于远郊区县的床位数少的医院都能以尽可能接近的比例进入样本，各个样本的空间分布情况差异较小，估计效率得以提升，估计量的相对误差也随之下降。

四、结语

空间平衡抽样设计能够利用总体单元的空间位置信息调整总体单元的包含概率，抽取到在空间中均匀分布的样本，解决了空间相关性对样本代表性的影响，丰富了经济社会调查的方法体系。但是，空间平衡抽样在获得空间分布更加均衡的样本的同时，有可能给某些需要实地调查且成本较大的调查项目带来经费和人力上的挑战。如果样本单元之间的地理位置距离较远，无法集中在一个区域内集中展开调查，那么调查项目中人力和物力的投入必然随之增加。因此，空间平衡抽样设计应该考虑成本与样本代表性的权衡。另外，空间辅助信息在估计量中的使用仍有很大的研究空间，上述问题有待学者们结合实践开展进一步的研究。