驾驶机器人车辆的多模式切换控制∗

吴 俊，陈 刚

(南京理工大学机械工程学院，南京 210094)

前言

无人驾驶机器人是在危险和恶劣的环境下代替人类驾驶员进行自动驾驶操纵的工业机器人。无人驾驶机器人车辆是自动驾驶车的一种，与一般自动驾驶车辆相比，其最大的优点在于无须对车辆进行任何改装，驾驶机器人就能安装到驾驶室，实现车辆的自动驾驶，且一种驾驶机器人能适用于多种类型车辆。国外主要有德国、美国、日本等几个发达国家拥有该项技术。国内掌握该项技术的主要有东南大学、南京理工大学、南京汽车研究所、中国汽车技术研究中心等高校和研究机构[1-4]。利用无人驾驶机器人进行车辆试验获得的结果比人类驾驶员获得的结果更为精确、可靠，并可将普通车辆变为自动驾驶车辆。另外，无人驾驶机器人车辆可代替战士和武警官兵驾驶车辆，应用于部队运输、战场救援、疑兵伪装、驾车扫雷等军用领域，以及抗洪抢险、火灾救援、地震救灾和泥石流救援等警用领域。

驾驶机器人关键技术是对目标车速和轨迹的跟踪[5]。根据车辆跟踪目标工况的误差将跟踪过程分为车速误差大轨迹侧向误差小、车速误差小轨迹侧向误差小、车速误差大轨迹侧向误差大、车速误差小轨迹侧向误差大4种模式。对于多个模式的控制情况，专家和学者提出了多模式控制方法[6-7]。基于此，本文中提出了无人驾驶机器人车辆多模式切换控制方法来跟踪车速与轨迹。

陈刚等[8]利用模糊自适应PID控制方法解决了车速跟踪中调节参数的在线整定问题，但在车速误差较大时难以快速减小。Bang-Bang控制为解决这一问题提供了新思路，但单纯Bang-Bang控制输出值会上下波动，平稳性较差[9]。结合模糊 PID和Bang-Bang控制设计的模糊 PID/模糊 PID+Bang-Bang车速切换控制器，不仅控制精度高、稳定性好，而且控制响应快。

熊波等[10]运用分级模糊控制算法对车辆轨迹进行跟踪，但控制方法存在滞后性。张立广等[11]采用结合补偿控制的模糊PID跟踪算法控制转向，一定程度上解决了滞后性问题，但在轨迹侧向误差突然变大时仍需改进。相比于补偿控制，预瞄理论能更好地解决轨迹跟踪的滞后性。针对急转弯等情况，Bang-Bang控制能快速减小轨迹跟踪误差。因此，提出了基于虚拟轨迹规划的模糊PID/模糊PID+Bang-Bang转向切换控制方法来跟踪轨迹，有效地解决控制的滞后性，同时提高了控制的响应速度。

本文中提出了一种无人驾驶机器人车辆多模式切换控制方法。建立了驾驶机器人加速、制动机械腿和转向机械手运动学模型和车辆动力学模型，设计了加速/制动机械腿切换控制器、模糊PID/模糊PID+Bang-Bang车速切换控制器和模糊PID/模糊PID+Bang-Bang转向切换控制器，实现了驾驶机器人对车辆加速、制动和转向的协调控制，最终实现了对车速与轨迹的精确跟踪。

1 系统结构

驾驶机器人结构如图1所示，主要由离合/制动/加速机械腿、换挡/转向机械手、驱动电机及控制系统组成。加速、制动和离合机械腿能操纵各种车型的加速、制动和离合踏板。换挡机械手既能完成手动挡车型的换挡任务，也能完成自动挡车型的挡位变换。由于自动挡车辆基本在D挡行驶，所以文中没有考虑其换挡模型。

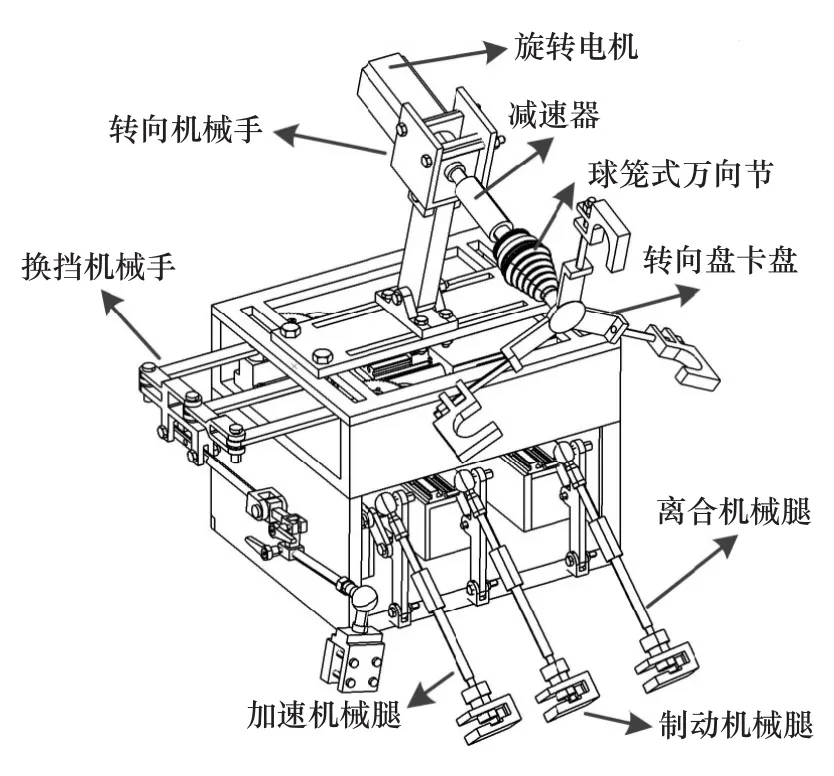
图1 驾驶机器人结构

2 驾驶机器人车辆模型

2.1 车辆动力学模型

汽车在平路上行驶主要受力包括驱动力、制动力、滚动阻力、空气阻力和加速阻力。加速和制动时车辆动力学模型为

式中:m为车辆总质量；f为滚阻系数；CD为空阻系数；A为迎风面积；ux和ax分别为纵向车速和加速度；Ft和Fxb分别为驱动力和地面制动力。

车辆横向动力学模型采用2自由度车辆模型，其状态空间方程为

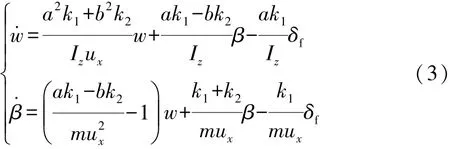
式中:w为车辆横摆角速度；β为车辆质心侧偏角；Iz为车辆绕z轴转动惯量；k1，k2分别为前后轮侧偏刚度；δf为前轮转角；a，b分别为前后车轴到质心的距离。

2.2 转向机械手运动学模型

转向机械手旋转电机产生转角θm，经减速器、球笼式万向节和转向盘卡盘传到转向盘的转角为θs，从而产生前轮转角δf。将转向机械手的传递函数A1(s)简化为低阶环节，即

式中:T1为时间常数，表示转向响应的快慢；k为转向角增益。

2.3 驾驶机械腿运动学模型

加速机械腿与制动机械腿采用相同结构，因此只须分析其中一种。驾驶机械腿运动学模型如图2(a)所示。其中，汽车踏板简化为摇杆l5，驾驶机械腿与踏板连接处为旋转副，并将图2(a)模型分解为图2(b)的左半部分和右半部分。

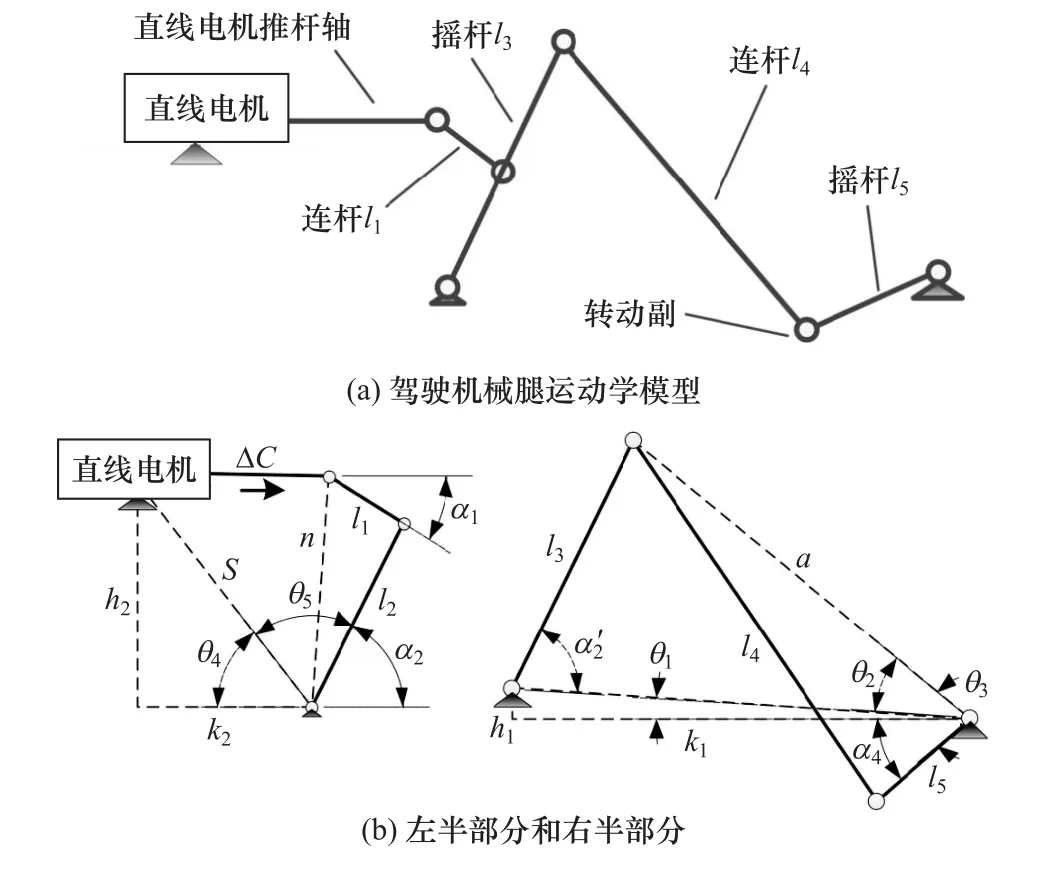
图2 驾驶机械腿运动学模型

运用D-H法建立驾驶机械腿运动学模型较复杂。此处利用驾驶机械腿各杆长度和杆间角度的关系，得出电机输出位移ΔC和α4的关系，即

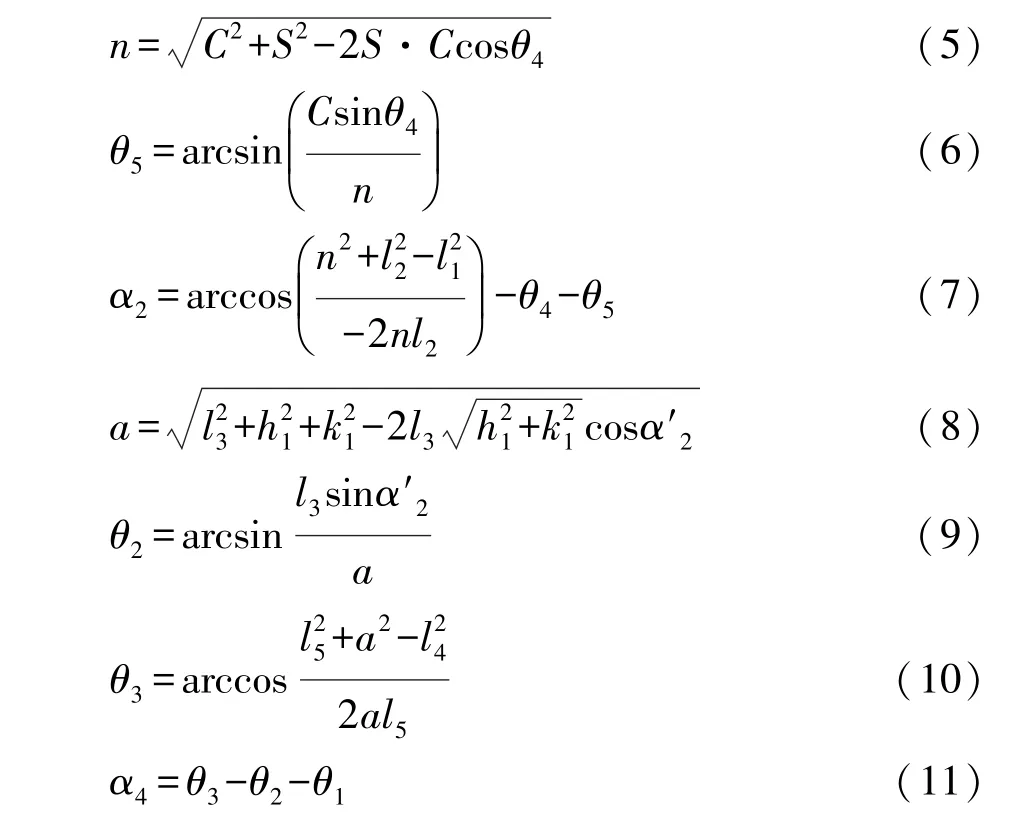
式中:h1，k1，h2，k2，S，θ1，θ4均为已知的驾驶机器人安装参数；C为直线电机推杆轴总长，ΔC＝C-C0，C0为初始时刻直线电机推杆轴长度；l1～l4为机械腿结构尺寸，l2从l3中分离出来，为 l3的1/2；l5为踏板模型长度；α4为踏板与水平线夹角。

由式(5)～式(11)所述的各变量之间的关系，可以推得ΔC和α4之间的关系，即f(ΔC)＝α4。

2.4 驾驶机械腿产生的驱动力和制动力

加速机械腿直线电机输出位移ΔC，使α4变化，从而产生节气门开度αt。节气门开度αt和驱动力Ft的关系为

式中:τ为发动机时间常数；kα为节气门开度与驱动力的比例系数；αt为节气门开度。在αt和Ft间增加一低阶环节A2(s)来表示加速迟滞现象。该低阶环节分析与转向机械手类似。

对装有鼓式制动器的车辆，制动机械腿直线电机输出位移ΔC，使α4变化，继而产生制动主缸活塞位移xz和制动轮缸活塞位移xl。制动主缸活塞位移xz与输入力Fin的关系为

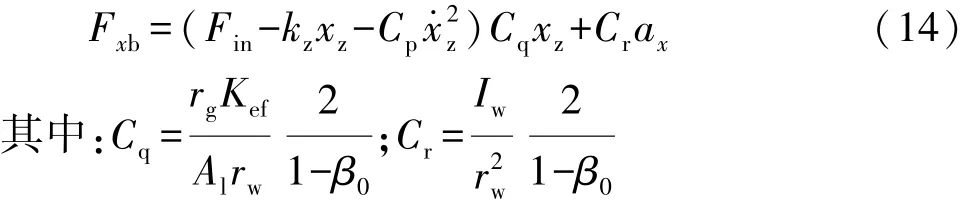
式中:rw和rg分别为车轮和制动鼓半径；Iw为车轮转动惯量；Kef为制动效能因素；β0为制动器制动力分配系数。kl和 Al的乘积数值上等于轮缸推力Fpu。

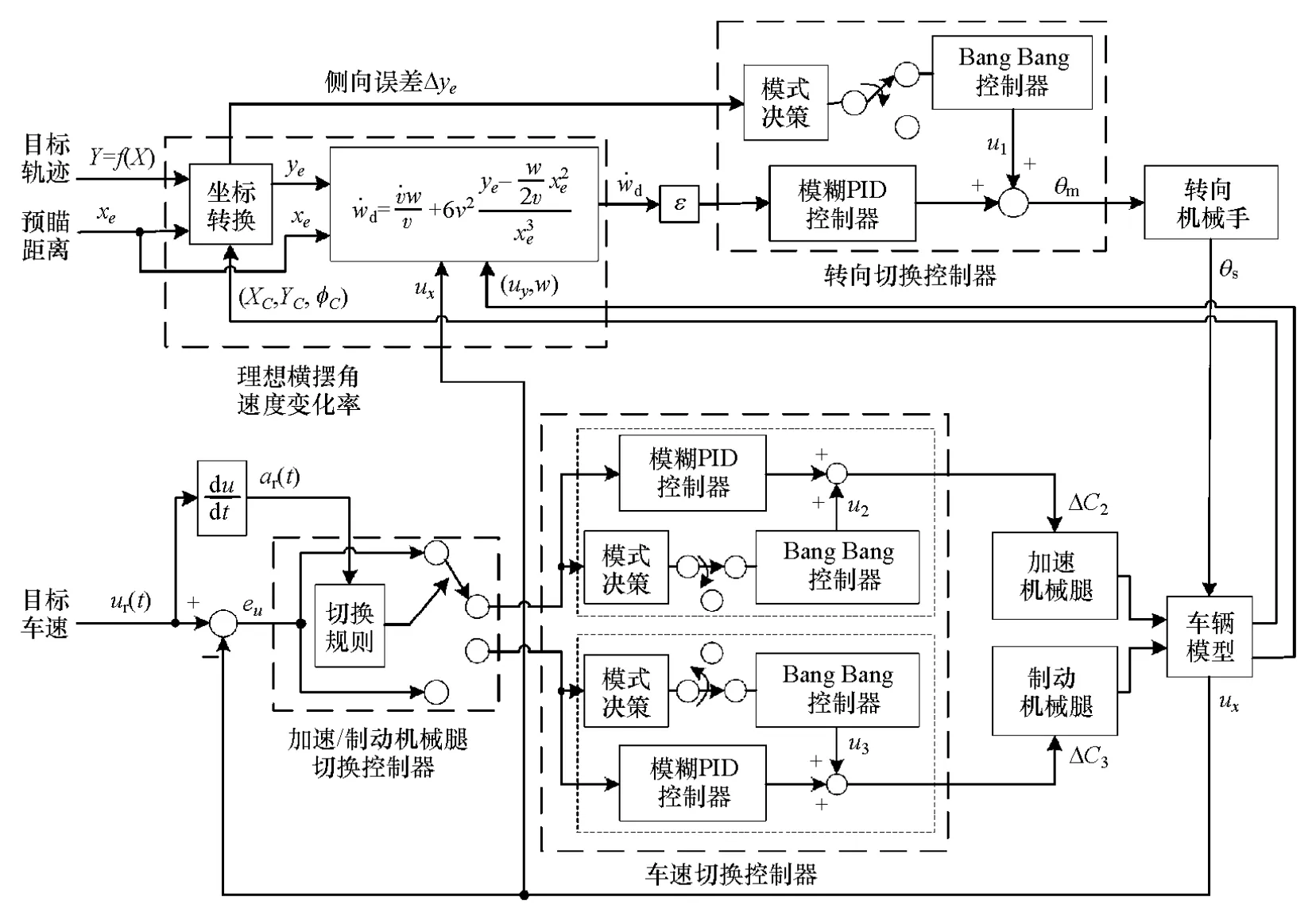
图3 驾驶机器人车辆多模式切换控制系统

3 多模式切换控制方法

驾驶机器人车辆多模式切换控制系统框图如图3所示，主要由车辆模型、理想横摆角加速度产生模块、加速/制动机械腿切换控制器、模糊 PID/模糊PID+Bang-Bang车速切换控制器和模糊PID/模糊PID+Bang-Bang转向切换控制器组成。其中，车速切换控制器以车速误差eu为模式决策和模糊PID控制器的输入，输出驾驶机械腿直线电机位移ΔC2和ΔC3。转向切换控制器以轨迹侧向误差Δye为模式决策，以当前时刻与下一控制时刻的横摆角速度之差εw·d为模糊PID控制器输入，输出旋转电机转角 θm。

3.1 理想横摆角加速度

在车辆当前位置与预瞄点之间实时规划一条逼近目标轨迹的虚拟轨迹，可将轨迹跟踪转换为对下一控制时刻横摆角速度的跟踪[12]。

车辆坐标系转换见图4，OXY为大地坐标系，OCX1Y1为车辆局部坐标系。在坐标系OXY中，车辆质心坐标为(XC，YC，φC)，预瞄点 OP坐标为(XP，YP，φP)，φC和φP分别为车辆在OC和OP处时，车辆纵轴线与大地坐标系横坐标的夹角。坐标系OCX1Y1中 OP坐标(xe，ye，φe)为

式中:xe为预瞄距离；ye为坐标系OCX1Y1中车辆当前位置与预瞄点侧向偏差；φe为方位偏差。坐标系OCX1Y1中，实时规划虚线轨迹方程为

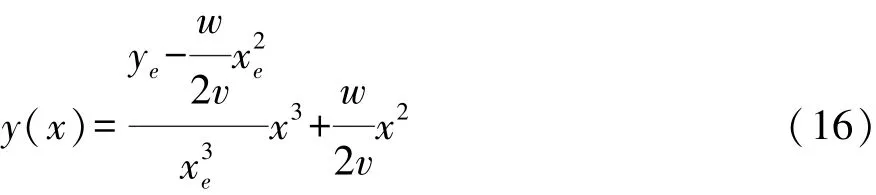
式中:w，v分别为当前车辆质心横摆角速度和车速。继而可得车辆沿此虚拟轨迹行驶时，当前横摆角加速度和下一控制时刻的横摆角速度wr:

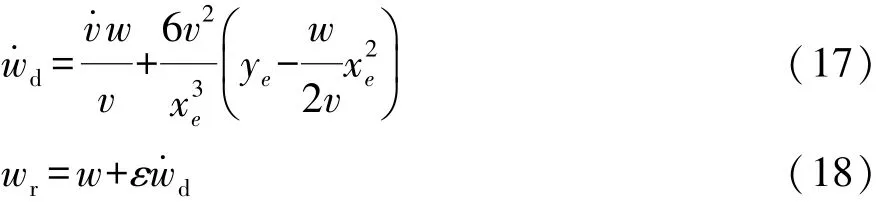
产生的地面总制动力Fxb为

式中ε为与控制的间隔时间相关的比例系数。

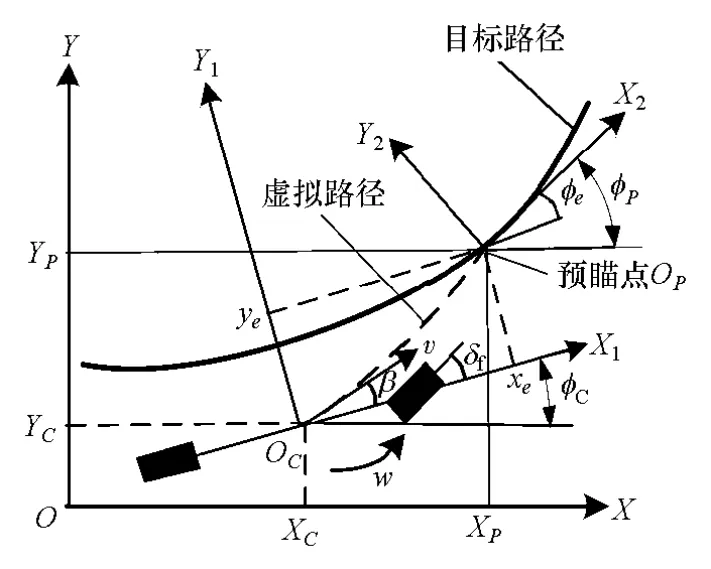
图4 车辆坐标系转换

3.2 加速/制动机械腿切换控制器

一般情况下，加速踏板与制动不同时作用，因此驾驶机器人加速机械腿和制动机械腿控制可设计成切换式，其切换规则设计为:当ar(t)-a0≥h时，加速机械腿控制；当ar(t)-a0＜h时，制动机械腿控制。其中:ar(t)为目标车辆加速度；a0为节气门全闭时，汽车在平路上由发动机拖动转矩、滚动阻力和空气阻力产生的减速度，取-0.20m/s2；h为控制缓冲值，取0.005m/s2。

3.3 模糊PID控制器

模糊PID控制器不断检测误差e和误差变化率ec，根据模糊推理在线修改调节量 Δkp，Δki和Δkd。 变量 e，ec，Δkp，Δki和 Δkd的模糊论域均设为{-6，-4，-2，0，2，4，6}，模糊子集均为{NB，NM，NS，ZO，PS，PM，PB}，并用量化因子将模糊论域分别调节到与车速误差与横摆角速度误差相适应的范围。变量采用的隶属度函数如图5所示。模糊PID控制器的模糊控制规则在已有专家经验[8]的基础上进行修正建立。由于车速与转向控制中，模糊推理对调节量Δkp，Δki和Δkd的在线修正具有相似性，故转向机械手和加速/制动机械腿的模糊PID控制器采用相同的模糊控制规则，如表1～表3所示。文中采用Zadeh模糊逻辑进行and操作，并采用质心法去模糊化。

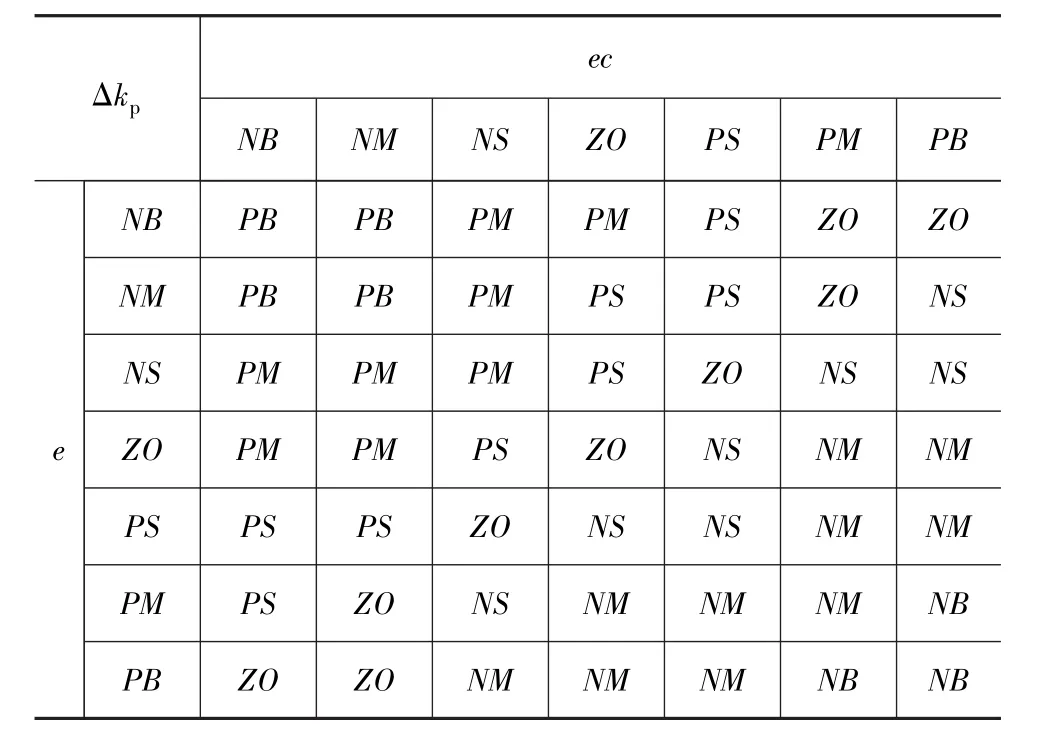
表1 Δk p的模糊规则

表2 Δk i的模糊规则

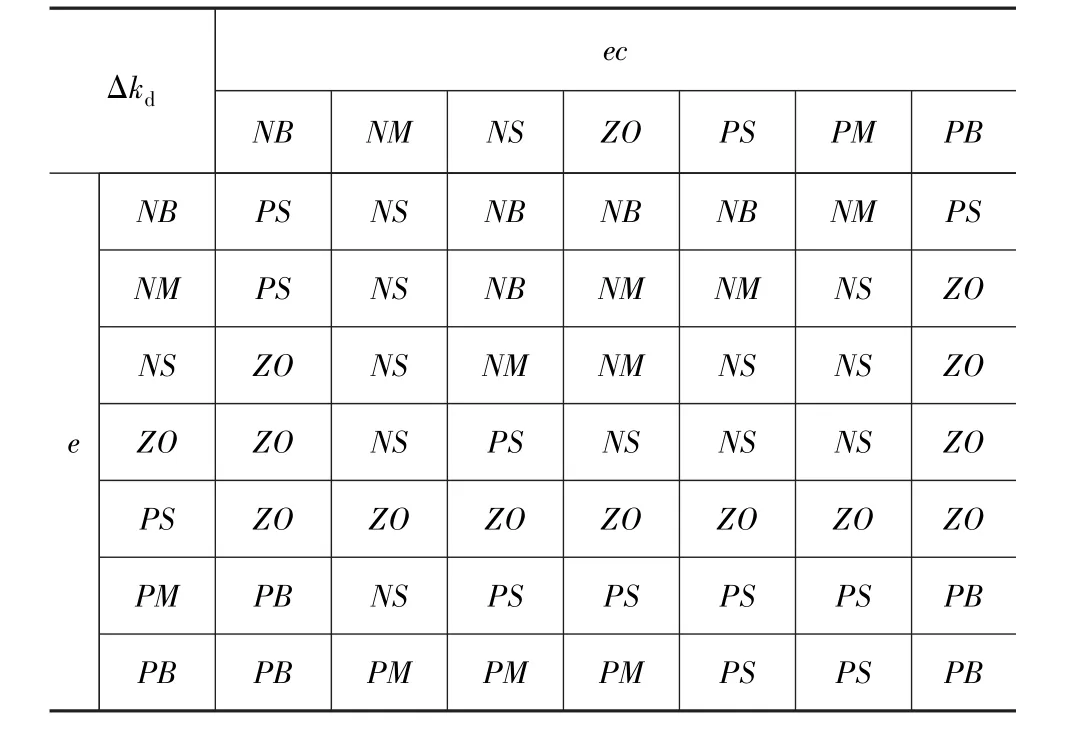
表3 Δk d的模糊规则

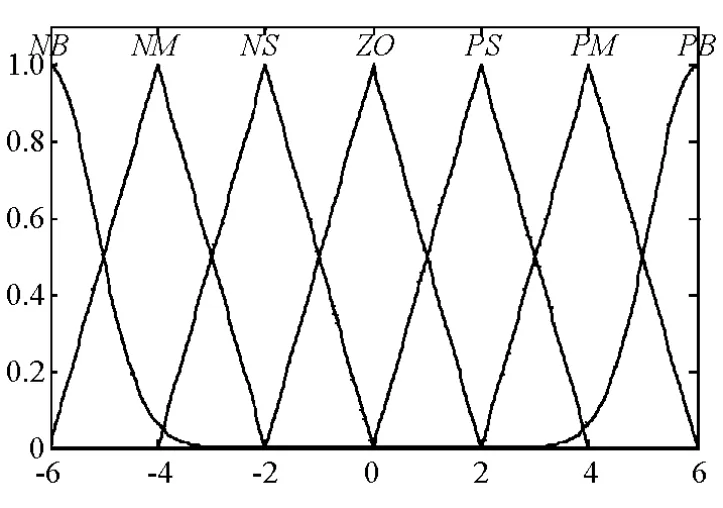
图5 隶属度函数

3.4 Bang-Bang控制器与多模式切换控制规则

模糊PID控制器始终参与系统控制，只有Bang-Bang控制器存在开闭间的切换。Bang-Bang控制器的控制规则为

式中:uk为控制器的输出值；umax和umin分别为控制器输出的最大正值和最大负值；ek为模式决策的输入；Ek为模式决策的临界值。

模式划分示意图见图6，车辆跟踪多模式由4种模式组成:①车速误差大轨迹侧向误差小；②车速误差小轨迹侧向误差小；③车速误差大轨迹侧向误差大；④车速误差小轨迹侧向误差大。

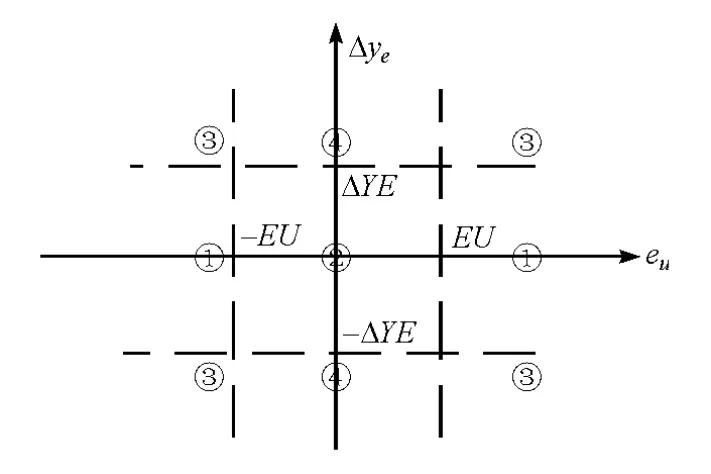
图6 模式划分示意图

结合Bang-Bang控制器的控制规则，多模式切换控制规则为

式中:eu和Δye分别为车速误差和轨迹侧向误差；EU和ΔYE分别为车速和转向的模式决策临界值；u1，u2和u3分别为转向机械手、加速和制动机械腿Bang-Bang控制器输出；U1，U2和 U3分别为 Bang-Bang控制器输出相关值。

4 仿真与试验验证

为验证该方法的有效性，进行了仿真和试验。仿真在Matlab/Simulink上进行，采用本文方法和模糊PID方法分别控制驾驶机器人车辆完成排放耐久性试验的车速跟踪仿真和双移线仿真。试验包括PID控制驾驶机器人车辆和人类驾驶员车辆的底盘测功机排放耐久性试验和双移线试验。驾驶机器人车辆试验根据相关标准[13]，在BOCO NJ 150/80型底盘测功机上由驾驶机器人对长安悦翔自动挡轿车进行长时间的排放耐久性试验，部分试验现场见图7。人类驾驶员车辆的排放耐久性试验参见文献[14]，记录车速变化。由于驾驶机器人车辆未安装定位装置，故目前无法利用驾驶机器人完成双移线试验。根据相关文献[15]，在交通部公路交通试验场由人类驾驶员对桑塔纳某型号轿车进行双移线试验。试验中，由驾驶员操纵车辆，2名试验员随车实时采集测试数据。部分关键仿真参数如表4所示。

图7 驾驶机器人车辆进行排放耐久性试验

表4 关键仿真参数

图8 0～48km/h的车速跟踪试验与仿真曲线对比

图9 为车速在50km/h时双移线试验与仿真曲线对比，包括人类驾驶员车辆试验曲线、本文方法和模糊PID分别控制驾驶机器人车辆仿真曲线。由图9(a)可见，试验与仿真曲线的变化趋势基本吻合，表明了本文方法的合理性。人类驾驶员操纵车辆进行试验得到的试验误差较大，尤其在X＝40m的弯道之后，这是因为人类驾驶员由于心理和反应滞后因素，很难精确跟踪弯道轨迹。由图9(b)可见，除X＝40，75，120，155m 4处之外，本文方法比模糊 PID 控制精度高，将轨迹侧向误差控制在±0.05m内。因X＝40，75，120，155m 4处为预设双移线轨迹的折线拐角，故该4处的侧向误差很小，且两种方法几乎一样。

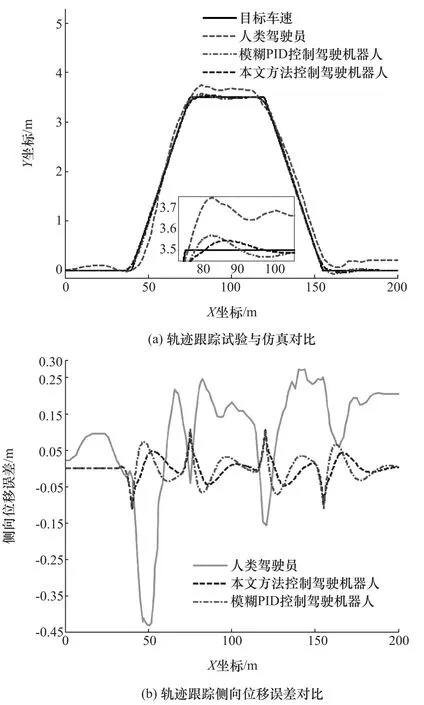
图9 50km/h的双移线工况下轨迹跟踪试验与仿真对比曲线

5 结论

提出一种无人驾驶机器人车辆多模式切换控制方法。建立了驾驶机器人加速、制动机械腿运动学模型、转向机械手运动学模型和车辆纵横向动力学模型，并设计了模糊PID/模糊PID+Bang-Bang车速

图8为0～48km/h排放耐久性试验与仿真曲线对比。由图8(a)可见，人类驾驶员完成车速跟踪的结果很不理想。这是因为长时间跟踪车速循环工况，人类驾驶员会产生身心疲劳，很难把握每个工况循环的开始时刻，且车速波动大。PID控制驾驶机器人比人类驾驶员得到的试验结果要好，但仍没有达到试验要求。采用本文方法与模糊PID方法的车速跟踪仿真跟踪误差较小，在±2km/h以内，均满足试验要求。但采用该方法控制，当跟踪误差超过切换临界值时，Bang-Bang控制的加入使跟踪误差快速减小(图8(b)局部放大图)，从而得到比模糊PID控制更精确的结果。切换控制器、模糊PID/模糊PID+Bang-Bang转向切换控制器和加速/制动机械腿切换控制器，并进行了仿真与试验验证。

车速跟踪试验与仿真表明了本文方法能在模糊PID稳定跟踪控制的基础上，进一步将车速误差快速减小到±1km/h以内，满足车速跟踪试验要求。人类驾驶员双移线试验与本文方法仿真曲线变化趋势基本吻合，表明了该方法能实时在车辆当前位置与预瞄点之间规划一条虚拟轨迹，合理地跟踪下一控制时刻的横摆角速度，在模糊PID稳定跟踪的基础上，能利用Bang-Bang控制进一步快速减小轨迹侧向误差。

今后将考虑无人驾驶机器人车辆模型简化带来的误差，对本文中提出的控制系统稳定性进行理论证明，解决控制方法在车速和转向控制的实时性问题，并进行驾驶机器人车辆室外道路的试验研究。