重叠网格隐式挖洞方法的改进与应用

江维青，杨爱明

(复旦大学 航空航天系，上海 200433)

在计算流体力学领域，针对结构复杂的几何体生成高质量的单块网格比较困难，而重叠网格技术[1]则是针对几何体的各个部件分别生成单块网格，各部件网格之间可以任意相交，重叠区域的网格单元经过预处理后再从其他网格块中插值获得流场信息.因为每一网格块的拓扑结构简单，重叠网格方法大幅降低了复杂外形网格生成的难度.该方法在过去的30年里被广泛应用于航空航天飞行器流场的数值模拟，并在近些年延伸到用于模拟风力发电机[2]、水下潜航器[3]和直升机全机[4]等复杂流场.

在重叠网格的预处理过程中，需要将重叠区域的网格单元分为计算单元、插值单元与非计算单元，这一过程也被称为“挖洞”.传统的挖洞方法需要识别出落在物面内部的网格单元，将它们标记为非计算单元从而形成洞区，位于洞区边界上的点则作为插值单元从其他网格块获得流场信息，再通过割补法[5]、阵面推进法[6]等方法优化洞区边界以获得更好的插值效果.

相比传统方法，由Baeder等最早提出的隐式挖洞(Implicit Hole Cutting，IHC)方法[7]则是根据网格单元质量来判断单元类型，有着自动化程度高、插值区域网格匹配度好等优点，是目前较受关注的重叠网格挖洞方法之一.本文针对隐式挖洞方法的特点进行了研究与改进，选择物面距与网格体积的乘积作为网格单元质量判断标准，增加识别物面内网格单元与去除多余插值单元的步骤，通过建立网格块挖洞优先级矩阵以及基于模板跳跃法的搜索方法提高了贡献单元搜索效率，并以复杂飞行器构型的重叠网格生成与流场计算对本文发展的方法进行了验证.

1 隐式挖洞方法简介

隐式挖洞方法的核心是一个基于网格单元质量做选择的过程，除了给定网格本身信息之外不需要过多的人工干预.其过程可以分为两步.(1) 首先是在网格重叠区域计算所有网格单元的质量，该参数表征了一个网格单元适合成为贡献单元的程度，可以是网格单元的体积、物面距、长宽比等.(2) 然后为所有落在重叠区域内的网格搜索贡献单元，若存在质量更好的贡献单元，则该单元成为插值单元，从质量最好的贡献单元处通过三线性插值获取流场信息；若贡献单元不存在或贡献单元的质量均比该单元差，则该单元成为计算单元正常参与流场计算，这样就避免了传统方法中繁琐的洞区边界确定与调整过程.

本文中网格单元的质量选取为网格体积与物面距的乘积，其数值越小则网格质量越好.引入物面距作为质量判断标准可以有效地减少挖洞结束后孤点的数量[8]，而且靠近物面处的网格单元一般来说体积与物面距均较小，因此会被判别为高质量的计算单元，使得插值边界自然地远离了物面处流场变化梯度较大的区域，从而确保了更好的插值精度.

2 隐式挖洞方法的改进

2.1 减少计算单元与插值单元数量

原始的隐式挖洞方法仅仅通过比较网格质量区分插值单元与计算单元，不会挖去落在物体内部的非计算单元.如图1所示，绕圆形的曲线网格与均匀的笛卡尔背景网格互相重叠，以网格面积作为质量判断标准则曲线网格质量较高，背景网格相对而言质量较差.从图1可见隐式挖洞后落在圆形物面内部的背景网格被标记为计算单元，不过因为这些物面内部单元被插值单元所包围，所以其计算得到的错误信息不会传播到外界，这也是隐式挖洞方法不需要像传统方法那样识别出落在物面内部网格的原因[9].这些多余的计算单元虽然不影响计算结果的准确性，但却不利于最终的流场显示，也增加了不必要的计算量，应当采用适当的方法除去.

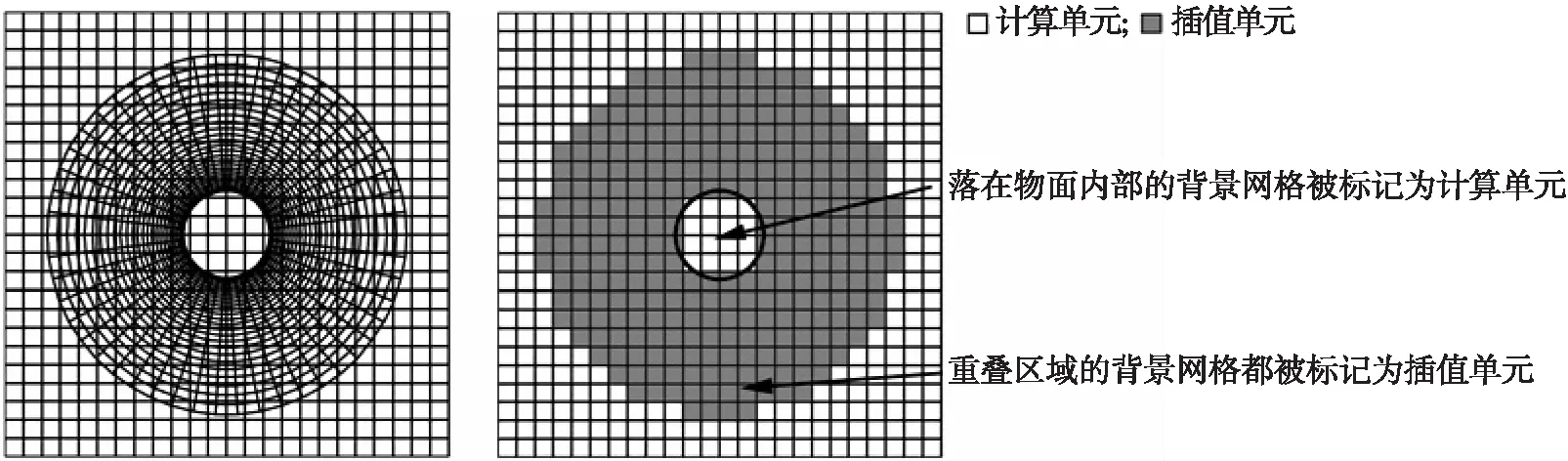
图1 原始的隐式挖洞方法结果示例Fig.1 Illustration of original implicit hole cutting method

对于落在物面内部的单元，可以在隐式挖洞开始前使用洞映射方法[10]识别并标记为非计算单元，在之后的隐式挖洞过程中即可跳过这些单元，这样虽然增加了网格预处理时的工作量，但确保了最终形成的网格不包含非必要的计算单元，也有利于流场计算结果的正确显示.

由于重叠区域所有质量较差的网格都从质量较好的网格处插值获得流场信息，原始的隐式挖洞方法最终得到的插值单元数量较大，而其中的许多插值单元并非必要.针对这一问题可以采用如下措施进行改进： 网格质量较差的单元不再全部被标记为插值单元，而是先统一标记为非计算单元，再根据计算方法所需要的插值边界层数进行修正，将与计算单元相邻的若干层非计算单元转变为插值单元即可.图2展示了应用上述优化步骤后的绕圆形网格与背景网格隐式挖洞结果，从图可见重叠区域中质量较差的的背景网格仅在边界上根据求解器需要保留两层插值单元，其余均作为非计算单元删去，再加上删去了落在物面内部的计算单元，流场计算过程中计算效率会得到相应的提升.

图2 改进后的隐式挖洞方法结果示例Fig.2 Illustration of enhanced implicit hole cutting method

2.2 提高贡献单元搜索效率

对于传统的挖洞方法，在洞边界确定后只需要为所有插值单元搜索贡献单元即可，而对于隐式挖洞方法，需要对所有位于重叠区域的网格单元执行搜索贡献单元的流程，再与可能的贡献单元比较网格质量以确定网格单元的类型.因为搜索贡献单元的次数远高于传统挖洞方法，隐式挖洞方法在自动化程度较高的同时也有着计算量较大的缺陷.

图3 贡献单元搜索流程示例Fig.3 Illustration of donor cells searching process

为了提高贡献单元搜索效率，首先根据几何体特征建立一个关于各个网格块互相挖洞优先级的N维矩阵，N为网格块的数量.该矩阵中第n行第m列的元素表示第n个网格块是否可能为第m个网格块中网格单元提供贡献单元，1表示可能，0表示不可能.若两个网格块互相没有重叠区域，该值即为0，若两个网格块虽然互相重叠但第m个网格块的网格质量显然优于第n个网格块，例如以网格体积与物面距乘积作为质量判断标准时，机翼端部(Cap)网格质量明显优于同区域的绕机翼网格，则该值也取为0.反之若第n个网格块存在为第m个网格块中网格单元提供贡献单元的可能性，该值即取为1.搜索贡献单元之前先根据该矩阵的取值进行筛选，只在有可能存在贡献单元的网格块中进行贡献单元搜索，其余网格块直接跳过，这样可以减少许多不必要的计算量.

贡献单元的搜索方法则是基于模板跳跃法[11]发展而来.如图3所示，对需要搜索贡献单元的网格P，从某一初始单元开始，计算网格P中心点在该网格单元中的三线性插值信息，再根据等参变换获得的局部坐标决定初始单元需要向哪个方向移动以及移动的步数，如此不断循环，直到找到能包围网格P中心点的贡献单元为止，该贡献单元同时也作为下一网格搜索时的初始单元.

3 计算方法

本文中的算例均采用格心格式的有限体积法求解三维雷诺平均Navier-Stokes控制方程，其在绝对坐标系下的积分形式为：

(1)

式中：W为守恒变量；Hc和Hv为对流通量和粘性通量.其表达式为：

(2)

(2) 式中：

(3)

根据理想气体的性质，再引入以下3个方程封闭原方程组：

(4)

(2)～(4)式中：ρ为流体密度；u,v,w为流体速度在3个坐标方向上的分量；p为压强；E为单位体积的总能；H为单位体积的总焓；k为热传导系数；T和τ为温度和粘性应力；V为流体速度矢量；γ为等压比热与等容比热的比值；R为理想气体常数.

该方程的空间离散采用简单高效的Jameson中心格式，加入人工耗散项抑制数值振荡，时间离散采用鲁棒性较强的隐式LU-SSOR方法完成.湍流模型采用计算量适中的Spalart-Allmaras方程模型.物面边界为无滑移绝热边界条件，远场边界采用Riemann不变量处理.采用当地时间步长、隐式残值光顺等措施加速收敛.

4 算 例

4.1 DLR-F4翼身组合体模型

DLR-F4翼身组合体是广泛应用于现代运输飞机跨音速气动特性研究的经典模型.该模型有着丰富的风洞实验数据，被AIAA组织的第一届阻力预测工作会议选作标准研究模型.计算模型为半模，共划分为6个网格块，总网格单元数量约为5.1×106个.计算条件为： 来流马赫数Ma=0.75，雷诺数Re=3.0×106，迎角α=1.0°.

应用本文发展的隐式挖洞方法得到的重叠网格如图4所示，可见机翼网格与背景网格之间的插值边界被有效地推离了机翼表面.图5对隐式挖洞方法与传统方法进行了对比，比较两套重叠网格进行流场计算后得到的机翼展向截面压力等值线可以发现，由于隐式挖洞方法将插值边界推离了流场梯度变化较大的物面以及插值边界处网格匹配性更好，该方法得到的压力等值线过渡更光滑.

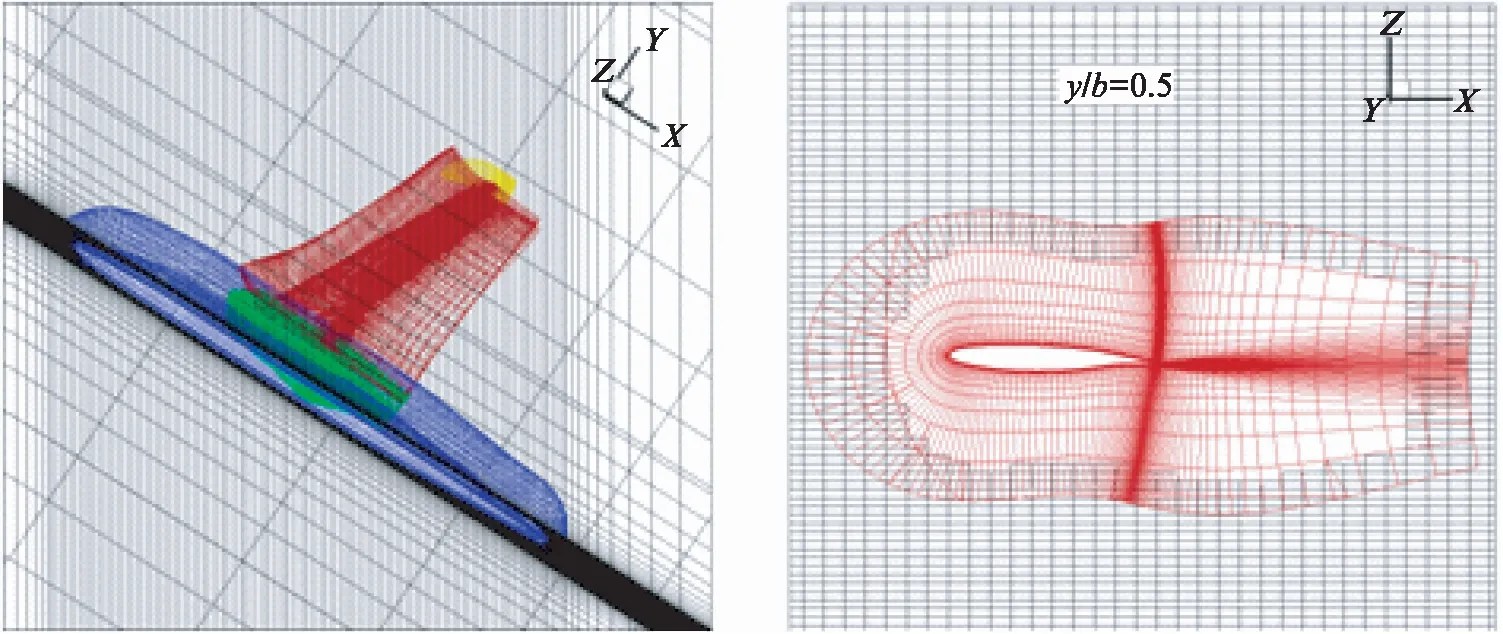
图4 应用隐式挖洞方法得到的重叠网格Fig.4 Illustration of the overset grids after implicit hole cutting method

图5 不同挖洞方法得到的压力等值线对比Fig.5 Comparison of pressure contours between different hole cutting methods

为检验计算结果的精确性，我们将本文计算结果与风洞实验数据及其他学者的计算结果[12]进行了对比.图6为机翼展向典型站位上的压力系数(CP)分布曲线，图7为升力系数曲线(CL)和阻力系数(CD)曲线，图中y/b为等y截面的y坐标与机翼展长b的比值，表明了该截面与机翼的相对位置关系，x/c为x坐标与该截面上的机翼弦长c的比值，表明了该点在机翼弦向的相对位置.从图可见本文计算结果与实验数据及其他计算结果吻合较好，本文发展的隐式挖洞方法在该算例中得到了成功应用.

图6 DLR-F4翼身组合体模型典型站位压力系数分布曲线Fig.6 CP on typical stations of DLR-F4 wing-body configuration

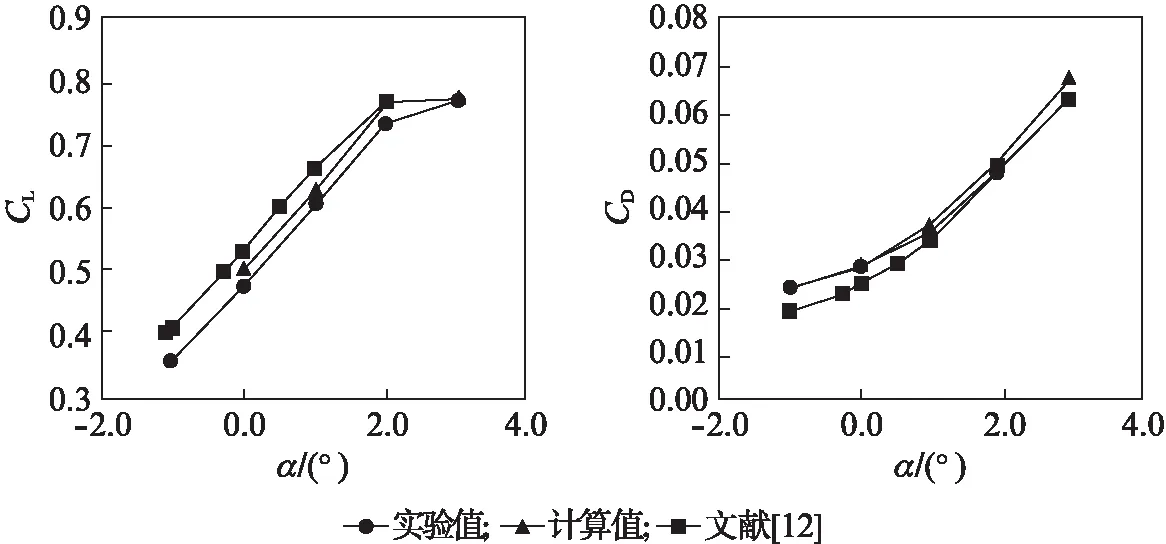
图7 DLR-F4翼身组合体模型升力系数曲线和阻力系数曲线Fig.7 Lift and drag coefficients curves of DLR-F4 wing-body configuration

4.2 NASA高升力梯形机翼模型

NASA高升力梯形机翼(NASA TrapWing)模型是专门用于验证机翼高升力构型计算能力的标准模型，其几何构型与流动机理较为复杂，有着丰富的风洞实验数据，被AIAA组织的第一届高升力预测会议选作标准研究模型.本文中使用的的是全展襟翼构型，计算模型为半模，共划分为20个网格块，总网格单元数量约为6.5×106个.计算条件为： 来流马赫数Ma=0.2，雷诺数Re=4.63×106，迎角α=13.0°.

该高升力构型主翼与前缘缝翼、后缘襟翼之间的缝道狭窄，流动现象复杂，应用本文发展的隐式挖洞方法能较好地处理缝道内各网格块交界处区域的嵌套关系，确保插值区域的网格匹配良好.图8展示了机翼展向截面y/b=0.65处的计算网格以及压力等值线，可见缝道内的压力等值线基本能光滑连续地穿越插值区域.

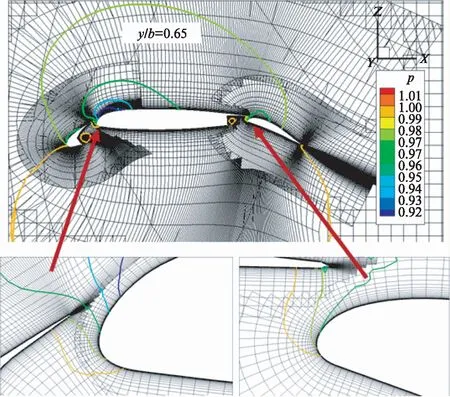
图8 机翼展向截面网格与压力等值线图Fig.8 Illustration of the overset grid and pressure contours at spanwise section

为了检验计算结果的精确性，我们同样将本文计算结果与NASA兰利研究中心的风洞实验数据及波音公司研究人员的计算结果[13]进行了对比.图9为机翼展向典型站位上的压力系数分布曲线，图10为升力系数曲线和阻力系数曲线.从图可见本文计算值与实验数据及其他计算结果吻合较好，说明本文发展的隐式挖洞方法同样在该高升力构型计算中得到了成功应用.

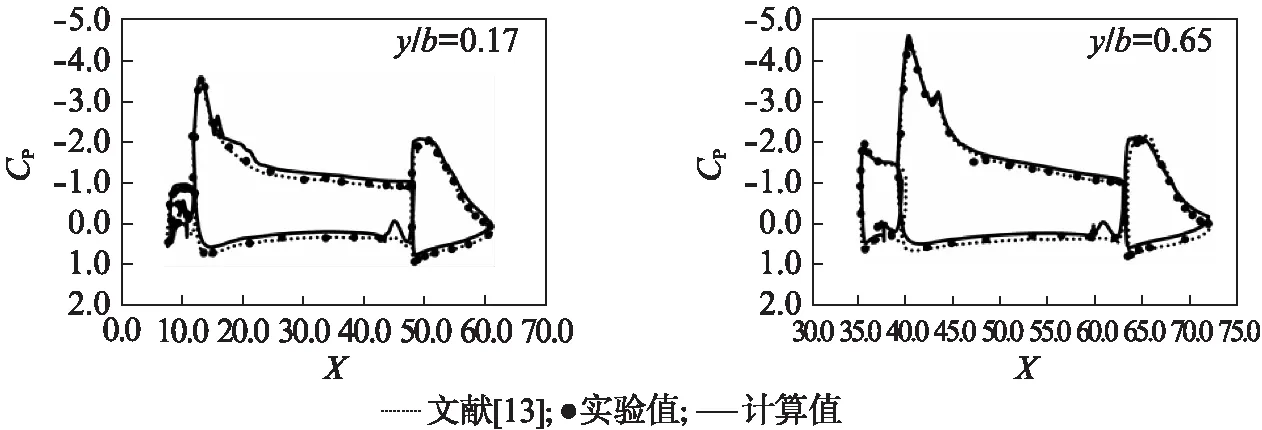
图9 高升力梯形机翼模型典型站位压力系数分布曲线Fig.9 CP on typical stations of TrapWing configuration

图10 高升力梯形机翼模型升力系数和阻力系数曲线Fig.10 Lift and drag coefficients curves of TrapWing configuration

5 结 论

本文对重叠网格隐式挖洞方法进行了改进研究，并将改进后的隐式挖洞方法应用于复杂飞行器外形重叠网格生成与流场计算，得到了以下结论：

(1) 隐式挖洞方法的核心是网格单元质量的选择，以网格体积与物面距的乘积作为质量判断标准可以有效地将插值边界推离流场变化梯度较大的物面，从而获得更好的插值效果；

(2) 原始的隐式挖洞方法自动化程度高，但由于需要不断重复贡献单元搜索流程而计算量较大，通过适当改进后可以减少非必要的插值单元与计算单元数量并提高贡献单元搜索效率，从而在保留原方法优点的基础上提高计算效率；

(3) 基于本文发展的改进的隐式重叠网格方法，我们对翼身组合体和高升力构型流场进行了数值模拟，计算结果与实验值吻合较好，网格插值边界处压力等值线光滑，说明该方法在复杂外形网格生成工作中有较高的工程应用价值.